相関係数に関する理解を深める
学部生と一緒に、竹村先生の「新装改訂版 現代数理統計学」を輪読する機会がありました。その際に分散(variance)あるいは標準偏差(standard deviation)、共分散(covariance)、相関係数(correlation coefficient)をまとめた話の内容に関して結構ウケが良かったので、そこから少し一般向けに表記を改変したものをここに置いておきます。
相関係数$ρ$は2つのベクトルの内積を考えたときのcosineの値なんですよ～という、少しググれば出てくる結論に至るまでの過程を紹介します。
準備
この手の話では準備が必要です。統計学の入門的な話をするに当たっては1つの確率変数で考えるのが普通なのですが、相関の話は2変量以上で行われる議論なので、ここでは2つの確率変数で考えます。それから、確率変数は離散型と連続型どちらで考えても、細かいところを除いては一緒なので、この記事では後者にします。
というわけで$X,Y$の2つの連続型確率変数に対して確率分布関数と確率密度関数を以下のように定義しましょう。
$F(x, y)= \int_{-∞}^{x}\int_{-∞}^{y}f(u,v)dudv$
$f(x, y)= \frac{∂^2}{∂x∂y}F(x, y)$
同時確率密度関数に関しては2つの確率変数で考えているわけだから、1つの確率変数に着目したいときには、一方をガン無視してもう一方だけを全範囲積分することもできます。その結果として周辺確率密度関数なるものが出来上がります。たとえば$x$に関して周辺を取ると
$f(x)= \int_{-∞}^{∞}f(x,y)dy$
という感じになります。確率分布関数に関しても同様に考えることができます。
同時分布と周辺分布の関係を頑張って散布図に表してみると下のようになります。同時分布は上から見たときの等高線と思ってもらって構いません。
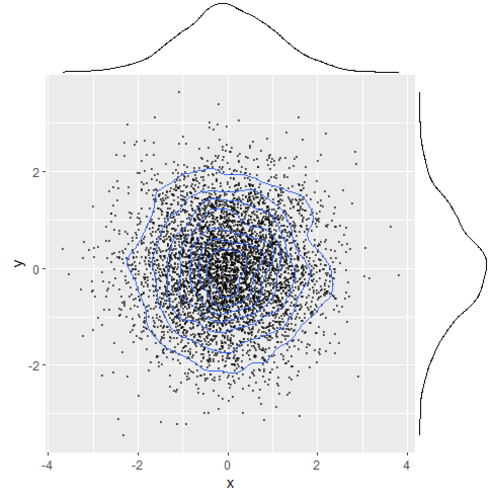scatterplot
分散の話題
統計学の入門書を見ると、$Var(X+Y)=Var(X)+Var(Y)+2Cov(X, Y) $が成り立つと書いてあることが多いです。そしてたいていの本には引き続きこんなことが書かれてあるはずです。確率変数$X,Y$が独立な場合には、$Var(X+Y)=Var(X)+Var(Y)$である、と。これはつまり、独立なときには三平方の定理が成り立つということを示しています。
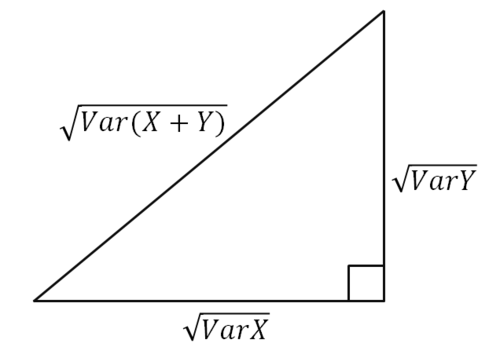var
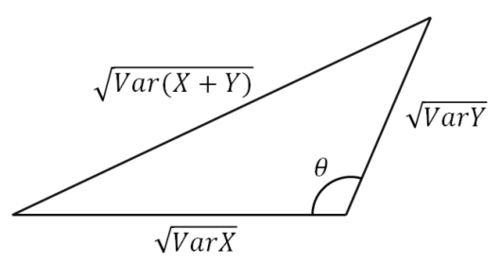
ピタゴラスの定理は余弦定理に一般化できるので、直角$Θ$に対して
$cosθ= \frac{Var(X)+Var(Y)-Var(X+Y)}{2\sqrt{Var(X)Var(Y)}}$
となって、分子が$0$になることで$cosθ$も$0$になることがわかります。ここで気づいてほしいのですが、この式の分母は標準偏差で、分子は$2Cov$と同値なので共分散です。相関係数$ρ$は$cosθ$と同じであると言われている意味が少し分かっていただけたかなと思います。
2つのベクトルが独立であれば内積は0になるという発想から、同じ結論をベクトルからも得ることができます。統計学では行列代数を多用するのですが、確率変数の直線的な関連の度合いを測るという点で、むしろベクトルの方が分かりやすいです。
では確率変数$X,Y$が独立でない場合にはどう解釈できるでしょうか。また$-1 \leq ρ \leq1$で定義されていることも確認してみましょう。簡単なのでご自身で考えてみてください。
scatterplot2
独立と相関
ここまでの議論を、準備で述べた同時確率の話に持ち込めば、次の結論が得られるでしょう。互いに互いの確率分布の情報を持たないことこそが独立であるわけだから、同時確率密度関数がそれぞれの確率密度関数の積であればよいのだと。つまり
$f_{X,Y}(x,y)=f_X(x)f_Y(y) \Longleftrightarrow f_{X|Y}(x|y)=f_X(x)$
という条件を満たせば独立であるということを示唆しているにすぎません。先の節では、$X$と$Y$が互いに独立ならばそれらは無相関であるということを示しました。しかし逆が成り立つとは限りません。相関を持たないというのは単に平衡が取れている状態なので、「実は従属的でした～！」という可能性も捨てられません。相関係数はあくまでも2変量がどれだけ近しいかを見ていて、しかもお互いの確率変数どうしを基準にみていることに注意してください。ある意味、相関と因果の違いを感じさせられる場面でもありますね。
共分散とモーメントの話題
そもそも標準偏差なんてあくまでも共分散を標準化しただけなので、実はここまでの話って茶番です。結局のところ、$ρ$を決定づけているのは共分散でしょう。共分散の話題なくして分かった気にはなれませんよね。
共分散は2つの確率変数の偏差積の平均をとったものとして紹介されていることが多いです。共分散の中でも代表的な表現方法として、以下のようなものがあります。
$\textbf{∑}=E(\textbf{X}-\textbf{EX})(\textbf{Y}-\textbf{EY})'$
は2×2対称行列かつ非負定値行列で、その対角要素は確率変数の分散である。
この分散共分散行列は、分散の概念を拡張したものと解釈できます。しかしこの概念が突然出てくると少し難しく感じるので、モーメントを用いてもう少し掘り下げてみようと思います。
・原点まわり$(j,k)$次のモーメント
$μ_{jk}=\int_{-∞}^{∞}\int_{-∞}^{∞}x^jy^kf(x,y)dxdy$
・平均まわり$(j,k)$次のモーメント
$ν_{jk}=\int_{-∞}^{∞}\int_{-∞}^{∞}(x-μ_{10})^j(y-μ_{01})^kf(x,y)dxdy$
ここで$μ_{10}$は$X$の1次モーメント、$μ_{01}$は$Y$の1次モーメントを表す。
これを用いると、共分散は以下のように定義できます。
共分散は平均まわり$(1,1)$次のモーメントで、
$Cov(X,Y)=ν_{11}=μ_{11}-μ_{10}μ_{01}\\
=E(XY)-E(X)E(Y)\\
=E(X-EX)(Y-EY)$
定義3と定義4をもとに、定義2にある分散共分散行列を変形すると、
$∑= \begin{eqnarray}
\left(
\begin{array}{cc}
ν_{20}^2 & ν_{11} \\
ν_{11} & ν_{02}^2
\end{array}
\right)
\end{eqnarray}
$$=$$
\begin{eqnarray}
\left(
\begin{array}{cc}
σ_1^2 & ν_{11} \\
ν_{11} & σ_2^2
\end{array}
\right)
\end{eqnarray}$
となります。ここで$σ_1^2$は$X$の分散を、$σ_2^2$は$Y$の分散を表しています。
ここまでの記法を$ρ$に適用すれば、以下のようになります。
$ρ= \frac{v_{11}}{\sqrt{v_{20}^2v_{02}^2}} = \frac{v_{11}}{σ_{1}σ_{2}} $
さいごに
分散の個所に関しては高校生にも参考にしてもらえるよう、マイルドな表現にしてみました。とにかくここら辺のトピックはさまざまな話に展開しやすく、皆が一度は苦しむであろう自由度の説明にはもってこいですし、独立性と無相関性の個所は行列代数を用いてもう少し丁寧に追いたかった個所です。最低限の理解ということで分散共分散行列に関しては深掘りしませんでしたし、主に2変数に限定していたり、細かいところや途中計算を省いている個所もあります。時間が許されるならば追記なり新規で記事を書こうかなあと思っています。
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
