自作問題解説2
僕がtwitterに載せた自作問題です
https://twitter.com/Gnu_yshys0624/status/1351106166651281409?s=20
三角形ABCで、角ABC = 45°である。ACの中点をM、三角形ABCの外心をOとする。AB² - BC² = 8のとき、三角形BOMの面積を求めよ。
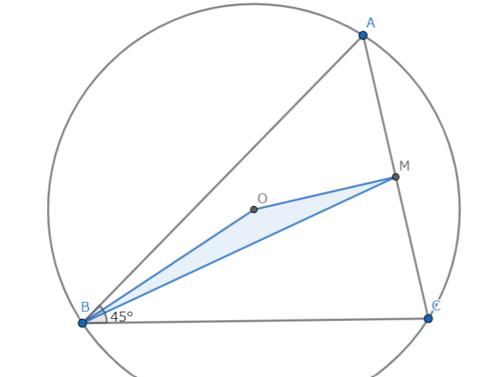 図1
図1
解説
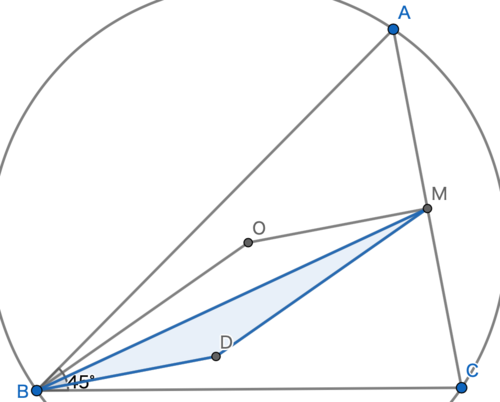 図2
図2
四角形BDMOが平行四辺形となるように点Dをとる。このとき
$\triangle{BDM}$と$\triangle{BOM}$の面積は等しい。
ここで、$OM/\!/BD,OM\perp MC,MC = OM = BD$より
$BD\perp MC,BD = MC$である。
ここで、四角形BCMDを4つ図のように繋げると大小二つの正方形ができる。(記号は対応していません)
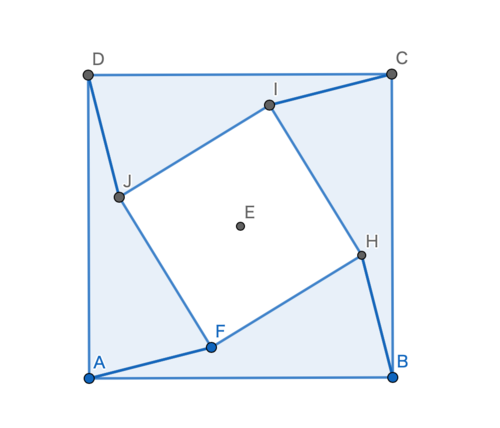 図3
図3
よって、四角形BCMDの面積は$\frac{1}{4}(BC^2 - DM^2)$と表される。
同様に、四角形ABDMの面積は$\frac{1}{4}(AB^2 - DM^2)$である。
よって四角形BCMDと四角形ABDMの面積の差は$\frac{1}{4}(AB^2 - BC^2) = \frac{1}{4}\cdot8 = 2$である。
また、(四角形BCDM) = $\triangle{BMC} -\triangle{BDM}$,(四角形ABDM) = $\triangle{BMA} + \triangle{BDM}$であり、また$\triangle{BMC} = \triangle{BMA}$であることから、四角形BCDMと四角形ABDMの面積の差は$2\cdot\triangle{BDM}$と表せる。
よって$2\cdot\triangle{BDM} = 2$より、$\triangle{BDM} = 1$
となります。
$\scriptsize{\textcolor{gray}{途中の四角形を4つ組み合わせて正方形を作るやつは初等幾何erの中ではおなじみの方法ですね}}$
