JMO2021予選 解答解説 (5~8)
本番でやらかしてしまったnoyarulerによる禊解説です。ご査収ください。
5.下図のように, 一辺の長さが $1$ の立方体 $4$ 個からなるブロックが $4$ 種類ある. このようなブロック $4$ 個を $2\times 2\times 4$ の直方体の箱にはみ出さないように入れる方法は何通りあるか. ただし, 同じ種類のブロックを複数用いてもよく, ブロックは回転させてもよい. また, 箱を回転させて一致する入れ方は異なるものとして数える.
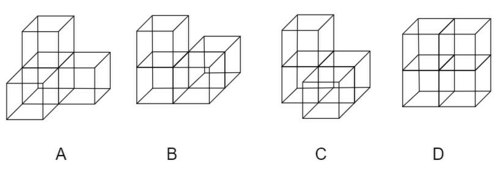jmo2021y5
答え $379$ 通り
D以外のブロックはどれも、同じブロックを $2$ つ組み合わせて $2\times 2\times 2$ の立方体の箱にはみ出さないように入れる必要がある。箱の向きを固定したとき、各ブロック $2$ つの入れ方は、A,B,C,Dそれぞれ $4$,$6$,$6$,$3$ 通りである。できた$2\times 2\times 2$ の立方体の箱をEと呼ぶことにすると、$2\times 2\times 4$ の直方体の箱にはみ出さないようにブロックを入れる方法は、E-Eの順で入れるか、または、D-E-Dの順で入れるか、の場合がある。
前者は、$(4+6+6+3)\times (4+6+6+3)=361$ 通りで、
後者は、$4+6+6+3=19$ 通りである。
前者、後者で、ともにD-D-D-Dの入れ方を数えているので、これを考慮して、求める答えは $361+19-1=379$ 通りとなる。
6.正の整数 $n$ に対して, 正の整数 $m$ であって $m$ と $n$ が互いに素であり, $m+1$ と $n+1$ も互いに素となるようなもののうち最小のものを $f(n)$ で表す.このとき, $f(1),f(2),\dots ,f(10^{10})$ のうちに現れる正の整数は何種類あるか.
答え $11$ 種類
以下、正の整数 $m$ であって $m$ と $n$ が互いに素で、$m+1$ と $n+1$ も互いに素となるという条件を単に「条件」という。
まず、$n$ を偶数とすれば、$m=1$ が条件を満たし、さらに正の整数として最小であるから、$f(n)=1$ が分かる。
次に $n+1$ が $2$ の倍数のときについて考える。$f(n)$ は $2$ の倍数であることが必要である。
$n+1$ が $3$ の倍数でないとき、$f(n)=2$。
$n+1$ が $3$ の倍数のとき、
$n+1$ が $5$ の倍数でないとき、$f(n)=2*3-2=4$。
$n+1$ が $5$ の倍数のとき、
$n+1$ が $7$ の倍数でないとき、$f(n)=2*3*5-2=28$。
$\qquad\qquad\qquad\qquad\vdots$
というように、$f(n)$ が定まる。以上の考察から、$f(n)$ として現れるのは、小さい順に、$1,2,4,28,208,2308,\dots$ となり、これらを与える最小の $n$ は、$2,1,5,29,209,2309,\dots$ である。小さい方から $n$ 番目までの素数の積を $p(n)$ とすれば、 $n\le 10^{10}$ で $f(n)$ として現れるのは、$1,2,p(2)-2,p(3)-2,\dots ,p(10)-2=6469693230$ の $11$ 種類となる。
7.三角形ABCの辺BC上に点P,Qがあり,三角形ACPの垂心と三角形ABQの垂心は一致している. AB$=10$, AC=$11$, BP$=5$, CQ$=6$ のとき, 辺BCの長さを求めよ.
ただし, XYで線分XYの長さを表すものとする.
答え $\sqrt{231}$
座標平面を用いる。
下図において、A $(0,t>0)$, B$(-\sqrt{100-t^2},0)$, C $(\sqrt{121-t^2},0)$, P $(5-\sqrt{100-t^2},0)$, Q $(\sqrt{121-t^2}-6,0)$ とし、三角形ACPと三角形ABQの垂心は $y$ 軸上の点D $(0,s)$ で一致しているとする。
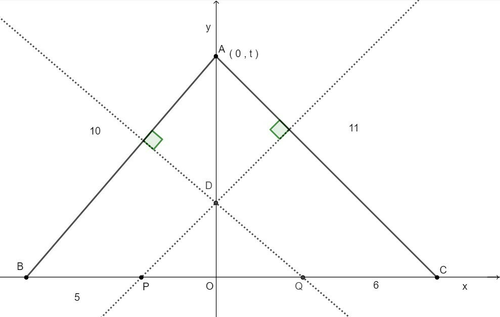jmo2021y7
AB : $y=\frac{t}{\sqrt{100-t^2}}x+t$
AC : $y=-\frac{t}{\sqrt{121-t^2}}x+t$
AB⊥DQ、AC⊥DPなので、傾きの積 $=-1$ に注意して、
DP : $y=\frac{\sqrt{121-t^2}}{t}(x-(5-\sqrt{100-t^2}))$
DQ : $y=-\frac{\sqrt{100-t^2}}{t}(x-(\sqrt{121-t^2}-6))$
DP , DQ の交点が D $(0,s)$ であるから、
$s=\frac{\sqrt{121-t^2}}{t}(\sqrt{100-t^2}-5)=\frac{\sqrt{100-t^2}}{t}(\sqrt{121-t^2}-6)$
これより、$t^2=\frac{575}{11}$
求める長さは $BC=\sqrt{121-t^2}+\sqrt{100-t^2}=6\sqrt{\frac{21}{11}}+5\sqrt{\frac{21}{11}}=\sqrt{231}$
8.$2$ 以上 $20$ 以下の整数の組 $(a_1,a_2,\dots ,a_{17})$ であって,
$a_1^{a_2^{\dots ^{a_{17}}}}\equiv a_2^{a_3^{\dots ^{a_{17}}}}\equiv 1 (\mod 17)$
となるものの個数を求めよ. ただし, 指数は右上にある $2$ 数から順に計算する.
答え $2042 \cdot 19^{14}$ 個
フェルマーの小定理から、$a_1$ と $17$ が互いに素なら、$a_1^{16}\equiv 1(\mod 17)$ である。$a_1\equiv 1$ の場合に気を付けて、次のように場合分けする。
$a_1=18$ のとき、
$\qquad a_2=18$ のとき、$a_3\dots a_{17}$ は任意。この場合、$19^{15}$ 個。
$\qquad a_2\neq 17,18$ のとき、$a_3$ が偶数で、$a_4,a_5\dots a_{17}$ は任意。この場合、$17\cdot 10\cdot 19^{14}$ 個。
$a_1\neq 17,18$ のとき、$a_2^{a_3^{\dots ^{a_{17}}}}$ が $16$ の倍数であることが必要。よって $a_2$ は $2$ の倍数。
$\qquad a_2=18$ のとき、$a_3,a_4\dots a_{17}$ は任意。この場合、$17\cdot 19^{15}$ 個。
$\qquad a_2\neq 17,18$ のとき、$a_2,a_3$ が偶数で$a_4,a_5\dots a_{17}$ は任意。この場合、$17\cdot 9\cdot 10\cdot 19^{14}$ 個。
以上あわせて、$2042\cdot 19^{14}$ 個。