2
自作問題の解答: 3次曲線と2点で接する円の軌跡
274
1
$$\newcommand{combi}[2]{{}_{#1}\mathrm{C}_{#2}}
\newcommand{disp}[0]{\displaystyle}
\newcommand{dou}[0]{\Leftrightarrow}
\newcommand{mr}[1]{\mathrm{#1}}
\newcommand{permu}[2]{{}_{#1}\mathrm{P}_{#2}}
\newcommand{vec}[1]{\overrightarrow{#1}}
$$
問題: 018
曲線: $y=x^3-x$ と2点で接する円の中心の軌跡を図示せよ。
Twitterに投稿した自作問題です。
解答
円$(x-p)^2+(y-q)^2=r^2$と$y=x^3-x$が2点で接するとき、その交点の$x$座標を$t,u$とすると、方程式$(x-p)^2+(x^3-x-q)^2-r^2=0$は$x=t,u$を重解に持つから、
$$ (x-p)^2+(x^3-x-q)^2-r^2=(x-t)^2(x-u)^2(x^2+lx+m) $$
なる恒等式が得られる。展開して係数を比較すれば、
\begin{aligned} \left\{ \begin{aligned} t^2u^2m&=p^2+q^2-r^2 \\ t^2u^2l-2mtu(t+u)&=-2p+2q \\ t^2u^2-2ltu(t+u)+m(t^2+u^2+4tu)&=2 \\ -2tu(t+u)+l(t^2+u^2+4tu)-2m(t+u)&=-2q \\ (t^2+u^2+4tu)-2l(t+u)+m&=-2 \\ -2(t+u)+l&=0 \end{aligned} \right. \end{aligned}
を得る。ここで$t+u=\alpha$, $tu=\beta$とすると、$t,u$は相異なる実数だから$\alpha^2-4\beta>0$。第5,6式より$l=2\alpha$, $m=3\alpha^2-2\beta-2$であり、第3式より
\begin{aligned} & 3\alpha^4-2\alpha^2-3\beta^2-4\beta=2 \\ \dou\quad & 3\left(\alpha^2-\frac{1}{3}\right)^2-3\left(\beta+\frac{2}{3}\right)^2=1 \end{aligned}
が$\alpha, \beta$が満たすべき条件である。ここで$\alpha^2-\dfrac{1}{3}=\dfrac{1}{\sqrt{3}\cos\theta}$, $\beta+\dfrac{2}{3}=\dfrac{1}{\sqrt{3}}\tan\theta$とおける。$\alpha^2\ge 0$より、$$ \frac{1}{\sqrt{3}\cos\theta}+\frac{1}{3}\ge 0 \dou\quad\dou -\frac{\pi}{2}<\theta<\frac{\pi}{2} $$
また$\alpha^2-4\beta>0$より
\begin{aligned} & \left(\frac{1}{\sqrt{3}\cos\theta}+\frac{1}{3}\right)-4\left(\frac{1}{\sqrt{3}}\tan\theta-\frac{2}{3}\right)>0 \\ \dou\quad & 4\tan\theta-\frac{1}{\cos\theta}<3\sqrt{3} \end{aligned}
だから$4\tan\lambda-\dfrac{1}{\cos\lambda}=3\sqrt{3}$なる$-\dfrac{\pi}{2}<\lambda<\dfrac{\pi}{2}$を用いて$-\dfrac{\pi}{2}<\theta<\lambda$。
$p,q$について、第4,5式を整理して
\begin{aligned} p&=\alpha(2\alpha^2-(3\beta+2)) \\ &=\pm\sqrt{\frac{1}{\sqrt{3}\cos\theta}+\frac{1}{3}}\left(\frac{\sin\theta(1-\sin\theta)}{\cos^2\theta}\right)=\pm\sqrt{\frac{1}{\sqrt{3}\cos\theta}+\frac{1}{3}}\left(\frac{1}{\cos\theta}\tan\theta-\tan^2\theta\right) \\ q&=\alpha((3\beta+2)\alpha^2-(3\beta+2)\beta-(3\beta+2)) \\ &=\pm\sqrt{\frac{1}{\sqrt{3}\cos\theta}+\frac{1}{3}}\left(\frac{2-3\sin\theta}{\sqrt{3}\cos\theta}+\frac{2}{3}\right)=\pm\sqrt{\frac{1}{\sqrt{3}\cos\theta}+\frac{1}{3}}\left(\frac{2}{\sqrt{3}}\cdot\frac{1}{\cos\theta}-\sqrt{3}\tan\theta+\frac{2}{3}\right) \end{aligned}
ここで、$\theta\to-\dfrac{\pi}{2}+0$の極限を考えると、$p\to\mp\infty$, $q\to\pm\infty$である。続いて$\theta\to\lambda-0$の極限を考える。
\begin{aligned} & \frac{1}{\cos\lambda}=4\tan\lambda-3\sqrt{3} \\ \therefore\,\, & 1+\tan^2\lambda=(4\tan\lambda-3\sqrt{3})^2 \\ \therefore\,\, & \tan\lambda=\frac{12\pm\sqrt{14}}{5\sqrt{3}} \end{aligned}
ここで$\tan\lambda=\dfrac{1}{4}\left(\dfrac{1}{\cos\lambda}+3\sqrt{3}\right)>\dfrac{3\sqrt{3}}{4}$から符号は正が適する。また$\dfrac{1}{\cos\theta}=\dfrac{3\sqrt{3}+4\sqrt{42}}{15}$が従う。よって、
\begin{aligned} \lim_{\theta\to\lambda-0}p&=\pm\frac{2}{25\sqrt{15}}(-22+9\sqrt{14})\sqrt{2+\sqrt{14}} \\ \lim_{\theta\to\lambda-0}q&=\pm\frac{2}{3\sqrt{15}}(-4+\sqrt{14})\sqrt{2+\sqrt{14}} \end{aligned}
一方$-\dfrac{\pi}{2}<\theta<\lambda$の範囲において、$\alpha$が正(負)のとき、$p$は単調に増加(減少)し、$q$は単調に減少(増加)する。よって求める軌跡は下図の赤線部。
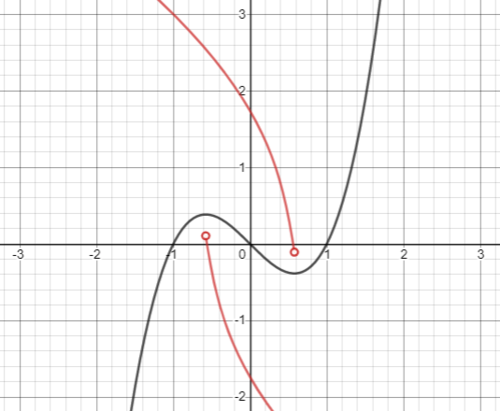Fig_018.1
ネタバレ含むコメント
解はごちゃっとしたパラメータでしか表現されないのはちょっと残念でした。きれいな表式が得られた方はご一報いただけると幸いです。この軌跡は3次関数の極値に接するように終点を迎えると想像していたので、こんな中途半端なところで途切れるのはかなり意外でした。
$p,q$が単調に増加・減少することはきちんと示すべきなのですが、あまりに計算がめんどくさく、グラフを描画させて確認するに留めてしまったのは解答を作るうえでの反省点です。
参考文献
投稿日：2021年1月31日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中