0
大学数学基礎問題
memo001 円形に並んだ数の置換
516
0
$$$$
memo-001
$N$ を $3$ 以上の整数とする. $0,1,\dots ,N-1$ を時計回りに円形に並べ, $1$ から順に時計回りに次の操作を繰り返し行う.
(操作) その数を両隣の数の和を $N$ で割った余りに置き換える.
はじめて元の数の並びと一致するのは何回の操作の後か. また, はじめて $0,1,\dots ,N-1$ の並びとなるのは何回の操作の後か.
前者の答えを $S(N)$ 、後者の答えを $T(N)$ と表すことにする。
$N=3$ の例を挙げると、
$0,1,2$
$0,2,2$
$0,2,2$
$1,2,2$
$1,0,2$
$1,0,1$
$1,0,1$
$1,2,1$
$1,2,0$
$2,2,0$
$2,2,1$
$0,2,1$
$0,1,1$
$0,1,1$
$2,1,1$
$2,0,1$
$2,0,2$
$2,0,2$
$2,1,2$
$2,1,0$
$1,1,0$
$1,1,0$
$1,1,2$
$0,1,2$
となってはじめて元に戻る。
つまり、$S(3)=24,\ T(3)=8$ である。
$3\le N\le12$ の範囲で $S(N),\ T(N)$ の値は次のようになった。
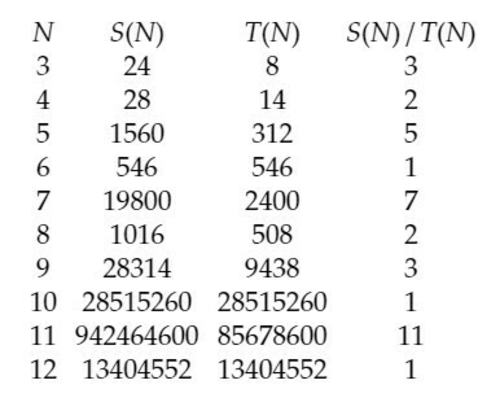 memo001a
memo001a
単調増加ではない。興味深い。
いくつか私の予想を挙げておく。(2021/02/02)
1
任意の $N$ で操作は周期的である. つまり, $S(N),T(N)$ が存在する.
2
$N$ が素数のとき, $S(N)/T(N)=N$
3
$S(N)/T(N)$ は $N$ のすべての素因数の最大公約数.
4
$S(N)$ は $N$ の約数の個数に依存する.
投稿日:2021年2月2日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中
