楕円と双曲線の双対性

455

概要

楕円とは、ある二点からの距離の和が一定の点の集合であり、双曲線とは、ある二点からの距離の差が一定の点の集合でした。しかし実は、この二つをうまく配置すると、楕円上の一点と双曲線上の一点の距離にも著しい法則を見出すことができるということを発見しました。この記事では、そのことについて説明したいと思います。

準備

この記事では、「焦点」という言葉を独特の意味で使うので、その定義をします。

焦点

楕円Eを含む空間の二点であって、楕円E上の点までの距離の和が一定であるものを、楕円Eの焦点という。また、双曲線Hを含む空間の二点であって、双曲線H上の点までの距離の差が一定であるものを、双曲線Hの焦点という。

通常の定義では、「楕円Eを含む平面の二点」であることに注意してください。そのときは焦点はただ一組に定まりますが、これを「楕円Eを含む空間の二点」にしたことで、楕円の焦点は無限に存在することになります。双曲線の場合も同様です。

さらに、平面を出たことによって、次の「反焦点」(私の造語です)というものも意味を持つようになりました。

反焦点

楕円Eを含む空間の二点であって、楕円E上の点までの距離の差が一定であるものを、楕円Eの反焦点という。

楕円を含む平面内にはこのような２点は存在しませんでしたが、空間内には存在することが後で示されます。

楕円と双曲線の双対性

本記事のゴールは次の定理です。

楕円と双曲線の双対性

楕円 $E$ : $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, z = 0$ と双曲線 $H$ : $\frac{x^{2}}{a^{2} - b^{2}} - \frac{z^{2}}{b^{2}} = 1, y = 0$ (ただし $a > b > 0$ )について、次のことが成り立つ。すなわち、 $E$ 上の異なる二点を取ると $H$ の焦点となり、 $H$ 上の異なる二点を取ると、 $E$ の焦点または反焦点となる。 $H_{1}$ を $H$ の $x < 0$ の部分、 $H_{2}$ を $H$ の $x > 0$ の部分とすれば、 $H_{1}$ から二点、あるいは $H_{2}$ から二点取るとき $E$ の反焦点となり、 $H_{1}$ と $H_{2}$ から一点ずつ取るとき $E$ の焦点となる。

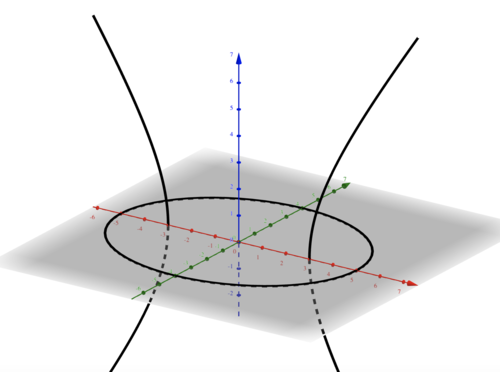楕円と双曲線

この定理の証明の核心は次の補題です。

楕円 $E$ 上の点 $e : (a \cos θ, b \sin θ, 0)$ と双曲線 $H$ 上の点 $h : (\pm \sqrt{a^{2} - b^{2}} \cosh φ, 0, b \sinh φ)$ の距離は
$a \cosh φ \mp \sqrt{a^{2} - b^{2}} \cos θ$
で与えられる。(複合同順)

$\sqrt{(a \cos θ \mp \sqrt{a^{2} - b^{2}} \cosh φ)^{2} + (b \sin θ)^{2} + (b \sinh φ)^{2}} = \sqrt{a^{2} \cos^{2} θ + b^{2} \sin^{2} θ + (a^{2} - b^{2}) \cosh^{2} φ + b^{2} \sinh^{2} φ \mp 2 a \sqrt{a^{2} - b^{2}} \cos θ \cosh φ} = \sqrt{(a^{2} - b^{2}) \cos^{2} θ + a^{2} \cosh^{2} φ \mp 2 a \sqrt{a^{2} - b^{2}} \cos θ \cosh φ} = \sqrt{(a \cosh φ \mp \sqrt{a^{2} - b^{2}} \cos θ)^{2}} = a \cosh φ \mp \sqrt{a^{2} - b^{2}} \cos θ$

このように、楕円 $E$ 上の点と双曲線 $H$ 上の点の距離は、きれいに平方根が外れて、 $θ$ に依存する項と $φ$ に依存する項に分かれるのです。このことを用いて、定理1を証明します。

定理１

楕円 $E$ 上の点 $e : (a \cos θ, b \sin θ, 0)$ と双曲線 $H_{1}$ 上の点 $h_{1} : (- \sqrt{a^{2} - b^{2}} \cosh φ, 0, b \sinh φ)$ の距離を $f_{1} (θ, φ)$ とし、楕円 $E$ 上の点 $e : (a \cos θ, b \sin θ, 0)$ と双曲線 $H_{2}$ 上の点 $h_{2} : (\sqrt{a^{2} - b^{2}} \cosh φ, 0, b \sinh φ)$ の距離を $f_{2} (θ, φ)$ とすると、補題2より
$f_{1} (θ, φ) = a \cosh φ + \sqrt{a^{2} - b^{2}} \cos θ f_{2} (θ, φ) = a \cosh φ - \sqrt{a^{2} - b^{2}} \cos θ$
である。よって、 $i = 1, 2$ として、
$\frac{\partial^{2} f_{i}}{\partial θ \partial φ} = 0$
が成り立つ。差分の表現にすれば、
$\overset{―}{e h_{i}} - \overset{―}{e h_{i}^{'}} = \overset{―}{e^{'} h_{i}} - \overset{―}{e^{'} h_{i}^{'}}$
が任意の $e, e^{'} \in E, h_{i}, h_{i}^{'} \in H_{i}$ で成り立つということであり(ただし $\overset{―}{a b}$ は二点 $a, b$ 間の距離を表す)、これは、 $H_{i}$ から二点を取ると、 $E$ の反焦点になることを表す。また、移行して、
$\overset{―}{e h_{i}} - \overset{―}{e^{'} h_{i}} = \overset{―}{e h_{i}^{'}} - \overset{―}{e^{'} h_{i}^{'}}$
とすれば、 $E$ から二点を取ると、 $H_{i}$ の焦点となることを表す。
さらに、
$\frac{\partial}{\partial θ} f_{1} (θ, φ) = - \frac{\partial}{\partial θ} f_{2} (θ, ψ)$
が任意の $φ, ψ$ で成り立つことから、差分表現にすれば、
$\overset{―}{e h_{1}} - \overset{―}{e^{'} h_{1}} = - (\overset{―}{e h_{2}} - \overset{―}{e^{'} h_{2}})$
が任意の $e, e^{'} \in E, h_{i}, h_{i}^{'} \in H_{i}$ で成り立つ。移行して、
$\overset{―}{e h_{1}} + \overset{―}{e h_{2}} = \overset{―}{e^{'} h_{1}} + \overset{―}{e^{'} h_{2}}$
とすれば、 $H_{1}, H_{2}$ から一点ずつ取ると、 $E$ の焦点となることを表す。
以上より、定理1は示された。