パスカルの三角形の驚くべき対称性
概要
パスカルの三角形に関する面白い性質はいろいろありますが、中でもダビデの星定理という定理はとても神秘的で面白いです。そのダビデの星定理を拡張することができたので、そのお話をしたいと思います。(その時のツイートが こちら です。)
ダビデの星定理とは
ダビデの星定理とは、次の図のように、パスカルの三角形の中にダビデの星を描くように二つの正三角形を作ると、その3頂点の積が一致するというものです。
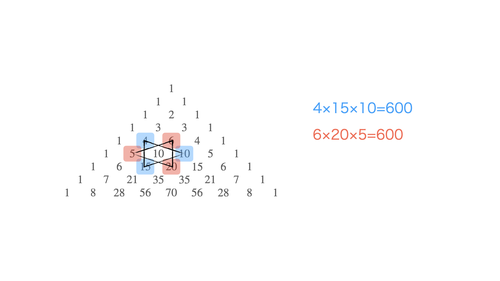ダビデの星定理
この大きさのダビデの星なら、パスカルの三角形のどの場所でも成り立つというのですから、すごい定理です。しかし、もっとすごいことが成り立つということに気がついてしまいました。
ダビデの星定理の拡張
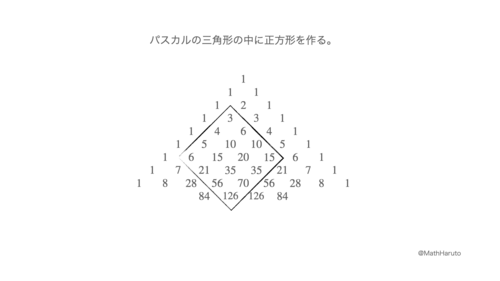
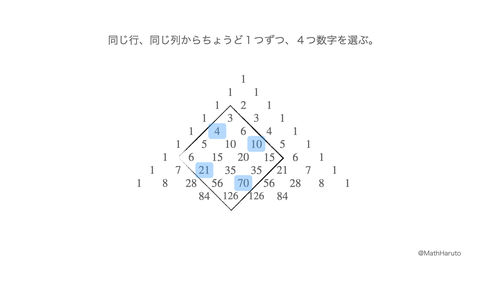
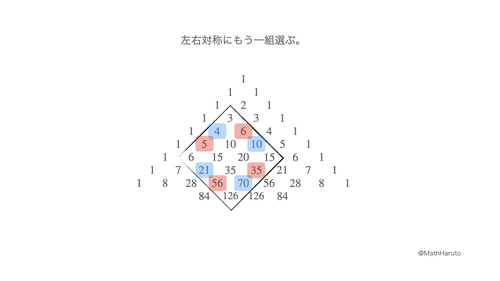
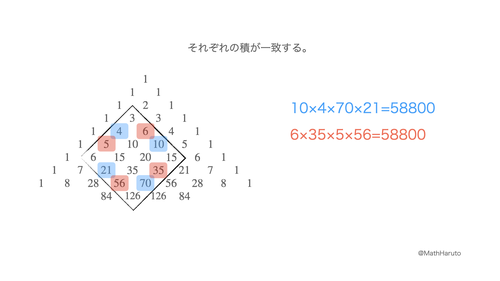
その主張は、図で見てもらった方が早いので、次の画像をご覧ください。
1
2
3
4
これを3×3の正方形で考えれば、ダビデの星定理になるので、これはダビデの星定理の拡張になっています。
本当は、さらにもう少し強いことが言えて、その主張を厳密に書けば、次のようになります。
成分を
$$
(a_{ij})=\binom{a+i+j}{b+j}
$$
に持つ$N$次正方行列$A=(a_{ij})$は、任意の正整数$n$に対して次の性質を満たす。すなわち、任意の$i_1,\cdots ,i_n\in \{1,2,\cdots ,N\}$と任意の$\sigma\in \mathfrak{S}_n$に対して、
$$
a_{i_1i_{\sigma(1)}}a_{i_2i_{\sigma(2)}}\cdots a_{i_ni_{\sigma(n)}}=a_{i_{\sigma(1)}i_1}a_{i_{\sigma(2)}i_2}\cdots a_{i_{\sigma(n)}i_n}
$$
が成り立つ。ただし、$\mathfrak{S}_n$は$n$次対称群である。
この正方行列$A$は、パスカルの三角形の$\binom{a+1}{b+1}$を頂点とする$N\times N$の正方形のことです。
$$ a_{i_1i_{\sigma(1)}}a_{i_2i_{\sigma(2)}}\cdots a_{i_ni_{\sigma(n)}}\\ =\binom{a+i_1+i_{\sigma(1)}}{b+i_{\sigma(1)}} \binom{a+i_2+i_{\sigma(2)}}{b+i_{\sigma(2)}} \cdots \binom{a+i_n+i_{\sigma(n)}}{b+i_{\sigma(n)}}\\ =\frac{(a+i_1+i_{\sigma(1)})!}{(b+i_{\sigma(1)})!(a-b+i_1)!} \frac{(a+i_2+i_{\sigma(2)})!}{(b+i_{\sigma(2)})!(a-b+i_2)!} \cdots \frac{(a+i_n+i_{\sigma(n)})!}{(b+i_{\sigma(n)})!(a-b+i_n)!}\\ =\frac{(a+i_1+i_{\sigma(1)})!(a+i_2+i_{\sigma(2)})!\cdots (a+i_n+i_{\sigma(n)})!}{(b+i_1)!(b+i_2)!\cdots (b+i_n)! \cdot (a-b+i_1)!(a-b+i_2)!\cdots (a-b+i_n)!}\\ =\frac{(a+i_1+i_{\sigma(1)})!}{(b+i_1)!(a-b+i_{\sigma(1)})!} \frac{(a+i_2+i_{\sigma(2)})!}{(b+i_2)!(a-b+i_{\sigma(2)})!} \cdots \frac{(a+i_n+i_{\sigma(n)})!}{(b+i_n)!(a-b+i_{\sigma(n)})!}\\ =\binom{a+i_{\sigma(1)}+i_1}{b+i_1}\binom{a+i_{\sigma(2)}+i_2}{b+i_2}\cdots \binom{a+i_{\sigma(n)}+i_n}{b+i_n}\\ =a_{i_{\sigma(1)}i_1}a_{i_{\sigma(2)}i_2}\cdots a_{i_{\sigma(n)}i_n} $$
上の画像の例は、$a=2,b=0,N=4,n=4,i_1=1,\cdots ,i_4=4,\sigma= \begin{eqnarray} \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 1 & 4 & 2 \end{array} \right) \end{eqnarray}$の場合です。もし、$N=4$のまま$n=3$にして、例えば$i_1=1,i_2=2,i_3=4$とすると、$4\times 4$行列の第$3$行$3$列を除いた小行列について、画像のようなことが成り立っていることになります。定理の前に、「本当はもう少し強いことが言える」と言ったのはそういう意味です。
次回予告
定理1の等式の右辺は、左辺の行成分と列成分を入れ替えたものなので、パスカルの三角形の中に作った正方行列$A$とその転置行列${}^t\!A$の間の関係とみなすことができます。次回の記事では、この関係を一般化して、同じ型の正方行列$A,B$の関係を定義し、その性質について考察したいと思います。
読んでいただきありがとうございました。
この記事を高評価した人
この記事に送られたバッジ
投稿者
