バレンタインなので、愛の形を測ってみる
バレンタインですね。今年は、コロナウィルスの影響でチョコレートをもらえないと思いますが皆さんはどうでしょうか？特に意味はないですがもう一度言います。コロナウィルスの影響でチョコレートをもらうのは厳しいと思っています。
さてそんなことより、チョコレートでハートマークを作る時、こんなことを思ったことはありませんか？
「ハートマーク作るのに最低どれくらいチョコレートいるんだろ？」と
そこで今回は、積分を使ってハートマークの方程式の面積を測ってみたいと思います。
愛の形がいろいろなように、ハートマークの表し方にも色々あるのですが、今回は、
wolframのサイト
の中から簡単に積分できるものを引っ張って計算していきます。
計算は高校生レベルで解けるので、挑戦してみてください。
1. カージオイド
まずは、高校受験等でもよく出題されるカージオイド($ r(\theta)=1-\sin\theta $)です。
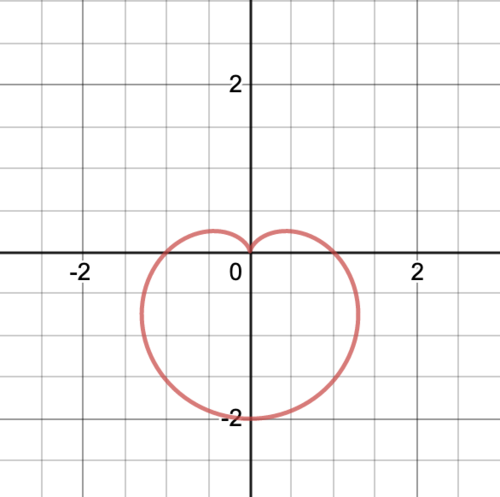カージオイド
ハートマークより少し丸みを帯びていますが、計算は簡単です。
極座標なので、
$$ \int_{0}^{2 \pi} \frac{1}{2} r^2 d\theta$$ で面積を求められます。
計算
&&&
$\int_{0}^{2 \pi} \frac{1}{2} r^2 d\theta\\ = \int_{0}^{2 \pi} \frac{1}{2} (1-\sin\theta)^2 d\theta\\ = \int_{0}^{2 \pi} \frac{1}{2} (1 - 2\sin\theta +\sin^2\theta) d\theta = \int_{0}^{2 \pi} \frac{1}{2} (1 - 2\sin\theta +\frac{1-\cos2\theta}{2}) d\theta$
$\sin$や$\cos$は$[0,2\pi]$の範囲で積分すると0になるので消すと、
$= \int_{0}^{2 \pi} \frac{1}{2}(1 +\frac{1}{2}) d\theta \\ = \int_{0}^{2 \pi} (\frac{3}{4}) d\theta = \frac{3}{4} *2\pi = \frac{3\pi}{2} $
&&&
となり、答えは$\frac{3\pi}{2}$となり大体、$4.71$くらいになります。
計算は簡単ですが、完璧なハート型ではないので、次は媒介変数表示を使ってハートマークをみていきます。
2. 媒介変数表示を使ったハートマーク
次に、
wolframのサイト
に載っているの媒介変数表示でハートマークを表していきますが、元の方程式だとでかいので
$y(0)$と$y(\pi)$との距離がカージオイドと同じ$2$になるよう縮尺して、以下のようにします。
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
y(t)=\frac{16}{11}\sin^3 t \\
x(t)=\frac{1}{11} (13\cos t-5\cos 2t-2\cos 3t-\cos 4t) \\
t \in [0,2\pi)
\end{array}
\right.
\end{eqnarray}
$$
グラフは以下になります。
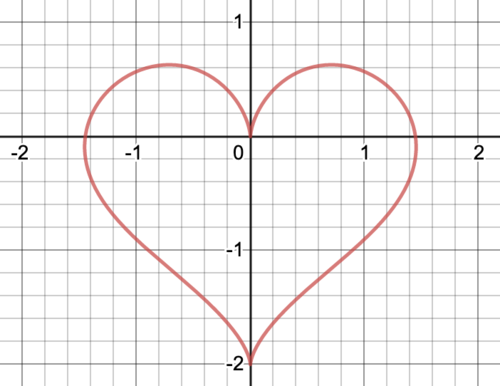ハート2
媒介変数表示なので、$x(t)$を微分して、$dx$を求め、
$$ \int_{0}^{2 \pi}y(t) x'(t)dt$$
を求めます。
また、積和の公式を使って、$cos$と$sin$の積を和に変換して積分します。
計算
&&&
$x'(t)=(\frac{16}{11}\sin^3 t)' = \frac{48}{11}\sin^2 t \cos t$
となります。
よって求める面積Sは
$\int_{0}^{2 \pi} \frac{1}{11} (13\cos t-5\cos 2t-2\cos 3t-\cos 4t)(\frac{48}{11}\sin^2 t \cos t)dt\\ =\frac{48}{11^2} \int_{0}^{2 \pi} \sin^2 t \cos t(13\cos t-5\cos 2t-2\cos 3t-\cos 4t)dt$
$\cos \alpha \cos \beta= \frac{1}{2} (\cos(\alpha+\beta)+\cos(\alpha-\beta))$となるので、
$S=\frac{48}{11^2} \int_{0}^{2 \pi} \frac{1}{2} \sin^2 t (13(\cos 2t+1)-5(\cos 3t+\cos t)-2(\cos 4t+\cos 2t)-(\cos 5t+\cos 3t))dt\\ =\frac{24}{11^2} \int_{0}^{2 \pi} \sin^2 t (13-5\cos t+11\cos 2t-6\cos 3t-2\cos 4t -\cos 5t)dt$
半角の公式$\sin^2 t=\frac{1-\cos 2t}{2}$を使って、
$S=\frac{12}{11^2} \int_{0}^{2 \pi} (1-\cos 2t)(13-5\cos t+11\cos 2t-6\cos 3t-2\cos 4t -\cos 5t)dt$
また、$\sin$や$\cos$は$[0,2\pi]$の範囲で積分すると0になるので$1\cdot13$と$-\cos 2t\cdot(11\cos 2t)$の定数部のみ考えると、
$S=\frac{12}{11^2} \int_{0}^{2 \pi} (13-11/2)dt=\frac{6}{11^2} (26-11)2\pi=\frac{180}{121}\pi$
&&&
となるので、$\frac{180}{121}\pi$となり大体、$4.67$くらいになります。
結論
3cmx3cmの正方形の上には大体$4.67cm^2$くらいのハートマークがおさまる。
明治のミルクチョコレートの情報
とH&Dによるチョコレートの密度の表を照らし合わせると、
チョコレートの密度はおよそ$1.25g/cm^3$となります。
よって、各辺が$3cm$の立方体に入るハート型のチョコレートを作るのには$17.5g$程度のチョコレートが必要
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
