文献あり

駆け足で学ぶエクスパンダーグラフ

3063

こんにちは. Le Algorithm の著者をしているのぶしみ( @knewknowl )と申します. 数学系の記事を執筆しやすそうなMathlogというサービスを知ったので, 試しがてらに一記事を執筆しようと思い立ったのでエクスパンダーグラフについての紹介記事を書いています.

グラフ理論やグラフアルゴリズム関連の研究に携わると「エクスパンダーグラフ」という単語に出会うことがあります. この記事ではこのエクスパンダーグラフについて概説します. 前提知識としては, 線形代数の基本的な事柄(固有値の定義とか)が分かっていれば大丈夫です. 念の為, 本記事の末尾に付録Aとして行列のスペクトルノルムの定義や基本的な性質を載せています.

1. 基本的な定義

基本的な用語の定義をします. グラフの隣接行列, 遷移確率行列, グラフラプラシアンの定義を知っていれば1章は読み飛ばして頂いても構いません.

有限集合 $V$ に対し, $(\binom{V}{2}) = {{u, v} \subseteq V : u \neq v}$ とします. $E \subseteq (\binom{V}{2})$ に対し, 組 $G = (V, E)$ をグラフ (graph)と呼びます (正確には有限無向グラフですが, この記事では簡単にグラフとします) ここで $E$ を辺集合, $V$ を頂点集合と呼び, それぞれの要素を辺(edge)及び頂点(vertex)と呼びます. この記事中では頂点集合のサイズを $n$ で表すことにします.

グラフ $G = (V, E)$ の各頂点 $v \in V$ に対し, $N (v) = {w \in V : {v, w} \in E}$ を $v$ の隣接頂点集合とし, $\deg (v) = | N (v) |$ を $v$ の次数(degree)と呼びます. 全ての頂点の次数が $d$ に等しいグラフを $d$ -正則グラフ( $d$ -regular graph)または単に正則グラフ(regular graph)と呼びます.

グラフ $G = (V, E)$ の隣接行列(adjacency matrix) $A \in {0, 1}^{V \times V}$ を以下で定めます:
$\begin{array}{r} A_{u, v} = {\begin{cases} 1 & if {u, v} \in E, \\ 0 & otherwise . \end{cases} \end{array}$
また, 対角行列 $D \in R^{V \times V}$ を
$\begin{array}{r} D_{u, v} = {\begin{cases} \deg (v) & if u = v, \\ 0 & otherwise \end{cases} \end{array}$
とします. また, $1 \in R^{V}$ を成分が全て $1$ のベクトルとし, $0$ でゼロベクトルを表すことにします.

$P = D^{- 1} A \in [0, 1]^{V \times V}$ で与えられる行列を $G$ の遷移確率行列(transition matrix)と呼びます. 特に, 遷移確率行列 $P$ の各成分 $P_{u, v}$ は, ${u, v} \in E$ のときは $\frac{1}{\deg (u)}$ となります. 隣接行列 $A$ は対称行列ですが, $P$ は必ずしも対称にはならないことに注意してください.

遷移確率行列という名称は, ランダムウォークに由来します. 一つの頂点から始めて隣接頂点を一様ランダムに選びそこに遷移するという確率過程をランダムウォーク(random walk) (より正確には, 単純ランダムウォーク) と言いますが, グラフ $G$ 上のランダムウォークにおいて頂点 $u$ から頂点 $v$ に移動する確率は $1 / \deg (u)$ となり, この確率を全ての $u, v \in V$ に対し行列として表現したものが遷移確率行列 $P$ になります.

$L = D - A$ で与えられる行列をグラフラプラシアン (graph Laplacian)と呼びます. また, $\tilde{L} = D^{- 1 / 2} L D^{- 1 / 2} = I - D^{- 1 / 2} A D^{- 1 / 2}$ で与えられる行列を正規化したラプラシアン (normalized Laplacian)と呼びます. ここで, $D^{1 / 2}, D^{- 1 / 2}$ はそれぞれ $D^{1 / 2} = diag (\sqrt{\deg (v_{1})}, \dots, \sqrt{\deg (v_{n})})$ , $D^{- 1 / 2} = (D^{1 / 2})^{- 1}$ で与えられる行列です.

2. スペクトルグラフ理論

グラフに付随する行列を定義しました. 実はグラフ理論には, グラフの構造的性質をその固有値を使って解析する理論があり, スペクトルグラフ理論(spectral graph theory)と呼ばれています.

2.1. 実固有値性

隣接行列とグラフラプラシアン及びその正規化はどれも対称行列なので実固有値を持ちます. 一方で遷移確率行列 $P$ は対称ではないので一見すると実固有値を持たないように見えますが, 実は $P$ の固有値は全て実数になることが示せます:

任意のグラフ $G$ に対し, 遷移確率行列 $P$ の固有値 $λ_{1}, \dots, λ_{n}$ は実数であり, $λ_{i} \in [- 1, 1]$ を満たす.

行列 $M = D^{- 1 / 2} A D^{- 1 / 2}$ を考えます. この行列は対称行列なので, 全ての固有値は実数になります. $M$ の固有値 $λ$ に対応する固有ベクトルを $x$ とします. すなわち, $M x = λ x$ が成り立ちます. ベクトル $y = D^{- 1 / 2} x$ を考えます.
$\begin{array}{r} P y = D^{- 1} A D^{- 1 / 2} x = D^{- 1 / 2} M x = λ D^{- 1 / 2} x = λ y \end{array}$
より, $P$ と $M$ は同じ固有値を持ちます.
また, Gershgorinの定理より, $P$ の全ての固有値は $[- 1, 1]$ に属し, 特に $P 1 = 1$ より $P$ は $1$ を最大固有値として持ちます.

また, グラフラプラシアン $L$ は $L 1 = 0$ より, 必ず $0$ を固有値に持ちます. 特にグラフが正則グラフのとき, $D = d I$ なので, どの行列を考えても本質的に等価です ( $I \in {0, 1}^{V \times V}$ は単位行列).

2.2. 連結性

連結性

グラフ $G = (V, E)$ を考える. 任意の二頂点 $u, v \in V$ に対して, 以下を満たす頂点の列 $(w_{0}, w_{1}, \dots, w_{l})$ が存在するとき, $G$ は連結(connected)であるという:

$w_{0} = u$ ,
$w_{l} = v$ ,
全ての $i = 0, \dots, l - 1$ に対し ${w_{i}, w_{i + 1}} \in E$ .

connectivity

直感的に言えば, どの二頂点も辺を辿って行き来できればそのグラフは連結であるということになります.

連結成分を二つ持つグラフ $G$ を考え, その連結成分のなすグラフを $G_{1}, G_{2}$ とし, それぞれの遷移確率行列を $P_{1}, P_{2}$ とします. すると $G$ の隣接行列 $P$ は, 頂点番号を適切に振り分けることで以下のブロック対角行列として表すことができます:

$\begin{array}{r} P = [\begin{array}{cc} P_{1} & O \\ O & P_{2} \end{array}] . \end{array}$
ここで $O$ は全ての要素がゼロの行列です. ベクトル $x_{1} = [1 0]^{⊤}$ と $x_{2} = [0 1]^{⊤}$ を考えると, どちらも $P x_{i} = x_{i}$ を満たすことが確認できます. なので $P$ の固有値1の多重度は $2$ になっていて, これは $G$ の連結成分の個数と等しくなります. 一般的に, 次の命題が成り立ちます.

グラフ $G$ の遷移確率行列の固有値1の多重度は, $G$ の連結成分の個数と等しい. さらにこの値は, $G$ のグラフラプラシアンの固有値0の多重度と等しい.

2.3. 二部グラフ

二部グラフ

グラフ $G = (V, E)$ を考える. $V$ の分割 $(V_{1}, V_{2})$ が存在して, $E \cap (\binom{V_{1}}{2}) = E \cap (\binom{V_{2}}{2}) = \emptyset$ とできるとき, $G$ は二部グラフ(bipartite graph)であるという.

bipartite_example

直感的に言えば, $V_{1}, V_{2}$ の間にしか辺がないような分割 $(V_{1}, V_{2})$ がとれるグラフのことを二部グラフといいます. 二部グラフの遷移確率行列は次の形で表すことができます:

$\begin{array}{r} P = [\begin{array}{cc} O & P_{1} \\ P_{2} & O \end{array}] . \end{array}$
ここで $P_{1} \in [0, 1]^{V_{1} \times V_{2}}, P_{2} \in [0, 1]^{V_{2} \times V_{1}}$ です. $V_{i}$ 内部には辺がないので, $V_{i}$ - $V_{i}$ 成分は全て $0$ になるからこのように表すことができます. ベクトル $x = [x_{1} x_{2}]^{⊤}$ を $P$ の固有値 $λ$ に対する固有ベクトルとします. このとき, $P_{1} x_{2} = λ x_{1}$ 及び $P_{2} x_{1} = λ x_{2}$ が成り立ちます. なので, $y = [x_{1} - x_{2}]^{⊤}$ に対して $P y$ を計算すると
$\begin{array}{r} [\begin{array}{cc} O & P_{1} \\ P_{2} & O \end{array}] [\begin{array}{c} x_{1} \\ - x_{2} \end{array}] = [\begin{array}{c} - P_{1} x_{2} \\ P_{2} x_{1} \end{array}] = λ [\begin{array}{c} - x_{1} \\ x_{2} \end{array}] = - λ y . \end{array}$
すなわち $y$ は $P$ の固有値 $- λ$ に対する固有ベクトルになっています! ですので, $P$ の固有値 $λ_{1} \geq \dots \geq λ_{n}$ は $0$ に関して対称的になっていて, $λ_{i} = λ_{n - i - 1}$ が成り立つことがわかります. 特に $λ_{1} = 1$ なので $λ_{n} = - 1$ です. 実は逆も成り立っており, 固有値の $0$ に関する対称性がグラフの二部性を特徴付けています:

グラフ $G$ が二部グラフであることの必要十分条件は, その遷移確率行列 $P$ の固有値 $λ_{1}, \dots, λ_{n}$ が全ての $i = 1, \dots, n$ に対し $λ_{i} = λ_{n - i - 1}$ が成り立つことである.

2.4. 例

色んなグラフに対し $P$ の固有値を見ていきましょう.

サイクルグラフ

サイクルグラフ $C_{n} = (V, E)$ は, $V = {v_{0}, \dots, v_{n - 1}}$ に対して $E = {{v_{i}, v_{i + 1}} : i \in Z / n Z}$ で定義されるグラフです (下図).

C_8 C_8

$C_{n}$ は $2$ -正則グラフで, 遷移確率行列 $P$ は
$\begin{array}{r} P_{v_{i}, v_{j}} = {\begin{cases} \frac{1}{2} & if | i - j | = 1 (\mod n), \\ 0 & otherwise \end{cases} \end{array}$
です. 少し計算は面倒ですが, 固有値を求めると $λ_{j} = \cos (2 π j / n)$ ( $j = 0, \dots, n - 1$ ) となります. $n$ が偶数のとき $C_{n}$ は二部グラフになりますが, このときこれらの固有値は $0$ に関する対称性を持ちます.

完全グラフ

完全グラフ $K_{n} = (V, E)$ は, $| V | = n$ かつ $E = (\binom{V}{2})$ となるグラフです. つまり全ての頂点対に辺があるグラフなので, $(n - 1)$ -正則です. 隣接行列 $A$ は $A = 1 1^{⊤} - I$ に対し遷移確率行列 $P$ は $P = \frac{1}{n - 1} A$ となります. 行列 $1 1^{⊤}$ は $1$ が固有値 $n$ の固有ベクトルになっていて, 他の全ての固有ベクトル $x$ は $1$ に直交するため $1 1^{⊤} x = 0$ となるため, $A$ は多重度1の固有値 $n - 1$ と多重度 $n - 1$ の固有値 $- 1$ を持ちます. このことから $P$ の固有値は $1$ と $- 1 / (n - 1)$ です.

3. エクスパンダー

エクスパンダーグラフの定義は色んな仕方があります. この記事では以下で定めた $λ$ -エクスパンダーという概念を考えます (他にも定義4の $(n, d, λ)$ -エクスパンダーという用語も知られていますがこの定義は本記事ではここ以外では取り上げないので, 本記事を読む上では覚えなくても構いません).

λ

-エクスパンダー

グラフ $G$ の遷移確率行列の固有値を大きい順に $1 = λ_{1} \geq \dots λ_{n} \geq - 1$ とする. $max {| λ_{2} |, | λ_{n} |} \leq λ$ を満たすとき, $G$ を $λ$ -エクスパンダー(expander)と呼ぶ.

(n, d, λ)

-エクスパンダー

$n$ 頂点 $d$ -正則グラフ $G$ が $λ$ -エクスパンダーであるとき, $G$ を特に $(n, d, λ)$ -エクスパンダーと呼ぶ.

簡潔に言えば, 非自明な固有値 $max {| λ_{2} |, | λ_{n} |}$ が全て小さい値をとるときにそのグラフをエクスパンダーといいます. 任意のグラフは $1$ -エクスパンダーですが, 特に二部グラフは明らかに $1$ -エクスパンダーです. 命題3で主張したように二部グラフは固有値に対称性があるので $λ_{n} = - λ_{1}$ も自明な固有値に含まれてしまいます. 二部グラフに対してエクスパンダーを議論したい場合は $max {| λ_{2} |, | λ_{n - 1} |} = | λ_{2} |$ を考えることがあります. 本記事では特にこのようなことはせず, 二部グラフは1-エクスパンダーであるとします(なので二部グラフに対しては自明な事実しか言えません).

専門家向けの注釈(断り):
正則グラフに対してエクスパンダーなものを定義して議論するという文献が非常に多いため, 定義4の方が知れ渡っています. しかしそうすると正則でないグラフに対する議論などができないので本記事では定義3を採用しています. また, グラフラプラシアン $L$ を使ったエクスパンダーの定義もよく知られています. しかし, 遷移確率行列の固有値を考えた方がExpander Mixing Lemmaの導入が楽なので遷移確率行列による定義を採用しました.)

エクスパンダーグラフは線形代数のテクニックと非常に親和性が高く, 面白い性質が多く知られています. 以降では, $λ$ -エクスパンダーの色んな性質を紹介していきます. 結論から言えばエクスパンダーは辺が $(\binom{V}{2})$ の全体に満遍なく散らばっているという構造的性質を持つことを見ていきます.

4. Expander Mixing Lemma

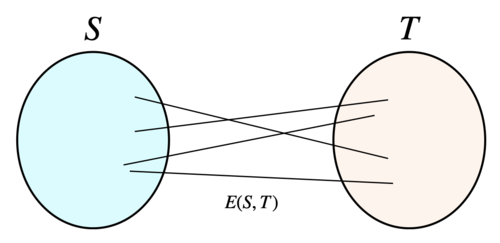
$G = (V, E)$ を正則グラフとします. 二つの頂点部分集合 $S, T \subseteq V$ に対して $E (S, T) = {(u, v) \in E : u \in S, v \in T}$ とします. 言い換えれば, $E (S, T)$ は $S$ と $T$ の間にある辺の集合になっていて, $| E (S, T) |$ が大きいほど $S T$ 間の結合が強いことを意味します.

E(S,T)1 E(S,T)1

特に, $S \cap T \neq \emptyset$ のとき, $| E (S, T) |$ は $S \cap T$ 内の辺を2回カウントすることに注意してください. 例えば下図では辺 ${u, v}$ が $S \cap T$ に含まれているため, $E (S, T) = {(u, v), (v, u)}$ なので $| E (S, T) | = 2$ です.

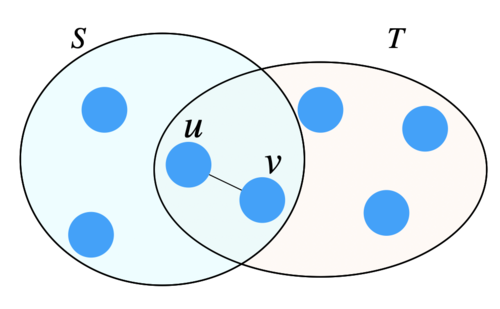E(S,T)2 E(S,T)2

正則グラフに対するExpander Mixing Lemma

$G = (V, E)$ を $d$ -正則かつ $λ$ -エクスパンダーとする. このとき, 任意の $S, T \subseteq V$ に対して
$\begin{array}{r} | | E (S, T) | - \frac{d | S | | T |}{n} | \leq d λ \sqrt{| S | | T |} . \end{array}$

定理4の気持ちを述べます. グラフ $G$ は $d$ -正則グラフなので, $| E | = \frac{n d}{2}$ です. グラフは最大で $(\binom{n}{2})$ 本の辺を持ちうるので, $G$ の辺密度は $| E | / (\binom{n}{2}) \approx \frac{d}{n}$ になります. Expander Mixing Lemmaは, 小さい $λ$ に対してグラフが $λ$ -エクスパンダーであるならば, この辺は $(\binom{V}{2})$ に満遍なく散らばっているということを主張している定理です. 満遍なく辺が散らばっているとき, どの二つの頂点集合 $S, T \subseteq V$ に対して $S T$ 間の辺の密度は全体の辺密度 $d / n$ とほぼ同じ値になります. すなわち, $| E (S, T) | \approx \frac{d}{n} | S | | T |$ となります. Expander Mixing Lemmaはこの $\approx$ の評価を行っていると解釈することができます.

(注: この証明で出てくる行列のノルムや付随する不等式については本記事の最後の章に付録として定義などを載せてあるので, 分からない方はそれを参照してください)

頂点部分集合 $U \subseteq V$ に対し, $1_{S} \in {0, 1}^{V}$ を $U$ の指示ベクトルとする. すなわち
$\begin{array}{r} (1_{S})_{u} = {\begin{cases} 1 & if u \in U, \\ 0 & otherwise . \end{cases} \end{array}$
$A$ を $G$ の隣接行列とし, 行列 $A - \frac{d}{n} 1 1^{⊤}$ について
$\begin{array}{r} 1_{S}^{⊤} (A - \frac{d}{n} 1 1^{⊤}) 1_{T} = \sum_{u, v \in V} A_{u, v} (1_{S})_{u} (1_{T})_{v} - \frac{d}{n} | S | | T | = | E (S, T) | - \frac{d}{n} | S | | T | \end{array}$
となります. 一方で, Cauchy-Schwarzの不等式より
$\begin{aligned} | 1_{S}^{⊤} (A - \frac{d}{n} 1 1^{⊤}) 1_{T} | & \leq ∥ 1_{S} ∥ ∥ 1_{T} ∥ ‖ A - \frac{d}{n} 1 1^{⊤} ‖ \\ \leq \sqrt{| S | | T |} sup_{x \neq 0} | R (x; A - \frac{d}{n} 1 1^{⊤}) | \end{aligned}$
ここで, $∥ M ∥$ は行列 $M$ のスペクトルノルム, $R (x; M) = \frac{x^{⊤} M x}{x ⊤ x}$ は行列 $M$ のレイリー商としています (付録A参照).

行列 $M = A - \frac{d}{n} 1 1^{⊤}$ とおき, そのレイリー商 $R (x; M)$ を評価します. $G$ が $d$ 正則なので, $A 1 = d 1$ . すなわち $M 1 = 0$ となるので, $x = α 1 + β v \neq 0$ とすると(ここで $v$ は $1$ と直交),
$\begin{array}{r} x^{⊤} M x = β x^{⊤} M v = β (M x)^{⊤} v = β^{2} v^{⊤} M v . \end{array}$
今, $| R (x; M) |$ を最大化する $x$ を考えると, $∥ x ∥^{2} = α^{2} n + β^{2} ∥ v ∥^{2}$ より, $α = 0$ でなければなりません. このとき $R (x; M) = \frac{v^{⊤} M v}{v^{⊤} v}$ となりますが, $v$ の直交性から $1 1^{⊤} v = 0$ なので, $M v = A v$ となることから, $R (x; M) = R (x; A)$ です. $v$ は $A$ の第一固有ベクトル $1$ に直交しているので, $sup_{v \neq 0 : v ⊥ 1} | R (v; A) | = max {| λ_{2} (A), λ_{n} (A)}$ です ( $λ_{i} (A)$ は行列 $A$ の $i$ 番目に大きい固有値). 仮定よりグラフ $G$ は $λ$ -エクスパンダーなので, $max {| λ_{2} (A), λ_{n} (A)} \leq d λ$ です. 今までの議論をまとめると
$\begin{aligned} | | E (S, T) | - \frac{d}{n} | S | | T | | & = | 1_{S}^{⊤} (A - \frac{d}{n} 1 1^{⊤}) 1_{T} | \\ \leq \sqrt{| S | | T |} sup_{x \neq 0} | R (x; A - \frac{d}{n} 1 1^{⊤}) | \\ \leq d λ \sqrt{| S | | T |} \end{aligned}$
を得ます.

一般グラフに対するExpander Mixing Lemma

非正則グラフに対するExpander Mixing Lemmaはあまりグラフ理論の文脈では注目されていませんが, ランダムウォークの理論では知れ渡っています. 定理の主張を述べるために少し準備します.

定常分布

グラフ $G = (V, E)$ に対してベクトル $π = {(\frac{\deg (v)}{2 | E |})}_{v \in V} \in [0, 1]^{V}$ を定常分布(stationary distribution)という.

実際, 定常分布 $π$ は $V$ 上の確率分布になります. というのも握手補題より, $\sum_{v \in V} \deg (v) = 2 | E |$ なので, $\sum_{v \in V} π_{v} = 1$ になります. 例えば $G$ が正則グラフの場合は $π$ は $V$ 上の一様分布になります. また, $π$ は $P$ の左固有ベクトルになっていて, $π P = π$ を満たすことが簡単に確認できます. このことから, 適当な初期分布 $μ \in [0, 1]^{V}$ から始めて $μ_{i + 1} = μ P$ と定義すると, 適当の条件下で $μ_{t}$ は $π$ に収束することが示せます. これが「定常」分布たる所以です.

最後に以下を定義します:

$S \subseteq V$ に対し, $π_{S} = \sum_{v \in S} π_{v}$ .
$v \in V$ と $S \subseteq V$ に対し, $P_{v, S} = \sum_{w \in S} P_{v, w}$ .
$S, T \subseteq V$ に対し, $Q (S, T) = \sum_{v \in S} π_{v} P_{v, T}$ .

$Q (S, T)$ はマルコフ連鎖理論においてedge measure[2]と呼ばれる値で, 実は $Q (S, T) = Q (T, S)$ が成り立ちます. また, $P_{v, S}$ は「 $v$ の隣接点をランダムに選んだときにその点が $S$ に含まれている確率」と解釈することができます. 例えば $G$ が $d$ -正則のときは $π_{v} = \frac{1}{n}$ , $P_{v, S} = \frac{| E ({v}, S) |}{d}$ より
$\begin{array}{r} Q (S, T) = \frac{1}{n d} \sum_{v \in S} | E ({v}, T) | = \frac{| E (S, T) |}{n d} \end{array}$
となります.

一般グラフのExpander Mixing Lemma

グラフ $G = (V, E)$ が $λ$ -エクスパンダーならば, 任意の $S, T \subseteq V$ に対し
$\begin{array}{r} | Q (S, T) - π_{S} π_{T} | \leq λ \sqrt{π_{S} π_{T}} . \end{array}$

定理5の証明は本記事では省きますが, 文献[2]に載っています. また, $G$ が正則グラフの場合, 定理5は定理4と等価になります.

5. Cheegerの不等式

Cheeger定数やCheegerの不等式は多様体の文脈で知られている結果ですが, その離散の世界における解釈がグラフ理論で知られています. 導入を単純にするために, まずは正則グラフを考え, そのあとに一般のグラフに対するCheegerの不等式を紹介します.

正則グラフの辺拡張率

$d$ -正則グラフ $G = (V, E)$ とその頂点部分集合 $S \subseteq V$ に対し, 辺拡張率(edge expansion) $ϕ (S)$ を $ϕ (S) = \frac{| E (S, V ∖ S) |}{d | S |}$ で定める. グラフ $G$ の辺拡張率(またはCheeger定数) $ϕ (G)$ を $ϕ (G) = min_{0 \leq | S | \leq n / 2} ϕ (S)$ で定める.

頂点部分集合 $S \subseteq V$ に対して $d | S | = \sum_{v \in S} \deg (v)$ は $S$ に接続している辺の総数になっていて, $| E (S, V ∖ S) |$ はこれらの辺のうち $S$ の外側と繋がっているものをカウントしています. つまり, $ϕ (S)$ が大きいということは $S$ の辺のうち外部 $V ∖ S$ に接続しているものが多いということを意味しており, $ϕ (S)$ が小さいということは $S$ は外部から孤立気味になっているということを意味します.

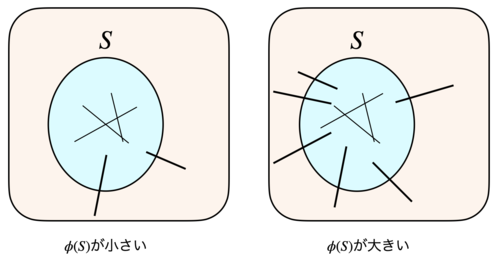phi phi

Cheegerの不等式

正則グラフ $G$ の正則化されたグラフラプラシアン $\tilde{L}$ の第二固有値(i.e., 二番目に大きい固有値)を $λ_{2}$ とする. このとき
$\begin{array}{r} \frac{λ_{2}}{2} \leq ϕ (G) \leq \sqrt{2 λ_{2}} . \end{array}$

$d$ -正則グラフの $\tilde{L}$ は $\tilde{L} = I - P$ となるので, $1 = μ_{1} \geq \dots \geq μ_{n}$ を $P$ の固有値とすると, $1 - μ_{i} = λ_{i}$ となります. したがってCheegerの不等式は遷移確率行列の言葉を使うと次のように言い直すことができます.

正則グラフ $G$ の遷移確率行列 $P$ の固有値を $1 = μ_{1} \geq \dots \geq μ_{n} \geq - 1$ とする. このとき,
$\begin{array}{r} \frac{1 - μ_{2}}{2} \leq ϕ (G) \leq \sqrt{2 (1 - μ_{2})} . \end{array}$

特に $G$ がエクスパンダーのとき, $| μ_{2} |$ が小さいので $ϕ (G)$ が大きいはずです. すなわちどの $S \subseteq V$ に対して $ϕ (S)$ が大きいので, どの $S$ に対しても $S$ は孤立気味になっていないということになり, 結果としてExpander Mixing Lemmaの帰結(辺が満遍なく分散している)のようなことがわかります.

一般グラフに対するCheegerの不等式

5章で定義したedge measure $Q (S, T)$ と定常分布 $π$ を思い出してください. 特に, $π_{S} = \sum_{v \in V} π_{v}$ です. $G$ が正則グラフの場合は $Q (S, T) = \frac{| E (S, T) |}{n d}$ 及び $π_{S} = \frac{d | S |}{n}$ となります.

一般グラフの辺拡張率

グラフ $G = (V, E)$ とその頂点部分集合 $S \subseteq V$ に対し, 辺拡張率 $ϕ (S)$ を $ϕ (S) = \frac{Q (S, V ∖ S)}{π_{S}}$ で定める. また, グラフ $G$ の辺拡張率 $ϕ (G)$ を $ϕ (G) = min_{0 < π_{S} \leq 1 / 2} ϕ (S)$ で定める.

特に, 命題1の証明より, $\tilde{L}$ の固有値 $λ_{i}$ と $P$ の固有値 $μ_{i}$ の間には $μ_{i} = 1 - λ_{i}$ という関係が成り立つので, 定理7は遷移確率行列の言葉で言い直すこともできます.

一般グラフに対するCheegerの不等式

グラフ $G$ の正規化したグラフラプラシアン $\tilde{L}$ の第二固有値を $λ_{2}$ とする. このとき,
$\begin{array}{r} \frac{λ_{2}}{2} \leq ϕ (G) \leq \sqrt{2 λ_{2}} \end{array}$

7. 結論

グラフ理論でよく見かけるエクスパンダーというグラフの性質を見てきました. 特に, グラフの構造的性質をそれに付随する行列の固有値から導出していくスペクトルグラフ理論という理論の紹介を簡単に行い, その後にExpander Mixing LemmaとCheegerの不等式を紹介しました. 正則グラフに対するExpander Mixing Lemma(定理4)の証明を見ると分かるように, 線形代数の色んな道具を使っています. グラフという組合せ論的なものの性質を線形代数を使って解析できるというのが面白いですね.

8. Notes

参考文献[1]はマルコフ連鎖の非常に有名な英語書籍で, ランダムウォークなどを学びたい方にはおすすめです. 色んな結果が載っているので論文を書くときに引用されることも多いです.
参考文献[2]は計算量理論の非常に有名な本です. 英語で書かれていますが, 幅広いトピックを網羅しており, 21章と22章ではエクスパンダーグラフを応用した様々な理論的結果を紹介しています.

付録A. 線形代数の復習 (ノルム)

行列やベクトルのノルムとその基本的な性質を書いておきます. 知っている方は読まなくても大丈夫です. この記事では基本的に実ベクトルや実行列を扱います.

ユークリッドノルム, スペクトルノルム

ベクトル $x = (x_{1}, \dots, x_{n}) \in R^{n}$ に対し, そのユークリッドノルム(Euclidean norm) $∥ x ∥$ を $∥ x ∥ = {(\sum_{i = 1}^{n} x_{i}^{2})}^{1 / 2}$ で定める.

行列 $M \in R^{n \times n}$ に対し, そのスペクトルノルム(spectral norm) $∥ M ∥$ を $∥ M ∥ = sup_{x \neq 0} \frac{∥ M x ∥}{∥ x ∥}$ で定める.

次の命題は $∥ M ∥$ の定義より明らかですが, よく使います.

任意のベクトル $x \in R^{n}$ と行列 $M \in R^{n \times n}$ に対し, $∥ M x ∥ \leq ∥ M ∥ ∥ x ∥$ .

Cauchy-Schwarzの不等式

任意のベクトル $x, y \in R^{n}$ に対して, $x^{⊤} y \leq ∥ x ∥ ∥ y ∥$ .

スペクトルノルムと特異値・固有値の関係

任意の行列 $M$ に対し, $∥ M ∥$ は $M^{⊤} M$ の最大固有値の平方根に等しい. 特に, $M$ が対称行列のときは $∥ M ∥ = max_{i = 1, \dots, n} | λ_{i} |$ . ただし $λ_{1}, \dots, λ_{n}$ は $M$ の固有値.