文献あり

自作問題の解答: 外心と垂心を焦点とする内接楕円

問題: 019

鋭角三角形$\mr{ABC}$について、その外心を$\mr{O}$、垂心を$\mr{H}$とする。2点$\mr{O,H}$を焦点に持ち、$\triangle\mr{ABC}$に内接する楕円の面積は$\triangle\mr{ABC}$の面積の何倍か。角$\angle A,\angle B,\angle C$を用いて表せ。またどのような三角形のときに最大となるか示し、その最大値を求めよ。
なお、$\mr{H}$と$\mr{O}$が一致する場合には内接円をこの楕円とみなす。

Twitterに投稿した自作問題です。

解説

各頂点から対辺に下した垂線の足を$\mr{H_A,H_B,H_C}$、各辺$\mr{BC,CA,AB}$の中点をそれぞれ$\mr{M_A,M_B,M_C}$とする。辺の長さについて$\mr{BC}=a$, $\mr{CA}=b$, $\mr{AB}=c$、外接円の半径を$R$とする。楕円と各辺$\mr{BC,CA,AB}$との接点をそれぞれ$\mr{T_A,T_B,T_C}$とし、長軸半径を$d$、短軸半径を$e$、中心と焦点の距離を$f$とする。

楕円の性質として、$\mr{OT_A}+\mr{HT_A}=2d$であり、$\angle\mr{M_AT_A}=\angle\mr{H_AT_AH}$である。このことから、辺$\mr{BC}$について点$\mr{O}$と対称な点$\mr{O'}$を取ると、3点$\mr{H,T_A,O'}$は1直線上に並び、$\mr{HO'}=2d$となる。

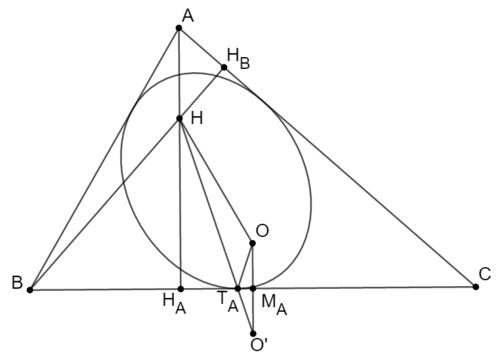Fig.019_1

$\mr{BM_A}=\mr{CM_A}=\dfrac{a}{2}$, $\mr{BH_A}=c\cos B$, $\mr{CH_A}=b\cos C$, $a=b\cos C+c\cos B$より、$\mr{H_AM_A}=\dfrac{1}{2}|b\cos C-c\cos B|$である。また$\mr{OM_A}=R\cos A$。さらに$\angle\mr{BHH_A}=\angle C$より、$\mr{HH_A}=\dfrac{\mr{BH_A}}{\tan C}=\dfrac{c\cos B \cos C}{\sin C}=2R\cos B\cos C$。
以上のことから、$\mr{HO'}^2=\mr{H_AM_A}^2+(\mr{\mr{HH_A+OM_A}})^2=4d^2$であって、
\begin{aligned} 4d^2&=\frac{1}{4}(b\cos C-c\cos B)^2+(2R\cos B\cos C+R\cos A)^2 \\ &=\frac{1}{4}(b^2\cos^2C+c^2\cos^2B-2bc\cos B\cos C)+4R^2\cos^2B\cos^2C+R^2\cos^2A+4R^2\cos A\cos B\cos C \\ &=\frac{1}{4}(a^2-4bc\cos B\cos C)+4R^2\cos^2B\cos^2C+R^2\cos^2A+4R^2\cos A\cos B\cos C \\ &=R^2\sin^2 A-4R^2\sin B\sin C\cos B\cos C+4R^2\cos^2B\cos^2C+R^2\cos^2A+4R^2\cos A\cos B\cos C \\ &=R^2+4R^2\cos B\cos C(\cos B\cos C-\sin B\sin C)+4R^2\cos A\cos B\cos C \\ &=R^2+4R^2\cos B\cos C\cos(B+C)+4R^2\cos A\cos B\cos C \end{aligned}
となるが、$\cos(B+C)=\cos(\pi-A)=-\cos A$であるから、$4d^2=R^2$を得る。
続いて、$\mr{HO}^2=\mr{H_AM_A}^2+(\mr{HH_A-OM_A})^2=4f^2$であって、
\begin{aligned} 4f^2&=\frac{1}{4}(b\cos C-c\cos B)^2+(2R\cos B\cos C-R\cos A)^2 \\ &=\cdots \\ &=R^2-8R^2\cos A\cos B\cos C \end{aligned}
を得る。楕円として$d^2=e^2+f^2$だから、$e^2=2R^2\cos A\cos B\cos C$である。したがって、$d=\dfrac{R}{2}$, $e=R\sqrt{2\cos A\cos B\cos C}$となり、楕円の面積は$\pi de$で求められる。
$$ \pi de=\frac{\pi R^2}{\sqrt{2}}\sqrt{\cos A\cos B\cos C} $$

$\mr{H}$と$\mr{O}$が一致するのは明らかに正三角形のときである。$\cos A=\cos B=\cos C=\dfrac{1}{2}$を代入すると
$$ \pi de=\frac{\pi R^2}{\sqrt{2}}\cdot\frac{1}{2\sqrt{2}}=\pi \left(\frac{R}{2}\right)^2 $$
となるが、正三角形において内接円半径は外接円半径の$\dfrac{1}{2}$倍だからこれは内接円の面積に等しい。よって$\mr{H}$と$\mr{O}$が一致するときもよい。

$\triangle\mr{ABC}$の面積$S$について、
$$ S=\frac{1}{2}bc\sin A=2R^2\sin A\sin B\sin C $$
と書けるから、求めるものは
$$ \dfrac{\pi de}{S}=\frac{\pi \sqrt{\cos A\cos B\cos C}}{2\sqrt{2}\sin A\sin B\sin C} $$

$\triangle\mr{ABC}$は鋭角三角形であり、$\sin A$,$\cos A$などはすべて正だから、$\dfrac{\pi de}{S}$が最大となるのは、
$$ \frac{\cos A\cos B\cos C}{\sin^2 A\sin^2 B\sin^2 C}=\frac{\cos A}{1-\cos^2 A}\cdot\frac{\cos B}{1-\cos^2 B}\cdot\frac{\cos C}{1-\cos^2 C} $$
が最大となるときである。余弦定理を用いて辺の長さで表し、さらに$a=y+z$, $b=z+x$, $c=x+y$と変換すると、
$$ \frac{\cos A}{1-\cos^2 A}=\frac{x^2(x+y+z)^2-y^2z^2}{4xyz(x+y+z)} $$
となる。これは$x,y,z$をすべて定数倍しても値が変わらないから、$x+y+z=1$としてよい。するとこれは$\dfrac{\cos A}{1-\cos^2 A}=\dfrac{1}{4}\left(\dfrac{x}{yz}-\dfrac{yz}{x}\right)$ となる。$\angle\mr{B,C}$についても同様に、$\dfrac{\cos B}{1-\cos^2 B}=\left(\dfrac{y}{zx}-\dfrac{zx}{y}\right)$, $\dfrac{\cos C}{1-\cos^2 C}=\dfrac{1}{4}\left(\dfrac{z}{xy}-\dfrac{xy}{z}\right)$。

鋭角三角形の成立条件から$b+c-a=2x>0$, $b^2+c^2-a^2=2x(x+y+z)-2yz=2x-2yz>0$を得る。さらに対称性から、$x>yz>0$, $y>zx>0$, $z>xy>0$が従う。

$\dfrac{yz}{x}=\alpha^2$, $\dfrac{zx}{y}=\beta^2$, $\dfrac{xy}{z}=\gamma^2$とおくと、
$$ \frac{\cos A}{1-\cos^2 A}\cdot\frac{\cos B}{1-\cos^2 B}\cdot\frac{\cos C}{1-\cos^2 C}=\frac{1}{4^3}\cdot\left(\dfrac{1}{\alpha^2}-\alpha^2\right)\left(\dfrac{1}{\beta^2}-\beta^2\right)\left(\dfrac{1}{\gamma^2}-\gamma^2\right) $$
となる。ここで$0<\alpha^2,\beta^2,\gamma^2<1$であり、$\alpha^2\beta^2=z^2$,$\beta^2\gamma^2=x^2$,$\gamma^2\alpha^2=y^2$である。$\alpha,\beta,\gamma$は正の値を考えれば十分だから、$x+y+z=1$より$\alpha\beta+\beta\gamma+\gamma\alpha=1$が従う。$\alpha+\beta+\gamma=p$,$\alpha\beta\gamma=q$とすると次を得る。
\begin{aligned} &\frac{1}{4^3}\cdot\left(\dfrac{1}{\alpha^2}-\alpha^2\right)\left(\dfrac{1}{\beta^2}-\beta^2\right)\left(\dfrac{1}{\gamma^2}-\gamma^2\right) \\ =&\frac{1}{4^3\alpha^2\beta^2\gamma^2}(1-\alpha^4)(1-\beta^4)(1-\gamma^4) \\ =&\frac{1}{4^3\alpha^2\beta^2\gamma^2}(1-(\alpha^4+\beta^4+\gamma^4)+(\alpha^4\beta^4+\beta^4\gamma^4+\gamma^4\alpha^4)-\alpha^4\beta^4\gamma^4) \\ =&\frac{4(p-q)^2-(p^2-q^2)^2}{4^3q^2} \end{aligned}

関数$f(t)=t^3-pt^2+t-q$をおくとき、3次方程式$f(t)=0$が$0<\alpha,\beta,\gamma<1$なる3実数解を持つための$p,q$の条件は、(i): $f'(t)=0$が実数解$u,v$ (ただし$0< u\le v<1$) を持ち、(ii): $f(u)\cdot f(v)\le 0$であり、(iii): $f(0)<0$かつ$f(1)>0$であること。

(i)について、$f'(t)=3t^2-2pt+1$より、$\dfrac{D}{4}=p^2-3\ge 0$かつ、軸について$0<\dfrac{p}{3}<1$かつ、$f'(0)=1>0$かつ、$f'(1)=4-2p>0$であればよいので、$\sqrt{3}\le p<2$。

(ii)について、$f'(t)=0$における解と係数の関係によって$u+v=\dfrac{2}{3}p$, $uv=\dfrac{1}{3}$であることを踏まえて、
\begin{aligned} f(u)\cdot f(v)&=(u^3-pu^2+u-q)(v^3-pv^2+v-q) \\ &=\cdots = \frac{4}{27}p^3q-\frac{1}{27}p^2-\frac{2}{3}pq+q^2+\frac{4}{27} \le 0 \end{aligned}
ここで$p$を固定して$q$についての2次不等式とみると、次のように解ける。なお、(i)より$x^2-3\ge 0$である。
$$ -\frac{2}{27}p^3+\frac{1}{3}p-\frac{2}{27}\sqrt{(p^2-3)^3} \le q\le -\frac{2}{27}p^3+\frac{1}{3}p+\frac{2}{27}\sqrt{(p^2-3)^3} $$

(iii)について、$f(0)=-q<0$かつ$f(1)=2-p-q>0$であるから、$0< q<2-p$。

(i),(ii),(iii)の下での
$$ \frac{4(p-q)^2-(p^2-q^2)^2}{4^3q^2}=\frac{(p-q)^2(4-(p+q)^2)}{4^3q^2} \quad\cdots(\text{＊}) $$
の最大値を求めればよい。
$$ \frac{d}{dp}\left(-\frac{2}{27}p^3+\frac{1}{3}p\pm\frac{2}{27}\sqrt{(p^2-3)^3}\right)=-\frac{2}{9}p\left(p\pm\sqrt{p^2-3}\right)+\frac{1}{3} $$
であり、常に$p\left(p\pm\sqrt{p^2-3}\right)>\dfrac{3}{2}$だからこれは負となる。したがって、
$$ 0< -\frac{2}{27}p^3+\frac{1}{3}p\pm\frac{2}{27}\sqrt{(p^2-3)^3} \le \frac{1}{3\sqrt{3}} $$
が従う。このことから(i)の範囲では$-p< q< p$であることがわかるので、(＊)は、$p$を固定した時$q$が小さいほど大きな値をとり、$q$を固定した時$p$が小さいほど大きな値をとることがわかる。(i)より$p=\sqrt{3}$とすると、(ii)より$q=\dfrac{1}{3\sqrt{3}}$となるから、このときに(＊)は最大値$\dfrac{8}{27}$をとる。

さてこのとき$f(t)=t^3-\sqrt{3}t^2+t-\dfrac{1}{3\sqrt{3}}=\left(t-\frac{1}{\sqrt{3}}\right)^3$となるから、$\alpha=\beta=\gamma=\dfrac{1}{\sqrt{3}}$で、$x=y=z=\dfrac{1}{3}$を得て、$a=b=c$が従うから、$\triangle\mr{ABC}$は正三角形である。

以上のことから、題意の楕円の面積は$\triangle\mr{ABC}$の面積の$\dfrac{\pi \sqrt{\cos A\cos B\cos C}}{2\sqrt{2}\sin A\sin B\sin C}$倍であり、この値は$\triangle\mr{ABC}$が正三角形のときに最大値$\dfrac{\pi}{3\sqrt{3}}$を取る。

ネタバレ含むコメント

三角形の内接あるいは傍接楕円の2つの焦点は互いに等角共役となります(文献参照のこと)。このことと、外心と垂心が互いに等角共役であることからこの問題を作成しました。面積比についてはすんなりと求まりましたが、最大値はかなり苦労しました。きれいに解く方法をご存じの方がいらっしゃいましたらコメント頂けると幸いです。