曲面の交点としての線形相補性問題

はじめに

本記事では，数理計画問題の一つである線形相補性問題(linear complementarity problem; LCP)[1]を紹介します．

ご存じの方にとっては，LCPは最適化問題や双行列ゲームなどを包含する広い問題クラスであり，それらを統一的に議論するための「枠組み」であるという印象が強いかと思います．一方で，LCP自身に興味を持っている方は少ないのではないでしょうか？

本記事では，LCP自身のおもしろさを知っていただくために，その幾何的な解釈を紹介します．結論として，LCPは「複数の曲面の交点を求める問題」であり，非常に基礎的であると言えます．そして，その特殊ケースでは，解を簡単に計算できると予想されていながら，その結論は未解決問題となっています．（本記事では「簡単に解ける」を「大規模な問題でも高速に解ける」という意味で使います．）

このように，LCPはさまざまな問題を統一的に議論するための枠組みであるのに加え，問題自身にも興味深い話題がたくさんあります．この機会に，LCP自身に興味を持っていただければと思います．

以下では，平面の交点を求める問題から導入し，それを曲面の交点を求める問題に拡張します．そして，曲面の交点を求める問題がLCPと一致することを紹介します．

平面の交点

まずは，複数の平面の交点を求めてみましょう．一般には，$n$次元空間上の$n$枚の超平面（超曲面）の交点を求めます．例えば，2次元空間上の2本の直線（曲線），3次元空間上の3枚の平面（曲面），...，となります．簡単のため，本記事では，2次元空間上の2本の直線（曲線）の交点を求めます．

直線は線形方程式（$a_1 x_1 + a_2 x_2 + b = 0$の形式）の解の集合として表せます．したがって，直線の交点は，2つの線形方程式（線形方程式系）を同時に満たす解となります．

例えば，以下の図では，2本の直線はそれぞれ$2 x_1 - x_2 - 2 = 0, x_1 - 2 x_2 + 2 = 0$と表せます．この線形方程式系を解くと，交点は$(2, 2)$となります．

図１

$n = 2, 3$の場合，中学校で習ったように，線形方程式系は式の足し引きで簡単に解けます．一般の$n$についても，一定の規則にしたがって式を足し引きしていくことで，解を簡単に計算できることが知られています．例えば，ガウスの消去法がメジャーな方法です[2]．

曲面の交点

次に，複数の曲面の交点を求めてみましょう．例えば，以下の図のように，2本の曲線を考えてみます．当然，直線に比べて曲線はさまざまな形があります．さらに，解が複数ある場合もあり得ます．一般に，複数の曲面の交点を求めるのは簡単ではありません．

図２

凸曲面の交点

一般の凸曲面の交点を求めるのは難しいので，簡単に解を計算できそうなケースを考えてみましょう．例えば，曲線がグネグネしていないケースを仮定してみます．具体的には，曲面が凸多面体の境界面（凸曲面）で定義されているとします．曲面は非有界であっても大丈夫です．

例えば，以下の図では，曲線C1は多面体P1，曲線C2は多面体P2の境界面で定義されています．カクカクしているので表現できる曲線が少ないように感じますが，多面体を構成する面の数を増やせばなめらかにできます．

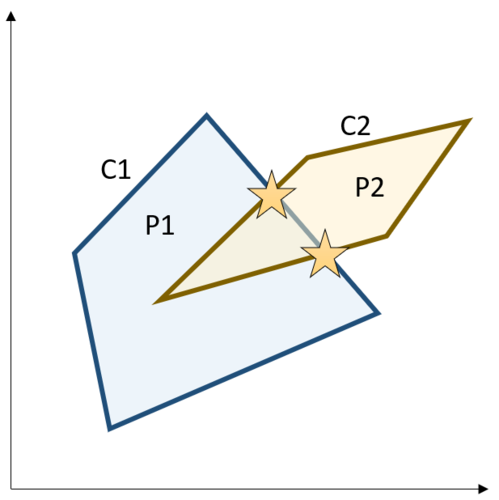図３

そして，今回の主役であるLCPは，凸曲面の交点を求める問題と一致します．では，LCPを形式的に定義します．$n$次元空間上に$n$枚の凸曲面があるとします．凸曲面を定義する凸多面体は複数個の半空間の交差として表せます．$i$番目の凸多面体が$m_i$個の半空間で構成されるとします．また，その$j$番目の半空間がベクトル$a_{ij} \in \mathbb{R}^n$とスカラ$b_{ij} \in \mathbb{R}$を用いて$y_{ij} = a_{ij}^\top x + b \geq 0$と表されるとします．多面体の境界上の点は，少なくとも1つの半空間の境界上にあるので，$\prod_j y_{ij} = 0$が成り立ちます．この条件は「$y_{ij}$が互いに補いながら$= 0$を成り立たせる」ことから相補性条件と呼ばれます．これが相補性問題の名前の由来となります．以上より，LCPは多面体内かつ相補性条件を満たす点を求める問題となります．

\begin{align} \begin{matrix} \text{find} & & x \\ \text{subject to} & \forall i, j & y_{ij} = a_{ij}^\top x + b_{ij} \geq 0 \\ & \forall i & \prod_i y_{ij} = 0 \end{matrix} \end{align}

例えば，以下の図では，多面体P1は半空間$y_{11} = x_1 + 0 x_2 - 1 \geq 0, y_{12} = 0 x_1 + x_2 - 1 \geq 0$，多面体P2は半空間$y_{21} = - x_1 + 0 x_2 + 2 \geq 0, y_{22} = 0 x_1 - x_2 + 2 \geq 0$で構成されます．そして，相補性条件は$(x_1 + 0 x_2 - 1) (0 x_1 + x_2 - 1) = 0, (- x_2 + 0 x_2 + 2) (0 x_1 - x_2 + 2) = 0$となります．解は$(1, 2), (2, 1)$の2つとなります．

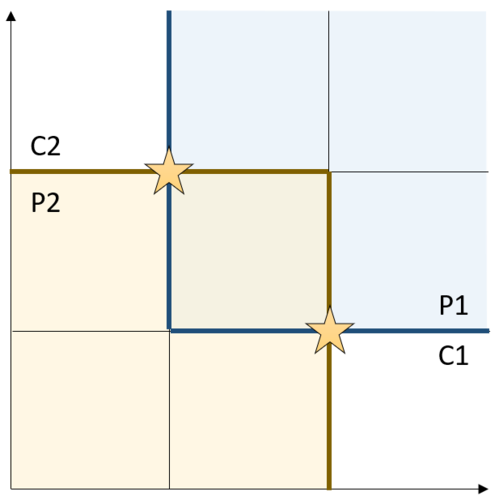図４

なお，本記事でのLCPの定義は，一般的な定義[1]とは異なっているので注意してください．本記事の方が広い定義となっています．

線形方程式系と同様に，LCPの解は簡単に計算できるのでしょうか？残念ながら，一般のLCPは簡単には解けないと考えられています[3]．

唯一解を持つ曲面の交点

簡単に計算できるように，さらにケースを絞ってみましょう．例えば，LCPは複数の解が存在しうるから難しい，と考えることができます．線形方程式系のように，解が1つしかない場合には簡単かもしれません．

しかし，線形方程式系とは異なり，曲面の位置が変わると交点の個数は変化する場合があります．例えば，以下の図左では交点が2つであるのに対して，図右では曲面を移動すると交点を4つにできます．そのため，LCPでは曲面が任意の位置で成り立つ性質に着目します．具体的には，曲線の位置を決めるのはスカラ$b_{ij}$なので，任意の$b_{ij}$で成り立つ性質です．

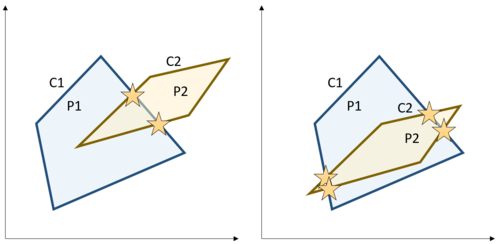図５

しかし，任意の$b_{ij}$で解が唯一となるケースはあるのでしょうか？ある$b_{ij}$では解が唯一であったとしても，別の$b_{ij}$では解が複数の場合があるので，自明ではありません．興味深いことに，そのようなケースが実際にあることが知られています．さらに，解が唯一となる必要十分条件までもが明らかになっています[4]．例えば，以下の図のようなケースです．曲面をいろいろ動かしてみて，解が必ず唯一になることを確かめてみてください．

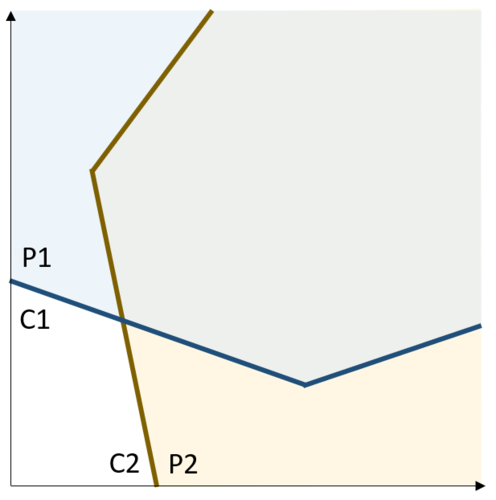図６

では，解が唯一の場合，曲面の交点は簡単に計算できるのでしょうか？この疑問は現時点では未解決問題となっています．ただし，簡単に解けるのではないかと予想されています[5]．なぜなら，この問題が簡単には解けないと仮定すると，計算複雑性理論におけるミレニアム問題であるP≠NP予想の結論がP=NPとなってしまうからです．逆に考えると，簡単に解けることが分かれば，P≠NPである可能性が残るわけです．簡単に解けようが解けまいが，この問題の解決は計算複雑性理論の進展に貢献することに違いはありません．

おわりに

本記事では，LCP自身のおもしろさを知っていただくために，その幾何的な解釈を紹介しました．私は中学校で連立方程式が直線の交点であることを知ったとき，数式が図の具体的な点として表されることに非常に感動したことを覚えています．そして，LCPでも同様の幾何的解釈ができることを知ったとき，再度震え上がりました．それ以来，LCPの幾何的な性質に惹かれています．ぜひ幾何的アプローチで未解決問題を解く糸口を見つけたいです．