最大公約数の和表示

和表示の意味って…

ここでは最大公約数を数列の総和にて表示する。ただしこの表示によって、計算量の減少や、なにかふかーい事実が得られるというわけではない。ただ、この和表示によってなにかしらの一つの新しい解釈が得られることは保証されよう(もしも既に知っていることだったら・・・う～ん残念！)。

道具

　ここでは級数表示のために使うあるアイディアを紹介する。おそらく多くの人が最大公約数と結びつけたことのない話題であろう。

直線と格子

格子点同士を結ぶ直線を考える(面倒くさいからExcelで撮影)。
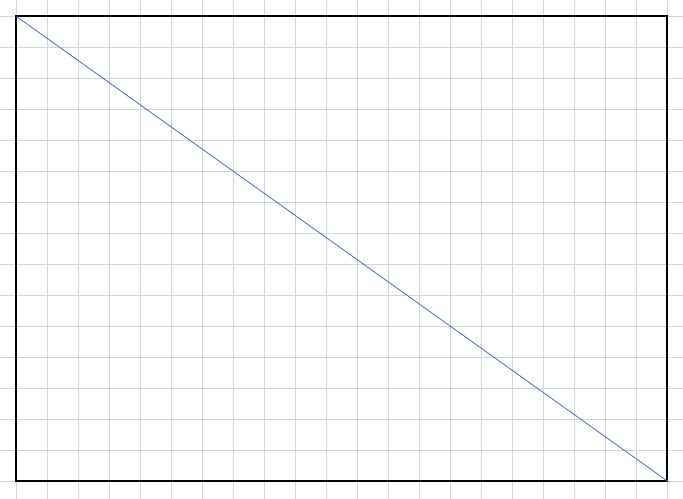Line
このときに、直線がいくつの正方形を通っているか、一度は考えたことがあるだろう。
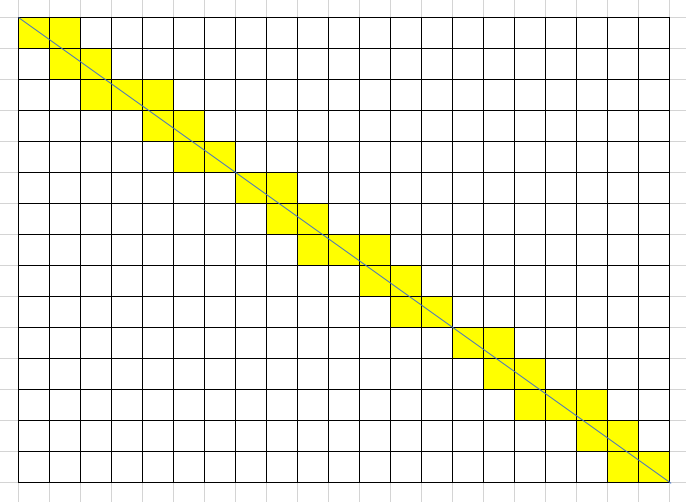LineBlock
これを具体的な式で表すことが今回の肝である。

通る正方形の個数

直線が通る正方形の数を考えるときに、直線がいくつの格子点を通るかが重要となる。$(x_1, y_1)$と$(x_2,y_2)$を結ぶ直線の通る(始点終点を除く)格子点の個数$n$は、明らかに次の式で与えられる。
$$ n=\gcd{(|x_1-x_2|,|y_1-y_2|)}-1 $$
ただし直線は垂直や水平でないものとする。
　ここで直線と、格子の線の交点に注目する
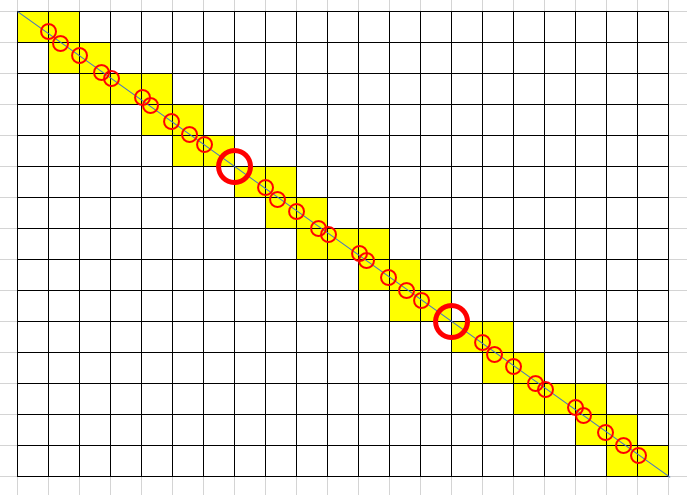LinePoints
小さい丸は格子の線と一回交わっている場所、大きな丸は格子点で交わっている場所を表している。
　左上から右下まで直線をゆっくりたどっていこう。

1. 左上の点から直線に沿って一つ目の正方形を進んでいくと、小さな赤い丸にたどり着く。そこで格子の線と交わっている。
2. 格子の線を越えてみよう。すると二つ目の正方形に入る。そのまま二つ目の正方形を進む。
3. 進んでいくとまた小さな赤い丸にたどり着く。そこでまた格子の線と交わっている。
4. また格子の線を越えてみよう。すると三つ目の正方形に入る。そのまま三つ目の正方形を進む。
5. これを繰り返していくと、大きな赤い丸にたどり着く。格子点だ。そこを超えると、また新しい正方形に入る。そこで進んでいくと、また小さい赤い丸にたどり着くはずだ。
6. 以下繰り返し・・・。

このように見てみると、あることが分かってくる。赤い丸である交点は、直線が通る隣り合う正方形と正方形の間に位置しているのだ。したがって、植木算より
「交点の個数$=$正方形の数 $-1$」
と分かる。じゃあ交点の個数は？これは直線の始点と終点の間にある、縦線と横線の個数に関係がある。小さい赤い丸の点では線と一回交わっている。一方で大きな赤い丸の点は格子点なので、縦線と横線両方に交わっている。だから
「交点の個数$=$縦線の数$+$横線の数$-$通る格子点の数」
となる。ここで$a=|x_1-x_2|,b=|y_1-y_2|$とすると、交点の個数は
$$ (a-1)+(b-1)-(\gcd{(a,b)}-1)=a+b-\gcd{(a,b)}-1. $$
となる。すると正方形の数は
$$ (a+b-\gcd{(a,b)}-1) + 1 = a+b-\gcd{(a,b)} $$
と表される。
図の例では$a=21, b=15$より、
$$ 21+15-\gcd{(21,15)}=21+15-3=33 $$
より、$33$つ通っているとわかる。
　ちなみにこの式を$\gcd{(a,b)}$で割るともう一つの導出方法も見えてくるが…これは各自に任せる。

和による正方形の個数表示

正方形の個数は求まった。でも考えてみてほしい。直線の通る正方形(図の黄色い部分)の個数を、一列ごとに足していけばいいのではないだろうか。
LineBlockSum
ここでやっと直線の式の出番だ。$(0,0)$と$(a,b)$を通る直線の方程式は$y=\frac{b}{a} x$であった。そして「一列ごとに足していく」には少々の工夫が必要である。次の図を見てもらいたい。
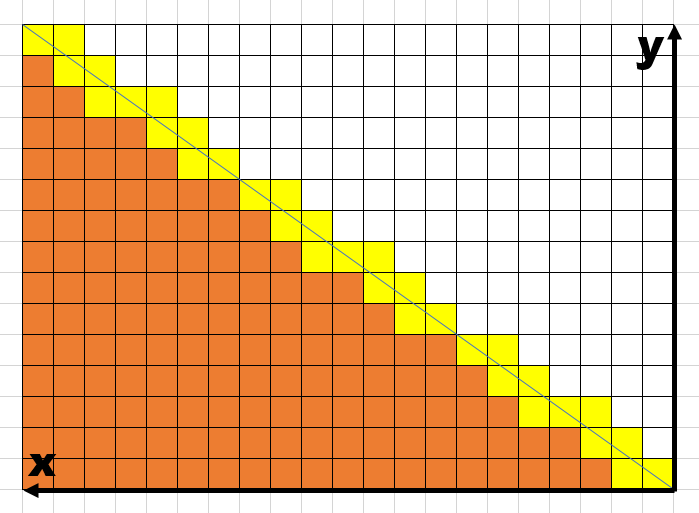LineBlockUnder
茶色のブロックは、$a\times b$の長方形内において、直線の下側にあるブロックである。この茶色ブロックの個数は、次の式で与えられる。
$$ \sum_{k=1}^{a-1} \left \lfloor \frac{bk}{a} \right \rfloor $$
そして直線の上側のブロック数も、下側のブロック数と同じである。よって、直線の通るブロック数は、
$$ ab-2\sum_{k=1}^{a-1} \left \lfloor \frac{bk}{a} \right \rfloor $$
である。ただし、$a=1$のときには総和部分を$0$とみなす。
　もしくは、黄色のブロックを直接求めることも可能だ。すなわち
$$ \sum_{k=0}^{a-1} \left( \left \lceil \frac{b(k+1)}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) $$

$2$つの数の最大公約数の和表示の導出

　道具の解説も終わったので、ついに和表示の導出である。とはいっても、直線の通る正方形の個数の表示式
$$ \begin{eqnarray} &&a+b-\gcd{(a,b)} \\ &&ab-2\sum_{k=1}^{a-1} \left \lfloor \frac{bk}{a} \right \rfloor \\ &&\sum_{k=0}^{a-1} \left( \left \lceil \frac{b(k+1)}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) \end{eqnarray} $$
を使うとばすぐ導出できる：
$$ \begin{eqnarray} \gcd{(a,b)} &=& a + b + 2 \sum_{k=1}^{a-1} \left \lfloor \frac{bk}{a} \right \rfloor -ab \\ &=& a + b - \sum_{k=0}^{a-1} \left( \left \lceil \frac{b(k+1)}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) \ \cdots (*) \end{eqnarray} $$
$(*)$を証明してみよう(これは正方形の個数の導出が帰納的で直感的、すなわち厳密性を欠いたものであったためだ)。まずは一行目の式を変形する：
$$ \begin{eqnarray} a + b + 2 \sum_{k=1}^{a-1} \left \lfloor \frac{bk}{a} \right \rfloor -ab &=& a + b + \sum_{k=1}^{a-1} \left( \left \lfloor \frac{bk}{a} \right \rfloor + \left \lfloor \frac{b(a-k)}{a} \right \rfloor \right) -ab \\ &=& a + b + \sum_{k=1}^{a-1} \left( \left \lfloor \frac{bk}{a} \right \rfloor + \left \lfloor \frac{-bk}{a} \right \rfloor +b \right) -ab \\ &=& a + b + \sum_{k=1}^{a-1} \left( \left \lfloor \frac{bk}{a} \right \rfloor - \left \lceil \frac{bk}{a} \right \rceil \right)+(a-1)b -ab \\ &=& a - \sum_{k=1}^{a-1} \left( \left \lceil \frac{bk}{a} \right \rceil - \left \lfloor \frac{bk}{a} \right \rfloor \right) \end{eqnarray} $$
これは$(*)$の二行目の式
$$ \begin{eqnarray} a + b - \sum_{k=0}^{a-1} \left( \left \lceil \frac{b(k+1)}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) &=& a + b - \left( \sum_{k=1}^{a-1} \left( \left \lceil \frac{bk}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) +b \right) \\ &=&a - \sum_{k=1}^{a-1} \left( \left \lceil \frac{bk}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) \end{eqnarray} $$
と一致している。また、この式に
$$ \begin{eqnarray} \left \lceil \frac{bk}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor = \left\{ \begin{array}{l} 1 \, (bk \equiv 0 \, ( \mathrm{mod}\, a)) \\ 0 \, (\mathrm{otherwise}) \end{array} \right. \end{eqnarray} $$
を適用することで
$$ \begin{eqnarray} a - \sum_{k=1}^{a-1} \left( \left \lceil \frac{bk}{a} \right \rceil -\left \lfloor \frac{bk}{a} \right \rfloor \right) &=& a- \{ ( a-1 ) - ( \gcd{(a,b)} - 1 ) \}\\ &=& \gcd{(a,b)} \end{eqnarray} $$
と証明ができる。

$3$つの最大公約数の和表示について

　先ほどの和表示は次の関係式を用いることで、一応拡張することができる
$$ \gcd{(a,b,c)} = \gcd{(\gcd{(a,b)},c)} $$
でもこれだと式がめっちゃ汚くなる。そこで先ほどのアイディアが使えないかと考えてみる。
　$2$つの数では$2$次元の格子を使用したのだから、$3$つの数では$3$次元の格子を用いてみる。通る立方体の数は、交点個数$+1$より、次のように求められる。
$$ (a+b+c-\gcd{(a,b)}-\gcd{(b,c)}-\gcd{(c,a)}+\gcd{(a,b,c)})+1 $$
しかし問題は、どうしても立方体の個数を和表示できないのだ。おそらくはこの方針では解決不能であり、新しいアイディアが必要である。もしくは、和表示は$2$つの最大公約数に限った表示という考え方もできるかもしれない。