双曲線の性質とモジュラス付きAbelの定理
この記事では次の定理を証明します.
図のように双曲線$x^2-y^2=1$と円が各象限に1つずつ交点を持つとき、赤い部分と青い部分の面積は等しい.
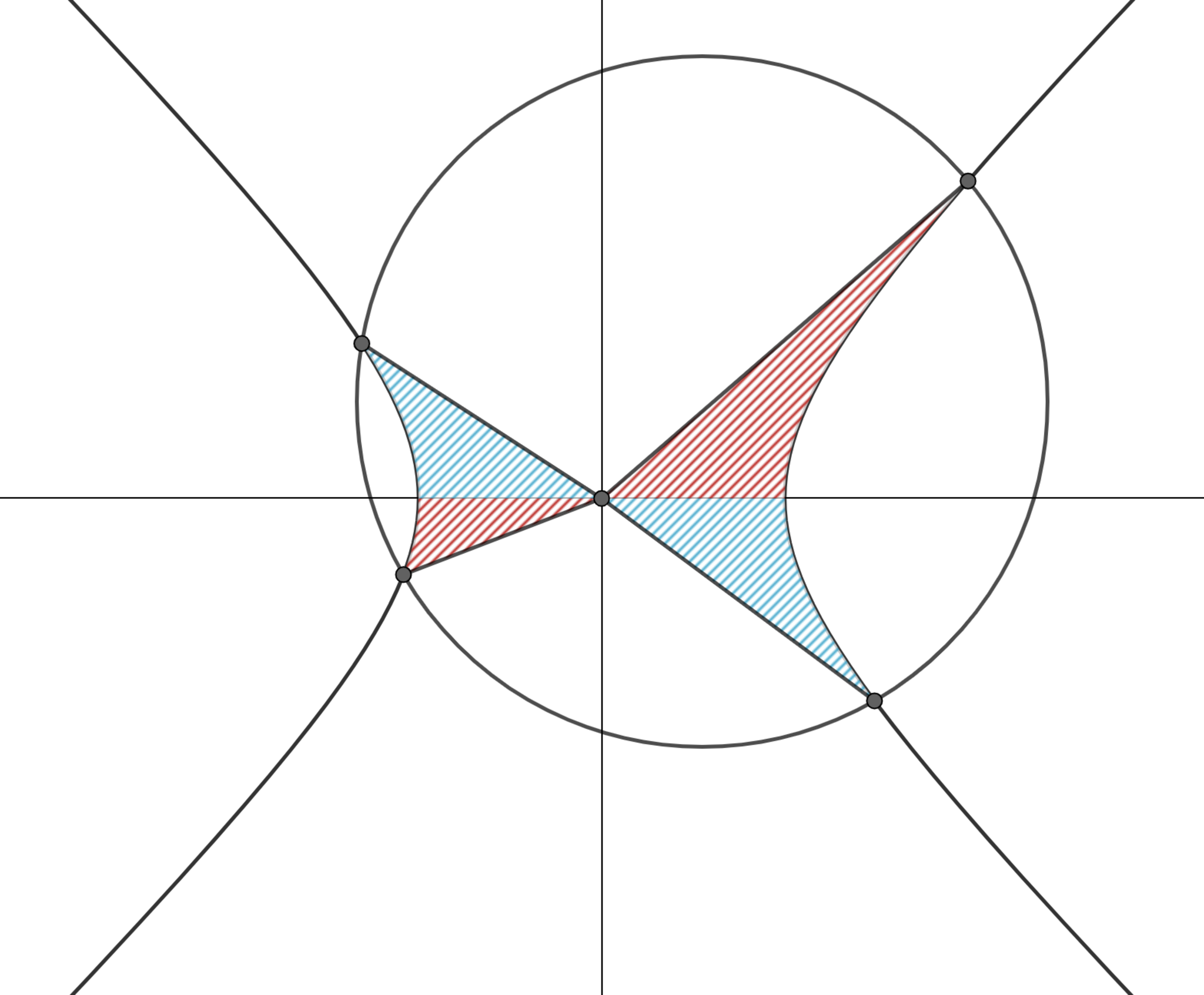
双曲線$x^2-y^2-1$上の点$P$に対し、$OP$と$x$軸および$x^2-y^2-1$で囲まれる部分の符号付き面積を$A(P)$と定めます(符号は奇数象限を正、偶数象限を負と定めます).実は定理1より強く次のことが成り立ちます:
双曲線$x^2-y^2=1$と円が重複を含めて4点$P_1,\dots,P_4$で交わるとき、$\sum_{i=1}^4A(P_i)=0.$
以下ではこの定理2のほうを証明します.
準備
$U$を$x^2-y^2=1$で定まる$\mathbb{C}^2$の閉部分集合とします.すると$U$には自然にRiemann面の構造が誘導されます.最初に考えていた双曲線は$U\cap \mathbb{R}^2$と表せますが、双曲線だけを考えるのではなく$U$全体を考える方が見通しよく証明ができます.この節では準備として$U$上の正則1形式とその積分について考えます.
$U$上の正則1形式の例として特に$\omega=\dfrac{dx}{y}$を考えましょう.$\omega$が実際に$U$上正則であることは、$U$のパラメータ表示$(x,y)=(\cosh z, \sinh z)$を用いると$\omega = dz$と書けることから分かります.このように表すと$\omega$はいかにも$U$上の代表的な微分形式のように見えます.実際あとで見るように、$U$上の正則1形式であって「無限遠に高々1位の極を持つ」ようなものは$\omega$の定数倍に限られます.
$U$上の任意の閉曲線$\gamma$に対して$\int_\gamma \omega\in 2\pi i\mathbb{Z}$が成り立つ.
Cauchyの積分定理より、$\int_\gamma\omega$の値は$\gamma$のホモロジー類のみで決まる.そこで$H_1(U,\mathbb{Z})$を求めよう.正則写像
$$
\mathbb{C}\to U; z\mapsto (\cosh z, \sinh z)
$$
は被覆写像であり同型$\mathbb{C}/2\pi i\mathbb{Z}\cong U$を誘導することが容易にわかる.よって$H_1(U,\mathbb{Z})\cong H_1(\mathbb{C}/2\pi i\mathbb{Z},\mathbb{Z})\cong\mathbb{Z}$であり、その生成元としては
$$
\gamma_0\colon [0,2\pi]\to U;~t\mapsto (\cos t, i\sin t)
$$
の類が取れることがわかる.$\int_{\gamma_0}\omega=2\pi i$なのでよい.
上の補題より、$U$上の2点$P,Q$を結ぶパス$\gamma,\gamma'$に対して
$$
\int_\gamma\omega = \int_{\gamma'}\omega\in \mathbb{C}/2\pi i\mathbb{Z}
$$
であることがわかります.そこでこの値を$\int_P^Q\omega\in \mathbb{C}/2\pi i\mathbb{Z}$と定めます.
定理の言い換え
実は冒頭に述べた$A(P)$の値は$U$上の積分を用いて表すことができます:
$P_0=(1,0)\in U$とすると、$P=(p,q)\in U\cap \mathbb{R}^2$に対して
$$
\int_{P_0}^P\omega=\begin{cases}
2A(P)&(p>0)\\
2A(P)+\pi i&(p<0).
\end{cases}
$$
まず$p>0,q>0$の場合を考える.$U$上で$x^2-y^2=1$であることに注意すると、$\omega$は$xdy-ydx$とも表すことができる.$U$上のパス$\gamma\colon [0,p]\to U$を$\gamma(t)=(t,\sqrt{t^2-1})$で定めると
$$
\int_{P_0}^P\omega=\int_\gamma\omega=\int_\gamma xdy-ydx
$$
となる.最後の表示が$2A(P)$に等しいことは容易にわかる.$p>0,q<0$の場合も同様である.
次に$p<0$の場合を考える.$P'_0=(-1,0)$とおくと、上と同様の計算により$\int_{P'_0}^P\omega=2A(P)$がわかる.一方、$U$上のパス$\eta\colon [0,\pi]\to U$を$\eta(t)=(\cos t,i\sin t)$で定めると
$$
\int_{P_0}^{P'_0}\omega=\int_\eta\omega=\pi i
$$
となる.これらを合わせれば主張が得られる.
これにより定理2の主張は「双曲線$x^2-y^2=1$と円が重複を含めて4点で交わるとき、交点にわたる$\int_{P_0}^P\omega$の総和は$0\in \mathbb{C}/2\pi i\mathbb{Z}$である」と言い換えられます.ここで$\Div(U)$を$U$上のWeil因子のなすAbel群とし、準同型$u\colon \Div(U)\to \mathbb{C}/2\pi i\mathbb{Z}$を
$$
u(\sum n_P[P])= \sum n_P\int_{P_0}^P\omega
$$
で定めます.上述のことから、定理2を示すには以下を示せば十分であることが分かります.
多項式$F(x,y)=(x-a)^2+(y-b)^2-c~(a,b,c\in \mathbb{R}, c>0)$に対して$u(\div(F))=0$である.
定理5では「双曲線と円が4点で交わる」という条件が無くなっていることに注意します.$U\cap \mathbb{R}^2$だけでなく$U$全体の上で交点を考えることで、このような不自然な条件を取り除くことができるわけです.
定理5の最も簡単な例として単位円を考えましょう.$F_0(x,y)=x^2+y^2-1$とすると$\div(F_0)=2[(1,0)]+2[(-1,0)]$であり、補題4より
$$
u(2[(1,0)]+2[(-1,0)])=0+2\pi i=0\in \mathbb{C}/2\pi i\mathbb{Z}
$$
なので、定理5は確かに成立しています.一般の$F(x,y)$に対しては$\div(F)=\div(F_0)+\div(F/F_0)$なので、定理4の主張は
$$
u(\div(F/F_0))=0
$$
と言い換えられます.ここで$X$を$\mathbb{P}^2$における$U$の閉包とすると、$X\setminus U$は2点$(1:\pm 1:0)$からなり、$F/F_0|_{X\setminus U}=1$となります.よって定理5を示すには次のことを示せば十分です.
$f\in k(X)^\times$が$f|_{X\setminus U}=1$を満たすならば$u(\div(f))=0$である.
証明
あとは定理6を示すのみとなりました.ここではまず直接的な方法を述べ、次節で「モジュラス付きAbelの定理」を用いた別証明を紹介します.
まず$X$と$\mathbb{P}^1$を
$$
\mathbb{P}^1\xrightarrow{\cong} X;~t\mapsto \biggl(\frac{t+t^{-1}}{2},\frac{t-t^{-1}}{2}\biggr)
$$
によって同一視します.この同型により$U$は$\mathbb{P}\setminus\{0,\infty\}$に対応し、$P_0\in X$は$1\in \mathbb{P}^1$に対応します.また$U$上の1形式$\omega$は$\mathbb{P}^1\setminus \{0,\infty\}$上の1形式$\dfrac{dt}{t}$に対応することも容易にわかります.
$$
\int_1^P\frac{dt}{t}=\log P\in \mathbb{C}/2\pi i\mathbb{Z}
$$
なので、定理6は次のように言い換えられます.
$f(0)=f(\infty)=1$を満たす有理式$f\in k(t)^\times$に対し、$\div(f)=\sum n_P[P]\in \Div(\mathbb{P}^1\setminus \{0,\infty\})$とおくと$\sum n_P\log P=0\in \mathbb{C}/2\pi i\mathbb{Z}$である.
$f(t)=\dfrac{a_nt^n+a_{n-1}t^{n-1}+\dots+a_0}{b_mt^m+b_{n-1}t^{n-1}+\dots+b_0}~(a_n,b_m\neq 0)$と表す.仮定$f(0)=f(\infty)=1$より$n=m,~a_n=b_n,a_0=b_0$が分かる.分子の零点を$P_1,\dots,P_n$とし、分母の零点を$Q_1,\dots,Q_n$とすると、解と係数の関係より
$$
P_1\dots P_n=(-1)^n\dfrac{a_0}{a_n}=(-1)^n\dfrac{b_0}{b_n}=Q_1\dots Q_n
$$
となる.$\div(f)=\sum_{i=1}^n[P_i]-\sum_{i=1}^n[Q_i]$であり、$\sum_{i=1}^n\log(P_i)-\sum_{i=1}^n\log(Q_i)=0\in \mathbb{C}/2\pi i\mathbb{Z}$なのでよい.
モジュラス付きAbelの定理
実は定理6は「モジュラス付きAbelの定理」というものの一例になっています.ここではその定理を紹介します.
$X$をコンパクトRiemann面とし、$D$を$X$上の有効因子、$U=X\setminus |D|$とします.このような組$(X,D)$をモジュラス付き曲線といい、$D$をそのモジュラスといいます.モジュラス付き曲線やその高次元版である「モジュラス対」を1つの幾何学的対象として扱う見方は、最近の代数幾何学や数論においても重要視されています.
さて、ここで$D$にのみ極を許した$X$上の有理型1形式の空間$H^0(X,\Omega_X(D))$を考えましょう.閉曲線に沿った積分により準同型
$$H_1(U,\mathbb{Z})\to H^0(X,\Omega_X(D))^\vee$$
が得られます.実はこの準同型は単射で、像は離散的であることが知られています.
$$
J_{X,D}=H^0(X,\Omega_X(D))^\vee/H_1(U,\mathbb{Z})
$$
と定め、$(X,D)$のGeneralized Jacobianといいます.$U$内の点$P,Q$を結ぶパス$\gamma,\gamma'$に対して
$$
\int_\gamma=\int_{\gamma'}\in H^0(X,\Omega_X(D))^\vee/H_1(U,\mathbb{Z})
$$
なので、この値を$\int_P^Q\in J_{X,D}$と定めます.さらに$P_0\in U$を固定し、準同型$u\colon \Div(U)\to J_{X,D}$を
$$
u(\sum n_P[P])=\sum n_P\int_{P_0}^P
$$
により定めます.$u$はAbel-Jacobi写像と呼ばれています.このとき次の定理が成り立ちます:
(1)$u$の核は$D$-principal divisorと$[P_0]$で生成される.ただし$D$-principal divisorとは、$f|_D=1$を満たす$f\in k(X)^\times$を用いて$\div(f)$と表せる因子のことを指す.
(2)$u$は全射である.
(1)はAbelの定理、(2)はJacobiの定理と呼ばれるものモジュラス付き版であり、いずれもRosenlichtによって示されました.ここではこの定理を認めた上で、(1)から定理6が従うことを説明します.
$U$を$x^2-y^2=1$で定まるRiemann面、$X$をその$\mathbb{P}^2$における閉包とし、$D=[(1:1:0)]+[(1:-1:0)]$とします.すると$X\cong \mathbb{P}^1$であることから$\Omega_X(D)\cong \mathcal{O}_X$がわかるので、$\dim H^0(X,\Omega_X(D))=1$となります.また$\omega = \dfrac{dx}{y}$はこの空間の基底をなしています.実際、同型$X\cong \mathbb{P}^1$によって$\omega$は$\dfrac{dt}{t}$に対応しますが、後者は$0$と$\infty$にのみ1位の極を持つことが容易にわかります.
よってこの場合$H^0(X,\Omega_X(D))^\vee\cong \mathbb{C}; \alpha\mapsto \alpha(\omega)$となります.また$H_1(X,\mathbb{Z})$の像は$2\pi i \mathbb{Z}\subset\mathbb{C}$に対応するので、$J_{X,D}\cong \mathbb{C}/2\pi i\mathbb{Z}$であり、Abel-Jacobi写像は
$$
u\colon \Div(U)\to \mathbb{C}/2\pi i\mathbb{Z};~\sum n_P[P]\mapsto \sum n_P\int_{P_0}^P\omega
$$
と同一視できます.以上より定理6が定理8(1)から従うことがわかります.
おまけ
ここに書いたのと同様の手法によって、次のような定理も示すことができます:
$F(x,y)$を$x^{d-i}y^i$($i$は奇数)の項を含まない$d$次多項式とする.$F(x,y)=0$と円$x^2+y^2=1$が重複を含めて$2d$個の点$\{(\cos \theta_i, \sin \theta_i)\}_{i=1}^{2d}$で交わるならば、$\sum_{i=1}^{2d}\theta_i=0\in \mathbb{R}/2\pi\mathbb{Z}$が成り立つ.
この定理から特に、$d$次関数のグラフ($d\geq 2$)と単位円が$2d$個の点で交わるとき、交点の偏角の総和は$0\in \mathbb{R}/2\pi\mathbb{Z}$であることがわかります.大雑把に言えば、$x^2-y^2=1$を全て$x^2+y^2=1$に置き換え、$\omega$を$-\dfrac{dx}{y}$に置き換えて上と同様の議論をすれば証明できます.ぜひ考えてみてください.