連続ウェーブレット変換
連続ウェーブレット変換
ウェーブレット解析の中でも基本的な, 連続ウェーブレット変換について解説します. この記事は, 参考文献にある私のノートから抜粋しました. より詳しい内容や参考文献の詳細はそちらをご覧ください.
What is a wavelet?
ウェーブレットという言葉を皆さん1度は耳にしたことがあると信じていますが, 何をしているのか分からない方は多いでしょう. ウェーブレットはスペルとしてはwaveletと書かれます. waveはもちろん波のことであり, letは小さいものを意味します. もっとも, これはフランス語のondeletteを英訳したときに出来た造語なのですが. ということで, ウェーブレット解析の主役は局在化された波となります.
ウェーブレットが研究され始めたのは1980年代であり, 数学にしては比較的新しい学問だと言えるでしょう. その発見はフランスの石油探査技師であったMorletに遡るのですが, このあたりのお話はあらゆる文献の序文に載っていますので割愛させてもらいます. ただ一言添えるのであれば, Morlet以前にもプロトタイプのウェーブレットは純粋数学や量子論, 工学分野などに存在していました. 分野の壁を壊すには時を待つしかなかったのです.
以上から, ウェーブレット解析とは局在化された波で関数や関数空間を解析する分野であると言えます. モチベーションは大事です.
通常, 周波数と言えばFourier変換を思い浮かべます. 確かに周波数だけを取り出すのであればFourier変換で十分ですが, 周波数が変化した瞬間の時間が特定できないことが欠点でした. その解決策として窓関数を掛けた窓Fourier変換が誕生しました. しかし, 窓関数は不確定性原理の影響を受けてしまいます（ちなみに, 最小不確定性を持つ窓関数であるGauss関数を窓にした場合はGabor変換と呼ばれます）. だったら, 最初から伸び縮みする小さな波を積分核にしよう, という発想がウェーブレット変換です. ちなみにウェーブレット変換にも不確定性原理は存在しますが, これは発展的話題です. このように時間と周波数を同時に解析する分野は時間周波数解析や超局所解析と呼ばれます.
さて, 早速定義に参りましょう.
連続ウェーブレット変換
Hilbert空間$L^2(\mathbb{R})$の関数$\psi$に対し, ウェーブレットを
$$
\psi_{ab}(x)=\frac{1}{\sqrt{|a|}}\psi \left( \frac{x-b}{a}\right),\quad a\in \mathbb{R}^*,\ b\in\mathbb{R}
$$
で定義する. ここで用いた関数$\psi$は特にマザーウェーブレットと呼ばれる.
定義から, マザーウェーブレット$\psi$を伸張パラメーター$a$と平行移動パラメーター$b$によって相似変形していることが分かりますね. 気になるのが係数ですが, これは$L^2$正規化$\|\psi_{ab}\|_{L^2}=\|\psi\|_{L^2}$のためであり, 通常は$\|\psi\|_{L^2}=1$と正規化されます.
関数$f\in L^2(\mathbb{R})$に対し, マザーウェーブレット$\psi$による連続ウェーブレット変換(CWT)を
$$
W_\psi [f](a,b)=\langle f,\psi_{ab}\rangle=\int_\mathbb{R} f(x)\overline{\psi_{ab}(x)}dx
$$
で定義する.
Schwarzの不等式により$|W_\psi [f](a,b)|\le \|f\|_{L^2}$であるので, CWTは有界作用素です.
有名なウェーブレットを2個だけ紹介しましょう.
マザーウェーブレット
$$
\psi_\sigma(x)= \frac{2\pi^{-1/4}}{\sqrt{3\sigma}}\left(1-\frac{x^2}{\sigma^2}\right)e^{-\frac{x^2}{2\sigma^2}}
$$
は幅$\sigma>0$のメキシカンハットウェーブレットと呼ばれる.
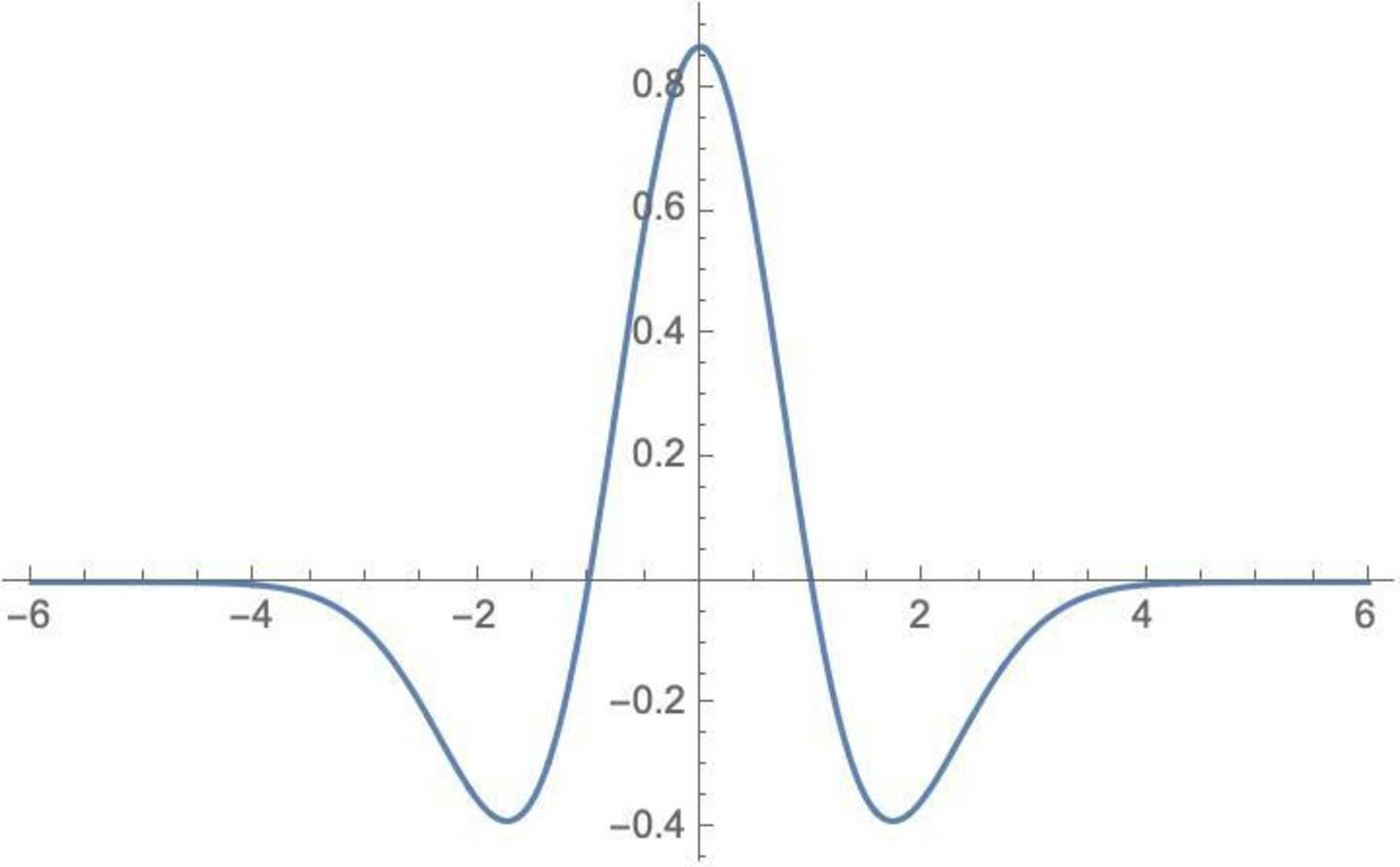幅1のメキシカンハットウェーブレット
マザーウェーブレット
$$
\psi(x)=\begin{cases}
1 & 0\le x< 1/2 \\
-1 & 1/2\le x<1
\end{cases}
$$
はHaarウェーブレットと呼ばれる.
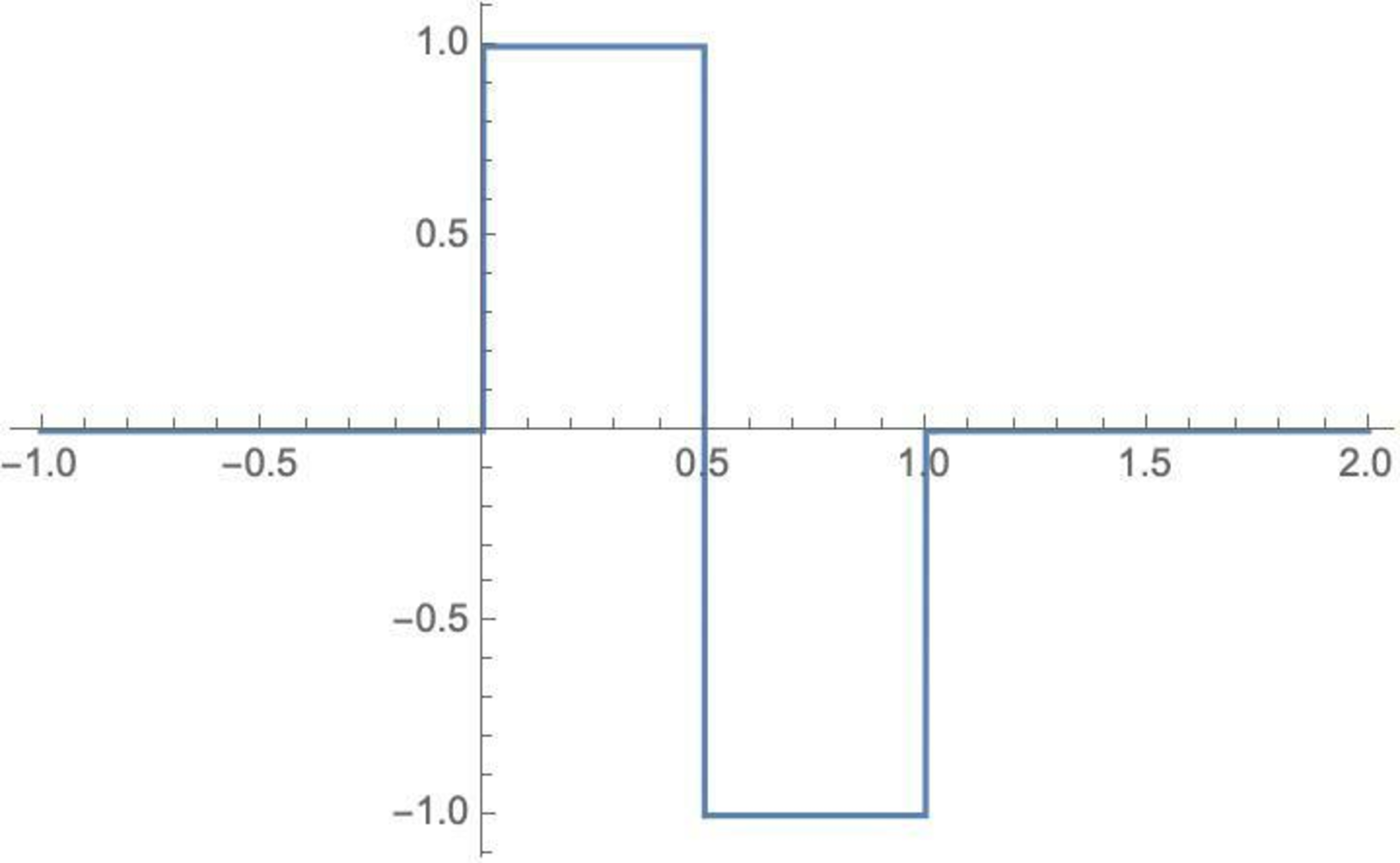Haarウェーブレット
ウェーブレット変換を視覚的に捉えるために, 数値実験をしてみましょう. サンプル関数として, 以下のチャープ信号を考えます:
![!FORMULA[17][852623417][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20210226164613.jpg?alt=media)
$f(x)=\sin(x^2)\quad\ 0\le x\le 10$
すると, 幅$1$のメキシカンハットウェーブレットを用いた$f$のCWT結果は以下になります（サンプル点数$10000$）:
![!FORMULA[21][37794][0]のCWT結果の絶対値プロット](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20210226165327.jpg?alt=media)
$f$のCWT結果の絶対値プロット
位置情報に関して激しく振動していることが読み取れます. ここで, 縦軸はスケール$a$ですが, 通常の座標軸と大小が逆転していることに注意してください. このように配置している理由は分野や趣味による影響が大きいのでしょうが, 逆スケール1/aが周波数成分に対応しているという事実からも来ています. 総合して, $f$の情報が視覚的に解析できました. このようなCWTの絶対値プロットをスケーログラムと呼びます.
逆連続ウェーブレット変換
関数変換を考えたならば, 逆変換も考えなければいけません. ということで, 逆連続ウェーブレット変換(ICWT)を定義しましょう. そのためにはマザーウェーブレットに対する制限が必要になります.
マザーウェーブレット$\psi$が許容条件を満たすということを
$$
C_\psi=\int_\mathbb{R} \frac{|\mathcal{F}[\psi](\xi)|^2}{|\xi|}d\xi<\infty
$$
で定義する. ここで, 作用素$\mathcal{F}$は1次元のFourier変換
$$
\mathcal{F}[f](\xi)=\hat f(\xi)=\int_\mathbb{R}f(x)e^{-ix\xi}dx
$$
である.
言わずもがな, Fourier変換には大きく3つの定義があり, どれを用いるかによって微妙な係数ずれが起きてくる. 勘弁してくれ...と言いたい気持ちを抑えつつ, 文献で用いられているFourier変換の定義を最初に確認しておこう.
次の関係式は単位の分解と呼ばれる.
許容条件を満たすマザーウェーブレット$\psi$に対し, 任意の$f,g\in L^2(\mathbb{R})$は以下を満たす:
$$
\frac{1}{C_\psi}\int_{\mathbb{R}^2} W_\psi [f](a,b)\overline{W_\psi [g](a,b)}\frac{da}{a^2}db=\langle f,g\rangle_{L^2}.
$$
Plancherelの定理から, CWTは
$$
W_\psi [f](a,b)=\frac{1}{2\pi}\int_\mathbb{R}\hat f(\xi) |a|^{\frac{1}{2}}e^{ib\xi}\overline{\hat \psi(a\xi)}d\xi
$$
と表せられるので,
$$
\begin{split}
I&:=\frac{1}{C_\psi}\int_{\mathbb{R}^2} W_\psi [f](a,b)\overline{W_\psi [g](a,b)}\frac{da}{a^2}db\\
&=\frac{1}{4\pi^2C_\psi}\int_{\mathbb{R}^2} \left(\int_\mathbb{R}\hat f(\xi) |a|^{\frac{1}{2}}e^{ib\xi}\overline{\hat \psi(a\xi)}d\xi\right)\overline{\left(\int_\mathbb{R}\hat g(\xi) |a|^{\frac{1}{2}}e^{ib\xi}\overline{\hat \psi(a\xi)}d\xi\right)}\frac{da}{a^2}db.\\
\end{split}
$$
さらに, Fubiniの定理とPlancherelの定理より,
$$
\begin{split}
I&=\frac{1}{C_\psi}\int_{\mathbb{R}}\frac{da}{a^2} \left\{\int_{\mathbb{R}} \mathcal{F}^{-1}_{\xi\to b}\left[\hat f(\xi) |a|^{\frac{1}{2}}\overline{\hat \psi(a\xi)} \right](b)\overline{\mathcal{F}^{-1}_{\xi\to b}\left[\hat g(\xi) |a|^{\frac{1}{2}}\overline{\hat \psi(a\xi)} \right](b)}db\right\}\\
&=\frac{1}{2\pi C_\psi}\int_{\mathbb{R}}\frac{da}{|a|} \int_{\mathbb{R}}\hat f(\xi)\overline{\hat \psi(a\xi)} \overline{\hat g(\xi)}\hat \psi(a\xi)d\xi.\\
\end{split}
$$
またFubiniの定理によって$a$に関してから積分し, $a\xi\to a'$の変数変換で,
$$
\begin{split}
I&=\frac{1}{2\pi C_\psi} \int_{\mathbb{R}}\hat f(\xi)\overline{\hat g(\xi)}d\xi\int_{\mathbb{R}}\frac{|\hat \psi(a\xi)|^2}{|a|}da\\
&=\frac{1}{2\pi C_\psi}\int_{\mathbb{R}}\frac{|\hat \psi(a')|^2}{|a'|}da' \int_{\mathbb{R}}\hat f(\xi)\overline{\hat g(\xi)}d\xi\\
&=\frac{1}{2\pi} \int_{\mathbb{R}}\hat f(\xi)\overline{\hat g(\xi)}d\xi\\
&=\langle f,g\rangle_{L^2}
\end{split}
$$
を得る.
直ちに次の結論を得ます.
弱収束の意味で以下の再生公式が成り立つ:
$$
f=\frac{1}{C_\psi}\int_{\mathbb{R}^2}W_\psi [f](a,b)\psi_{ab} \frac{da}{a^2}db.
$$
内積の連続性より,
$$
\langle f,g\rangle=\left\langle\frac{1}{C_\psi}\int_{\mathbb{R}^2} W_\psi [f](a,b)\psi_{a,b}\frac{da}{a^2}db,g\right\rangle
$$
が成り立つので明らか.
ICWTに出てきた測度
$$
d\mu=\frac{da}{a^2}db
$$
についての解釈の1つとしてHaar測度があります. 表現論の言葉を借りると, ウェーブレットは$ax+b$群のユニタリー表現$\psi\to\psi_{ab}$として見ることができます. そして, 測度$d\mu$は$ax+b$群の左Haar測度になっています. ここら辺の話題は抽象調和解析の主要テーマです.
実は強い意味でも等式が成り立ちます, 気が乗ったら証明してみてください.
参考文献
この記事を高評価した人
この記事に送られたバッジ
投稿者
