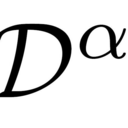(1+x+x^2)^8の係数で一番大きい数は？

【高校1～2年生レベル】

こんにちは。たしです。
今日はmathlogの練習も兼ねて、Twitterでふと見かけた次の問題を解説してみたいと思います。
https://twitter.com/wakara_nagomi/status/1324916988292947970?s=20

昼食をとってちょっとボーッとしたら頭の体操しましょう。

【問題】
次の式を展開したとき最も大きな係数は何でしょう？
計算機使うのは最後の手段です！(笑) pic.twitter.com/TtIhfPyzQ5

— 和から@大人のための数学・統計教室 (@wakara_nagomi) November 7, 2020

【問題】

$$ (1+x+x^2)^8 を展開したとき最も大きな係数は何か？ $$

【解答】

今回の解説では、答案として満点の解答というよりは、こう考えると簡単に解けるという大雑把な流れを解説するものになります。解答には大きく2つの流れがあります。

1. 係数が最大になるのは何次の項か求める。
2. 実際にその項の係数の値を求める。

1.係数が最大になるのは何次の項か？

解説にあたり、二項定理の組み合わせ的な解釈は知っていると仮定します。(多分高1レベル？)
二項定理を使うと、組み合わせの問題が多項式を展開した係数から求まってしまうのでした。例えば$(1+x)^2=1+2x+x^2$という結果からは、$「0」と「1」の2$面があるコインを2回投げた場合の組み合わせが求まります。
　　・2回とも「1」が出る 　　　　 → $x^2の係数=$ 1通り
　　・「0」と「1」が1回ずつ出る　→ $xの係数=$ 2通り
　　・2回とも「0」が出る 　　　　 → $1(=x^0)の係数=$ 1通り

この考えを使えば、例えばコインを100回投げて「1」の面が50回出る組み合わせは$(1+x)^{100}を展開したx^{50}$の係数、すなわち$_{100}C_{50}$と求まります。

以上を踏まえて、改めて最初の問題$(1+x+x^2)^8$を考えると、これは「0」「1」「2」が書かれた3面サイコロ(?)を8回振って和を求めることに対応します。このサイコロを1回振ったときの期待値は「1」なので8回振ったときの和の期待値は「8」だと考えられます。よって係数が最大となるのも8次の項$x^8$と言えます。
　　(※注)上の議論は感覚的なものであり、正確には数学的な証明が必要ですが割愛します。

2.最大になる項の係数の値は？

ここまでの議論で$(1+x+x^2)^8$の8次の項の係数が分かれば良いということが分かりました。では実際に展開して$x^8$の項が出てくるのはどのような場合が考えられるでしょうか。例えば『$x^2$を4回、$1(=x^0)$を4回かけた場合』や『$x^2$を2回、$x$を4回、$1$を2回かけた場合』などがあります。サイコロに戻して考えると前者の例は『「2」の目を4回、「0」の目を4回出した場合』に、後者は『「2」の目を2回、「1」の目を4回、「0」の目を2回出した場合』に相当します。これを元に和が「8」になる組み合わせを全て列挙すると次のようになります。

・「2」を4回、「0」を4回　　　　　　　→　$_8C_4 = 70通り$
　・「2」を3回、「1」を2回、「0」を4回　→　$_8C_3 \times _5C_2 = 560通り$
　・「2」を2回、「1」を4回、「0」を2回　→　$_8C_2 \times _6C_2 = 420通り$
　・「2」を1回、「1」を6回、「0」を1回　→　$_8C_1 \times _7C_1 = 56通り$
　・「1」を8回、　　　　　　　　　　　　 →　$_8C_8 = 1通り$

よって和が「8」になる組み合わせは、上の全ての場合を足し合わせて$1107通り(=70+560+420+56+1)$となります。これはすなわち$x^8$の係数が1107であるということでもあるので、求めるべき答えは『1107』となります。

念のため、実際に$(1+x+x^2)^8 $を展開してみると次のようになります。
$$ (1+x+x^2)^8 =1 + 8 x + 36 x^2 + 112 x^3 + 266 x^4+ 504 x^5 + 784 x^6 + 1016 x^7 + 1107 x^8 + 1016 x^9 + 784 x^{10} + 504 x^{11} + 266 x^{12} + 112 x^{13} + 36 x^{14} + 8 x^{15} + x^{16} $$
確かに係数が最大となるのは$x^8$のときで、その値は1107となっています。(式が見切れてたらごめんなさい！)

以上がTwitterで見かけた問題の解答になります。個人的にはこういう「組み合わせ」と「式の代数的操作」を行き来する問題は大好きです。読んでいただいた方の興味に少しでも刺されば幸いです。

もし誤植やミスがあった場合はコメントやTwitter(@math_lewisia)までお願いいたします。
それでは最後まで読んでいただきありがとうございました。