東大数学2021を実況する
はじめに
この記事では, 先日の, 東大数学2021を解いたときの頭の中の考え方を書いてみようと思います.
巷では東大らしからぬ問題だと言われていますね... 私もそう思いました🤔 まあでも出てしまったものは仕方がないので, 解くことにしましょう.
${}$
ちなむと, 私の点数は(論理で減点が多くなければ), [4]の(3)落としの100点くらいかなと思います. (得点開示でもっと低かったらごめんなさい😭)
時間配分は30/20/17/30/25/28 という感じでした.
${}$
それと先に言っておきたいのですが, 前回の記事で「計算するだけですね」などと申し上げましたが, 本番ですと緊張感が段違いなんですよね😱 軽はずみな発言は慎もうと思います...
では, 始めようと思います.
${}$
第1問
$\space$$a,b$を実数とする. 座標平面上の放物線
$$ C:\space y=x^2+ax+b$$
は放物線$y=-x^2$と$2$つの共有点をもち, 一方の共有点の$x$座標は$-1< x<0$を満たし, 他方の共有点の$x$座標は$0< x<1$を満たす.
$\space(1)$点$(a,b)$のとりうる範囲を座標平面上に図示せよ.
$\space(2)$放物線$C$の通りうる範囲を座標平面上に図示せよ.
なるほど... なんかまずは典型問題って感じがしますね🤔 とりあえず$(1)$は辺々引いて$f(x)$とかとおいて, 解の配置で$f(-1)>0,f(0)<0,f(1)>0$で終わりですね.
$(2)$は, あれれ...結構めんどくさくないですか??😢 逆像法的にやるのかなと思ったのですが場合わけの記述が面倒です...
でも求める範囲は, まあたぶん下の3通りが境界線になってるでしょうから, 地道にがんばりますか...
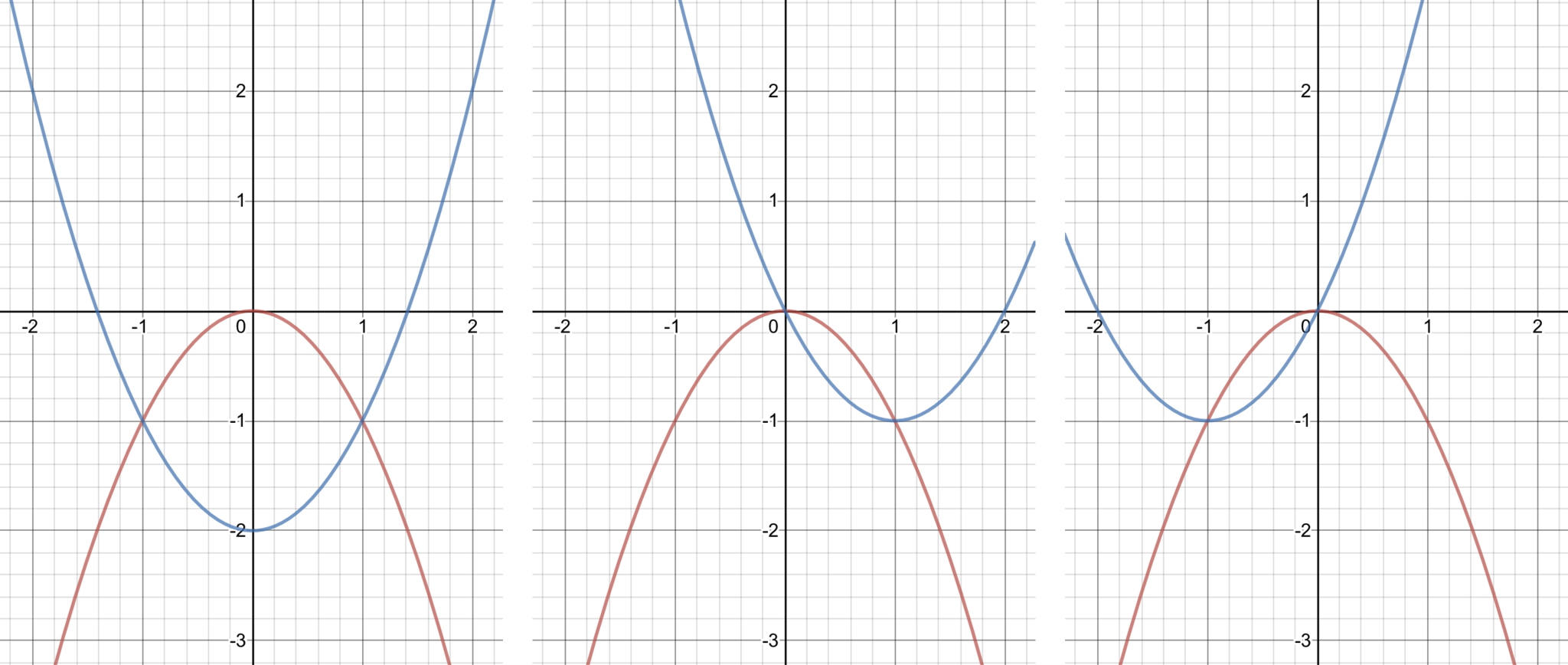 第1問
第1問
(とかいいつつ1回飛ばしてから戻ってきました...) 逆像法ちっくに, $(1)$の$(a,b)$の範囲と, $ab$平面の直線$b=-xa-x^2+y$が共有点を持つ$x,y$の条件, で解きました! $x<0$の部分はどうせ対照なので省略できます!
と, いうことで一応答えは出せましたが30分くらいかけちゃいました...😖
${}$
第2問
$\space$複素数$a,b,c$に対して整式$f(z)=az^2+bz+c$を考える. $i$を虚数単位とする.
$\space(1)$$\a,\b,\g$を複素数とする. $f(0)=\a, f(1)=\b, f(i)=\g$ が成り立つとき, $a,b,c$をそれぞれ$\a,\b,\g$で表せ.
$\space(2)$$f(0),f(1),f(i)$がいずれも$1$以上$2$以下の実数であるとき, $f(2)$のとりうる範囲を複素数平面上に図示せよ.
むむ... これもなんかよくわからない問題ですね🤔 そもそも$(1)$はただの連立方程式なんですけど...🙄 (このへんで, 今年はなにかがおかしいことに気づいてきました)
ということで$(2)$は, $(1)$の答えを代入すると
$$ f(2)=(-1-2i)\a+(3+i)\b+(-1+i)\g$$
なので, $1\leqq \a,\b,\g\leqq2$と動いた時のこれの値域を求めれば良いですね. こんなものは$f(2)=x+yi$とおいてベクトル的にやるのが良いです😤 誰かさんが仰っていたように, この問題は「複素数の無駄遣い」ですね...😖
さらに分かりやすいように, $\a=1+\a'$等とおくことで, $0\leqq \a',\b',\g'\leqq1$とできて, (こういうのも大事ですよね)
$$ \binom{x}{y}=\binom{1}{0}+\a'\binom{-1}{-2}+\b'\binom{3}{1}+\g'\binom{-1}{1}$$
となります. ここで$\g'$を固定すれば, これは点$(1-\g',\g')$を始点としてベクトル$\ds\binom{-1}{-2},\binom{3}{1}$の張る平行四辺形の内部となりますね. さらに$\g'$を動かすと始点が$(1,0)$から$(0,1)$と直線的に動くので, 以下のようだとわかりました🥰 箱みたいで面白いですね!😳
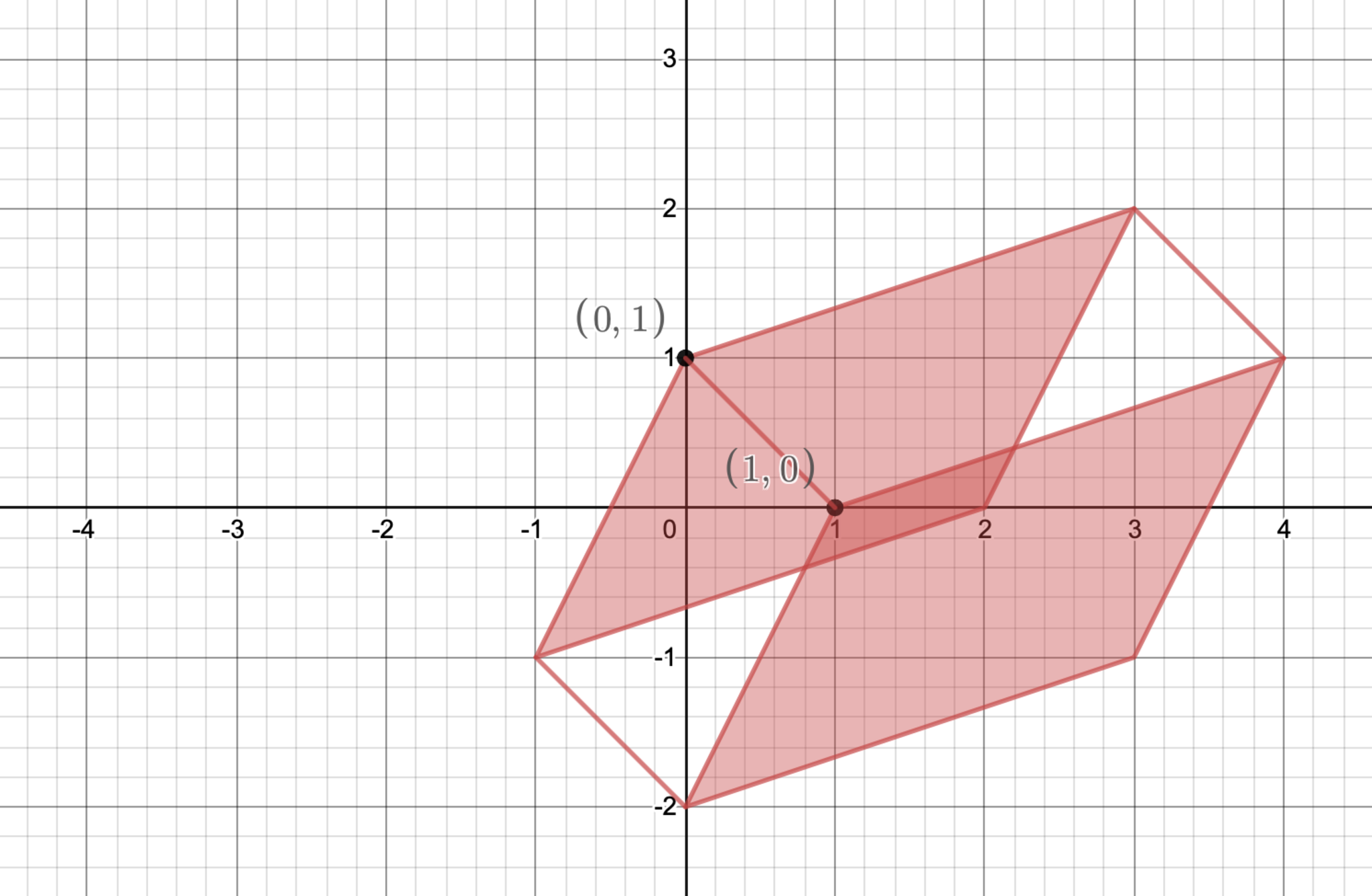 第2問
第2問
${}$
第3問
$\space$関数
$$ f(x)=\frac{x}{x^2+3}$$
に対して, $y=f(x)$のグラフを$C$とする. 点$\mathrm{A}(1,f(1))$における$C$の接線を
$$ \l:\space y=g(x)$$
とする.
$\space(1)$$C$と$\l$の共有点で$\mathrm{A}$と異なるものがただ$1$つ存在することを示し, その点の$x$座標を求めよ.
$\space(2)$$(1)$で求めた共有点の$x$座標を$\a$とする. 定積分
$$\int_\a^1\{f(x)-g(x)\}^2\,dx$$
を計算せよ.
わぁ, なんか定期試験にありそうな問題です...🤭 $(2)$は単純計算するしかなさそうですし...
まあ$(1)$は†計算するだけ†ですね. $g(x)=\dfrac18(x+1)$で, $\a=-3$です.
ところが$(2)$も†計算するだけ†ですね... これは怖かったので私は1回飛ばしました...😖
とりあえず$(1)$の流れからいくとまず通分して$f(x)-g(x)=-\dfrac{(x-1)^2(x+3)}{8(x^2+3)}$としたくなりますが, これは罠です!!! これだと2乗したあとに次数下げが面倒なだけなので, 通分しないで2乗すると良いです☺️ あとはもう自分の計算力を信じるしかないですね💪
${}$
第4問
$\space$以下の問いに答えよ.
$\space(1)$正の奇数$K,L$と正の整数$A,B$が$KA=LB$を満たしているとする. $K$を$4$で割ったあまりが$L$を$4$で割った余りと等しいならば, $A$を$4$で割った余りは$B$を$4$で割った余りと等しいことを示せ.
$\space(2)$正の整数$a,b$が$a>b$を満たしているとする. このとき, $A=\c{4a+1}{4b+1},B=\c{a}{b}$に対して$KA=LB$となるような正の奇数$K,L$が存在することを示せ.
$\space(3)$$a,b$は$(2)$の通りとし, さらに$a-b$が$2$で割り切れるとする. $\c{4a+1}{4b+1}$を$4$で割ったあまりは$\c{a}{b}$を$4$で割った余りと等しいことを示せ.
$\space(4)$$\c{2017}{37}$を$4$で割った余りを求めよ.
難しそうな整数問題です...! でも$(4)$は割と面白そうなので, やっていきましょう.
まあ$(1)$は$K\equiv L\equiv1$のときは自明で, $K\equiv L\equiv3$のときは$4A\equiv4B$を辺々引けば良いんですかね〜🤔
$(2)$は, わあ, 難しいです......😖 とりあえず1回飛ばして戻ってきて考えたら, $BA\equiv AB$の両辺を2で何回か割って$B$が$K$に, $A$が$L$になれば良さそうなので, やっぱり$2$で割れる回数が同じなんですかね...
そしたら例の, $n!$が素数$p$で割れる回数は$\ds\sum_{k=0}^\infty\left\lfloor\frac{n}{p^k}\right\rfloor$ だっていうやつを使えば良いんですかね〜, Cは!で表せますからね.
$(3)$は本当に, I have no idea です...😖 10分くらい考えましたがわかりませんでした😢 (未だに分かりません...) 後から聞いたところによると, 2で割れる回数と違う考え方をしないといけないようですね〜.
あとはもう$(4)$は答えだけ書いて点数をもらいにいきました.
${}$
第5問
$\space$$\a$を正の実数とする. $0\leqq \t \leqqπ$における$\t$の関数$f(\t)$を, 座標平面上の$2$点$\mathrm{A}(-\a,-3),\mathrm{P}(\t+\sin\t,\cos\t)$間の距離$\mathrm{AP}$の$2$乗として定める.
$\space(1)$$0<\t<π$の範囲に$f'(\t)$となる$\t$がただ$1$つ存在することを示せ.
$\space(2)$以下が成り立つような$\a$の範囲を求めよ.
$\space$$0\leqq \t \leqqπ$における$\t$の関数$f(\t)$は, 区間$0<\t<\dfracπ2$のある点において最大になる.
これは... なんなんですかね🤔 とりあえず$(1)$は微分する以外に示しようがないですよね...
$(1)$ 面倒な式は書きませんが, 計算すると以下の表のようになりました. ($f''$の時点でうまくいきそうになかったので$f'''$までやりました) (+)は正の値, (-)は負の値を表します.
| $0$ | $\dfracπ2$ | $π$ | |
|---|---|---|---|
| $f'$ | (+) | ? | $0$ |
| $f''$ | $0$ | (-) | (+) |
| $f'''$ | (-) | $0$ | (+) |
$f'''$の符号から, $f''$が$0$から負になってから正になるので, ただひとつ$f(\b)$なる$\dfracπ2<\b<π$がありますから, 以下のようになります.
| $0$ | $\cdots$ | $\dfracπ2$ | $\cdots$ | $\b$ | $\cdots$ | $π$ | |
|---|---|---|---|---|---|---|---|
| $f'$ | (+) | $\searrow$ | ? | $\searrow$ | (-) | $\nearrow$ | $0$ |
| $f''$ | $0$ | $\searrow$ | (-) | $\nearrow$ | $0$ | $\nearrow$ | (+) |
| $f'''$ | (-) | (-) | $0$ | (+) | (+) | (+) | (+) |
なので, $0$と$\b$の間で$f'$は$0$となるっていうことですね.
$(2)$は$f'$が単調な感じなので, $f'(\hp)<0$っていうだけですね. あっけないです🤭
${}$
ちなみにこの問題, 図形的にも理解することができます! $\mathrm{P}$の軌跡はサイクロイドになり, $f'=0$というのは$\mathrm{AP}$の距離の停留点ですので, $\mathrm{AP}$が$\mathrm{P}$でのサイクロイドの法線になっているんですね.
つまり$(2)$の$\a$の境界は, サイクロイドの$\t=\hp$の点での法線と$y=-3$の交点になっているというのが種明かしでした!😚
${}$
第6問
$\space$定数$b,c,p,q,r$に対し,
$$ x^4+bx+c=(x^2+px+q)(x^2-px+r)$$
が$x$についての恒等式であるとする.
$\space(1)$$p\neq0$であるとき, $q,r$を$p,b$で表せ.
$\space(2)$$p\neq0$とする. $b,c$が定数$a$を用いて
$$ b=(a^2+1)(a+2),\space c=-\left(a+\dfrac34\right)(a^2+1)$$
と表されているとき, 有理数を係数とする$t$についての整式$f(t)$と$g(t)$で
$$ \{p^2-(a^2+1)\}\{p^4+f(a)p^2+g(a)\}=0$$
を満たすものを$1$組求めよ.
$\space(3)$$a$を整数とする. $x$の$4$次式
$$ x^4+(a^2+1)(a+2)x^2-\left(a+\dfrac34\right)(a^2+1)$$
が有理数を係数とする$2$次式の積に因数分解できるような$a$をすべて求めよ.
これもよくわからないですね...🤔 まあ$(3)$が少し面白い結果になるのでしょうか.
とりあえず$(1)$は係数比較で$\ds q=\frac12\Big(p^2-\frac{b}{p}\Big),r=\frac12\Big(p^2+\frac{b}{p}\Big)$ですね.
$(2)$は, え, どういうことですか???😖 まずなんで$p^2-(a^2+1)$がついてるのかわかんないのですが...🤔
あ, しばらく考えたら分かりました! $b,c$を$a$で定めたので, それを一番最初の式に代入して, $p$と$a$の関係式を出せっていうことなんですかね! そしたら$(1)$で使わなかった定数項の比較から, $c=qr$ にいろいろ代入すれば
$$ -(4a+3)(a^2+1)=p^4-\frac{b^2}{p^2}$$
となって$p$の$6$次式が出てくるので, これが問題分のように因数分解できるんですね〜🤔 すこし求められていることを忖度しないといけませんでした😔
$(3)$はあとは, $(2)$の式の$a$が整数, $p$が有理数である解を見つけるということですね〜. なかなか難しそうです😖
と思って戻ってきたら, 2つめの因数は常に正ではないですか!!!そうすると1つめの方の解で, $a=0$だけしかないですね... あ, $p=0$のパターンも, と思ったらそれは$b=0$で$a=-2$なので$x^4+\frac{25}{4}$になって明らかにできないですね...
じゃあやっぱり答えは$a=0$だけなのでしょうか?不安でしかたありません...😢
${}$
おわりに
今回は結構長くなってしまいました😖
問題は, ほんとうに定期試験のような問題が多くて🤔🤔🤔でしたね... 面白さがあんまりなかったです.
それと, どの大問も$(1)$がめちゃくちゃに簡単なので([5]を除く), 低得点層の方にとっては易化, 高得点層にとっては難化っていう感じですかね〜🤭
まあ, もう入試は終わったことですし, 特例追試の問題でも楽しみにしながら, 今回はこのへんで終わろうと思います.
ここまで読んで下さった方, ありがとうございました.
${}$
