自作問題置き場(OMC)

OMC で出題した私の問題をまとめます．(随時更新します(多分)) 　

OMC007D(分野：N)

正の整数 $n_1\ge n_2\ge \cdots \ge n_{2020}$ について, $x$ の $4040$ 次方程式
$$(x^2-n_{1}x+n_2)(x^2-n_{2}x+n_3)\cdots (x^2-n_{2019}x+n_{2020})(x^2-n_{2020}x+n_1)=0$$
の解が全て正の整数となるとき, $n_1$ の取りうる値の総和を求めてください.

OMC011D(分野：G)

$AB=2,BC=1,CA=\sqrt{3}$ である三角形 $ABC$ の内心を $I$ とします. 点 $P$ が辺 $AB$ 上を, 点 $Q$ が辺 $BC$ 上を, 点 $R$ が辺 $CA$ 上をそれぞれ動くとき, $IP+PQ+QR+RI$ のとり得る最小値は正の整数 $a,b,c$ を用いて $\sqrt{a-b\sqrt{c}}$ と表わされます. $a+b^{2}c$ を求めてください.

OMC013C(分野：N)

複素数 $x$ についての方程式 $x^2-2(m-480)+(4m+97)=0$ が, 正整数解のみを持つような整数 $m$ について, その総和を求めてください.

OMC013E(分野：A)

$15$ 個の式
$$\begin{array}{r}\{\begin{array}{l}{x}_1^2+x_2+x_3+\cdots +x_{15}=1\\ x_1+x_2^2+x_3+\cdots +x_{15}=1\\ x_1+x_2+x_3^2+\cdots +x_{15}=1\\ ⋮\\ x_1+x_2+x_3+\cdots +x_{15}^2=1\end{array}\end{array}$$
を満たす実数の組 $(x_1,x_2,\cdots ,x_{15})$ の個数を求めてください.

OMC014B(分野：N)

$2021$ は次の性質を持つ $4$ 桁の正整数です.

• $100$ で割った余りは $100$ で割った商より $1$ 大きい
• $2021=43\times 47$ のように, 差が $4$ である $2$つの正整数の積で表すことができる
  この $2$ つの性質をもつ $2021$ 以外の $4$ 桁の正整数をすべて求めてください.

OMC014D(分野：N)

次の条件を満たす $100$ 以下の正の偶数 $n$ の総和を求めてください.

• $n<pq$ かつ $(p-1{)}^{q-1}+(q-1{)}^{p-1}\equiv n(\mathrm{mod}pq)$ を満たす素数の組 $(p,q)$ が存在する.

OMC014E(分野：C)

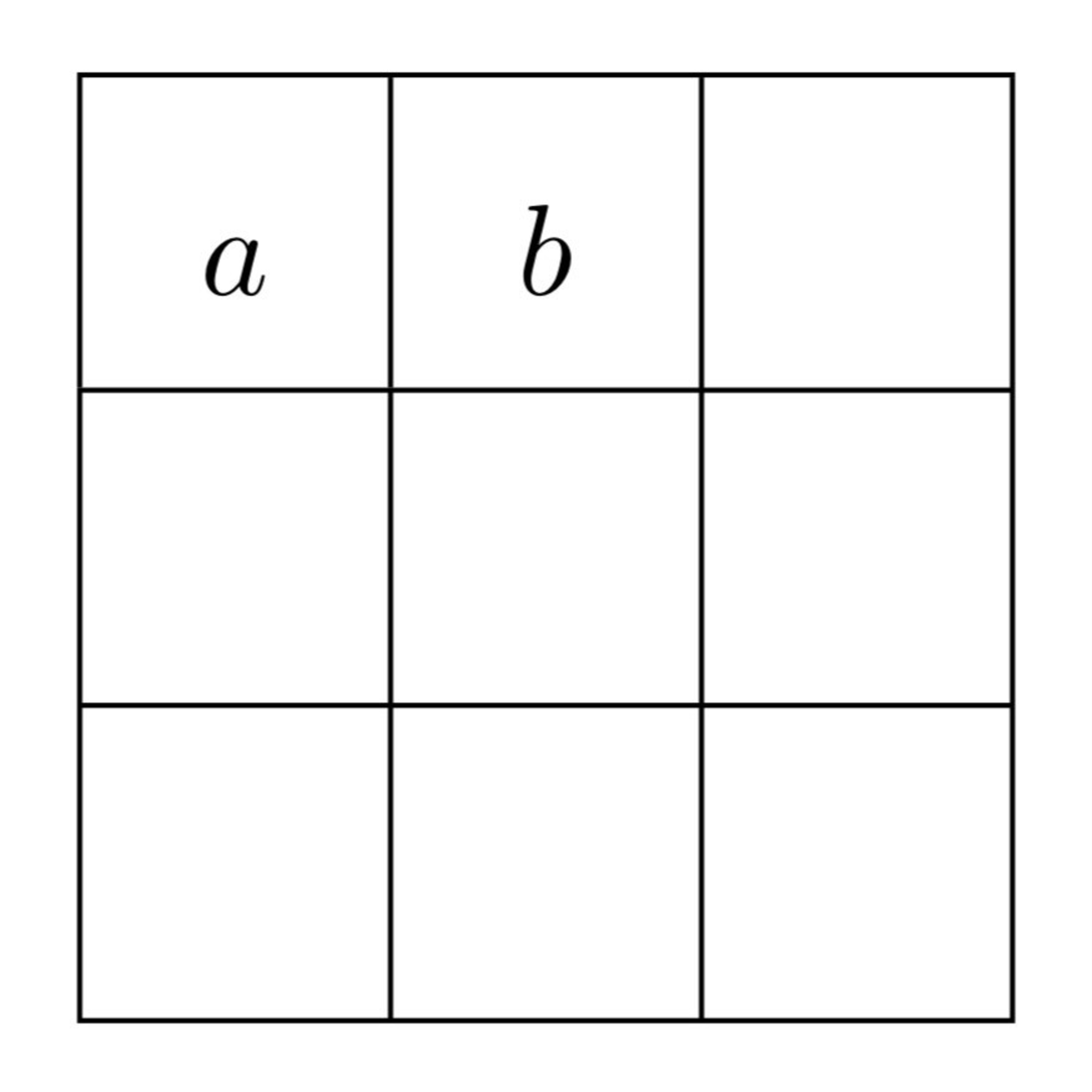
$3\times 3$ のマス目の各マスに, 正整数を入れていくことを考えます. いま, 図のように $2$ つの正整数 $a,b$ が既に埋まっています. このとき, 他の $7$ マスについて, 次の条件を満たす正整数の入れ方がちょうど $2021$ 通り存在しました.

• $3\times 3$ のマス目が魔法陣となる. すなわち, 各行, 各桁, 各対角線上にある $3$ つの下図の和は全て等しくなる.

$a,b\le {10}^6$ の範囲で, このような正整数の組 $(a,b)$ の個数を求めてください.

OMC016B(分野：C)

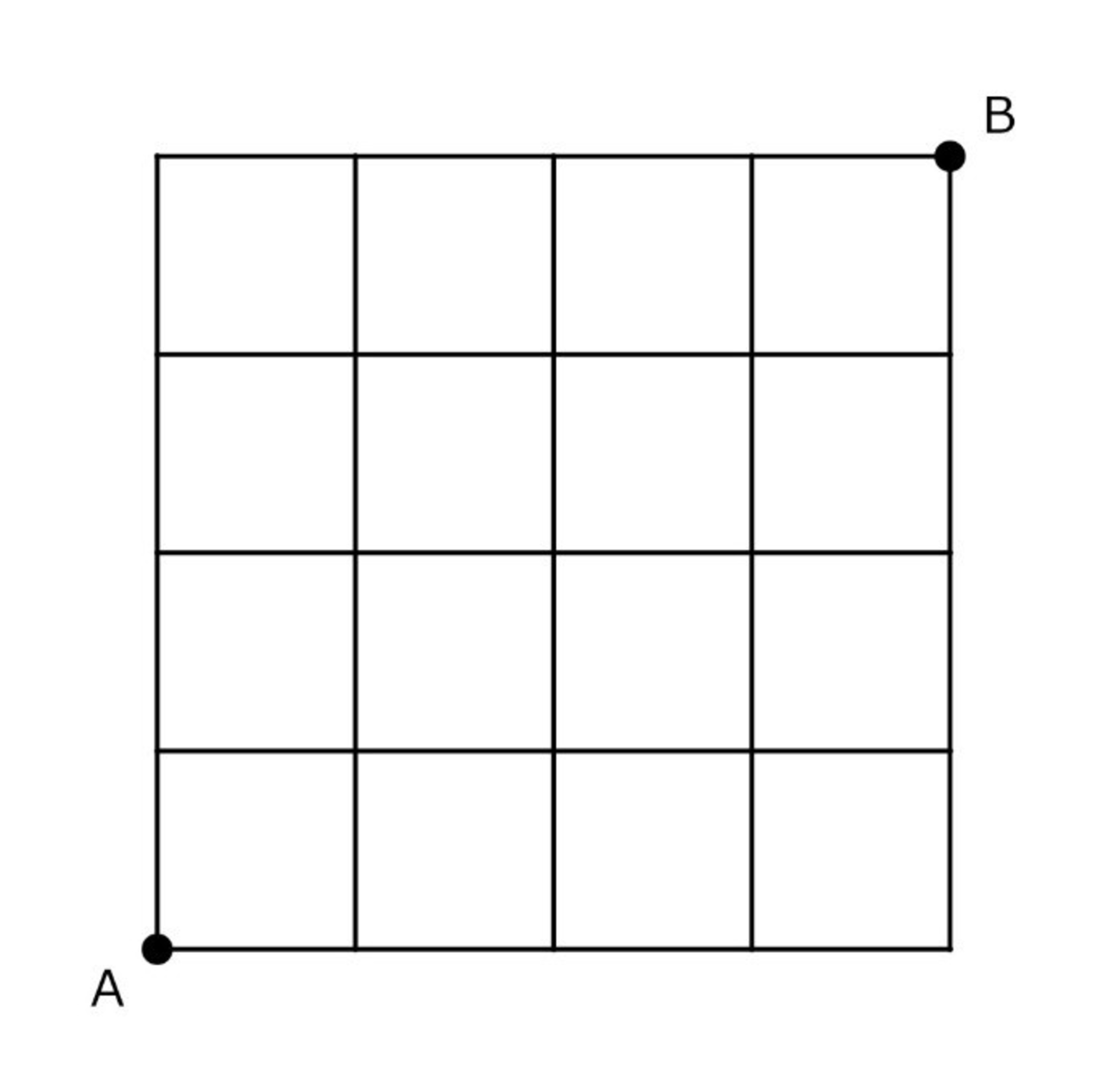
下図のような碁盤の目状の道があります. 図で示された $40$ 区間を除いて道は存在しません.
　torii君は地点 $A$ から地点 $B$ まで歩いていくことになりましたが, 途中で迷子になってしまい, 初めて $B$ 地点に到達するまでちょうど $10$ 区間歩きました. torii君が歩いた経路として考えられるものは何通りありますか.
　ただし, torii君は直前に通った区間を逆向きに引き返しても良いですが, 区間の中途では引き返せません.

OMC020C(分野：C)

正の整数 $n$ が $k$ 桁の良い数であるとは, 次の条件をみたすことを指します. \

• $n$ を $10$ 進法表記で $\overline{a_1{a}_2\cdots a_{k-1}{a}_k}$ と表したとき, ある整数 $N(1<N<k)$ が存在して以下が成立する. ただし各 $i=1,\cdots ,k$ について $0\le a_i\le 9$ であり, 特に $a_1\ne 0$ である. $$a_1<a_2<\cdots <a_{N-1}<a_N>a_{N+1}>\cdots >a_{k-1}>a_k$$

例えば $12321$ や $1357986420$ は良い数ですが, $123321$ や $12345$ は良い数ではありません.

$10$ 進法表記で $15$ 桁の良い数であって, $3$ の倍数であるものの個数を求めてください.

OMC020D(分野：N)

次の条件を満たす正整数 $N$ のうち，$5$ 番目に小さいものを $1000$ で割った余りを求めてください．

• $a<b$かつ${\displaystyle \sum _{k=a}^{b}k=N}$ なる相異なる正整数の組 $(a,b)$ が, ちょうど $2021$ 組存在する．

OMC022E(分野：G)

正三角形 $ABC$ において, その内部の点 $P$ が以下の等式をみたしました.
$$A{P}^2+B{P}^2=A{B}^2,B{P}^2+C{P}^2=A{P}^2$$
このとき, 三角形 $PAB,PBC,PCA$ の面積比を求めてください.