積分botを解けるだけ解く, その1

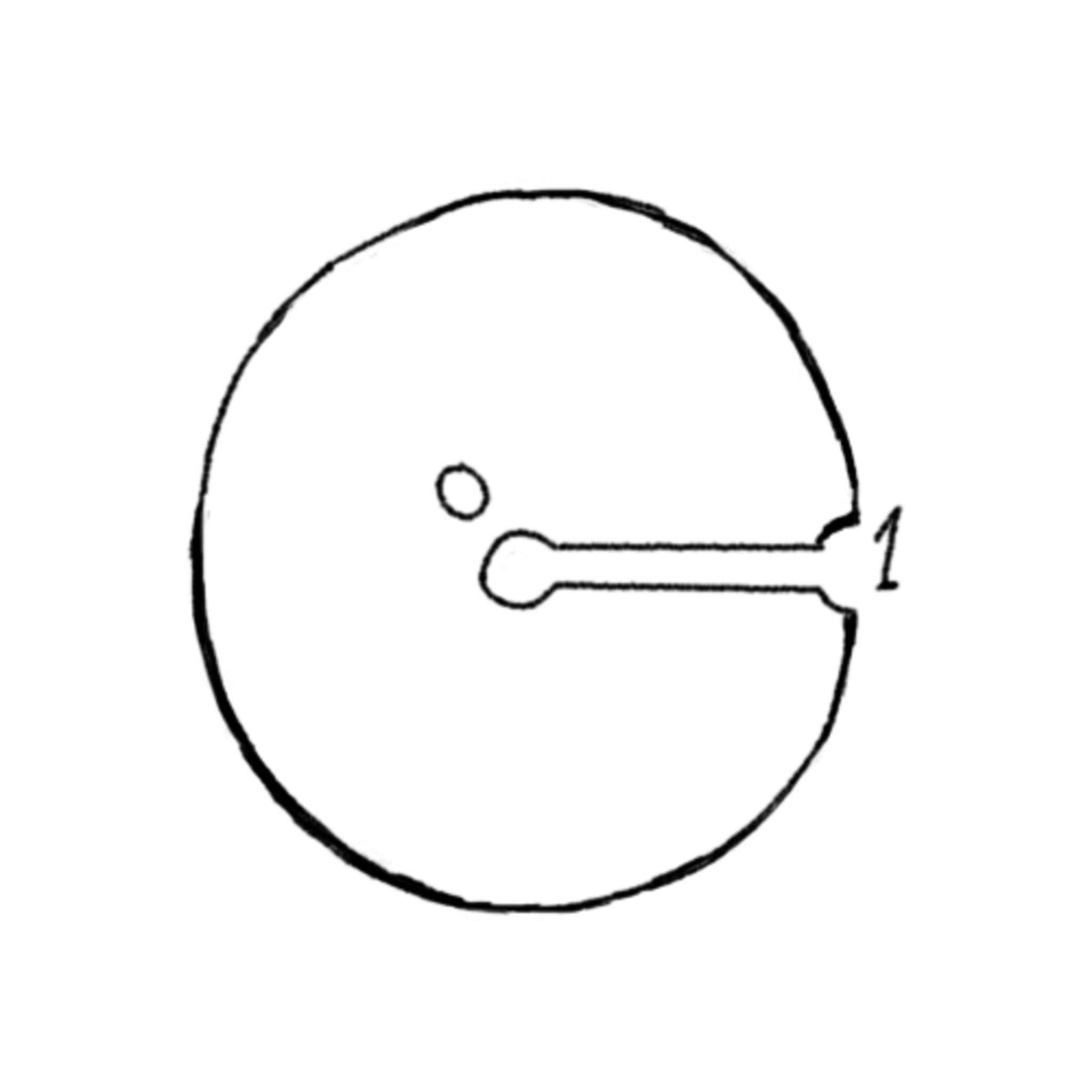積分路1

上のような積分路$C$を考えます.

$$\begin{eqnarray*} \int_Cx^{a-1}(1-x)^{b-1}\,dx&=&(1-e^{2\pi ia})\int_0^1x^{a-1}(1-x)^{b-1}\,dx+i\int_0^{2\pi}e^{iax}(1-e^{ix})^{b-1}\,dx\\ &=&-2ie^{i\pi a}B(a,b)\sin\pi a-e^{-i\pi b/2}\int_0^{2\pi}e^{i(a+(b-1)/2)x}\left(2\sin\frac x2\right)^{b-1}\,dx \end{eqnarray*}$$

一方, $\ln$の主値は上の曲線内で$1$価正則に取れるので, この積分は$0$になります. よって,

$$\begin{eqnarray*} \int_0^{2\pi}e^{i(a+(b-1)/2)x}\left(2\sin\frac x2\right)^{b-1}\,dx&=&2e^{i\pi (a+(b-1)/2)}B(a,b)\sin\pi a\\ &=&\frac{2\pi\Gamma(b)e^{i\pi(a+(b-1)/2)}}{\Gamma(1-a)\Gamma(a+b)} \end{eqnarray*}$$

$a\mapsto \frac{1-b+c}2$と置き換えて,
$$\begin{eqnarray*} \int_0^{2\pi}e^{icx/2}\left(2\sin\frac x2\right)^{b-1}\,dx&=&\frac{2\pi\Gamma(b)e^{i\pi c/2}}{\Gamma\left(\frac{1-c+b}{2}\right)\Gamma\left(\frac{1+c+b}2\right)}\\ \int_0^{\pi}e^{icx}\sin^{b-1} x\,dx&=&\frac{2^{1-b}\pi\Gamma(b)e^{i\pi c/2}}{\Gamma\left(\frac{1-c+b}{2}\right)\Gamma\left(\frac{1+c+b}2\right)} \end{eqnarray*}$$
この虚部を考えることにより, 証明ができました.

$$\begin{eqnarray*} \ln\frac{1+ax}{1-ax}=2\sum_{0\leq n}\frac{(ax)^{2n+1}}{2n+1} \end{eqnarray*}$$
なので, 項別に積分していくと,
$$\begin{eqnarray*} \int_0^1\ln\frac{1+ax}{1-ax}\frac{dx}{x\sqrt{1-x^2}}&=&\sum_{0\leq n} \frac{2}{2n+1}a^{2n+1}\int_0^1x^{2n}(1-x^2)^{-1/2}\,dx\\ &=&\sum_{0\leq n}\frac{a^{2n+1}}{2n+1}\int_0^1x^{n-1/2}(1-x)^{-1/2}\,dx\\ &=&\sum_{0\leq n}\frac{a^{2n+1}}{2n+1}\frac{\Gamma\left(\frac 12\right)\Gamma\left(\frac 12+n\right)}{\Gamma(n+1)}\\ &=&\pi\sum_{0\leq n}\frac{\left(\frac 12\right)_n}{n!(2n+1)}a^{2n+1}\\ &=&\pi\arcsin a \end{eqnarray*}$$
となって証明ができました.

$$\begin{eqnarray*} \int_{-\infty}^{\infty}\ln(2-2\cos x^2)\,dx&=&2\int_0^{\infty}\ln(2-2\cos x^2)\,dx\\ &=&4\int_0^{\infty}\ln\left|2\sin\frac {x^2}2\right|\,dx\\ &=&2\int_0^{\infty}x^{-1/2}\ln\left|2\sin\frac x2\right|\,dx \end{eqnarray*}$$
$0\lt \Re s$として,
$$\begin{eqnarray*} \int_0^{\infty}x^{s-1}\ln(1-e^{-ix})\,dx&=&-\sum_{0\lt n}\frac 1n\int_0^{\infty}x^{s-1}e^{-inx}\,dx\\ &=&-i^{-s}\Gamma(s)\sum_{0\lt n}\frac 1{n^{s+1}}\\ &=&-i^{-s}\Gamma(s)\zeta(s+1) \end{eqnarray*}$$
$s=\frac 12$として, これの実部をとることにより,
$$\begin{eqnarray*} 2\int_0^{\infty}x^{-1/2}\ln\left|2\sin\frac x2\right|\,dx=-\sqrt{2\pi}\zeta\left(\frac 32\right) \end{eqnarray*}$$
を得ます.

$$\begin{eqnarray*} \int_0^{\infty}x^{s-1}(\cos x^2-\cos x)\,dx&=&\frac 12\Gamma\left(\frac s2\right)\cos\frac{\pi s}{4}-\Gamma(s)\cos\frac{\pi s}{2}\\ &=&\frac 12\left(\frac 2s-\gamma+O(s)\right)(1+O(s^2))-\left(\frac 1s-\gamma+O(s)\right)(1+O(s^2))\\ &=&\frac{\gamma}{2}+O(s) \end{eqnarray*}$$
ここで, $s\to +0$とすればよい.

まず, 少し準備をします.
$$\begin{eqnarray*} \int_0^{\infty}\frac 1{(1+x^2)(1+a^2x^2)}\,dx&=&\frac 1{1-a}\int_0^{\infty}\left(\frac{1}{1+x^2}-\frac{a^2}{1+a^2x^2}\right)\,dx\\ &=&\frac{\pi}{2(1+a)} \end{eqnarray*}$$
となります. ここから, ある定数$C$があって,
$$\begin{eqnarray*} \int_0^{\infty}\frac{\arctan ax}{x(1+x^2)}\,dx=\frac{\pi}{2}\ln(1+a)+C \end{eqnarray*}$$
となりますが, $a=0$として, $C=0$を得ます.
$$\begin{eqnarray*} \int_0^{\infty}\frac{\arctan ax}{x(1+x^2)}\,dx=\frac{\pi}{2}\ln(1+a) \end{eqnarray*}$$
これを用いて, 与えられた積分を考えていきます.

$$\begin{eqnarray*} &&\int_0^{\pi/2}\frac 1{\tan x}\ln\left(\frac{1+(\tan x+\sinh y)^2\cosh^2y}{1+(\tan x-\sinh y)^2\cosh^2 y}\right)\,dx\\ &=&\int_0^{\infty}\frac{1}{x(1+x^2)}\ln\left(\frac{1+(x+\sinh y)^2\cosh^2 y}{1+(x-\sinh y)^2\cosh^2 y}\right)\,dx\\ &=&2\int_0^{\infty}\frac{1}{x(1+x^2)}\ln\left|\frac{1+i((\sinh y+x)\cosh y)}{1+i((\sinh y-x)\cosh y)}\right|\,dx\\ &=&2\Re\int_0^{\infty}\frac 1{x(1+x^2)}\ln\left(\frac{1+i((\sinh y+x)\cosh y)}{1+i((\sinh y-x)\cosh y)}\right)\,dx\\ &=&-4\Re\left( i\int_0^{\infty}\frac 1{x(1+x^2)}\arctan\left(\frac{x\cosh y}{1+i\sinh y\cosh y}\right)\,dx\right)\\ &=&4\Im\left(\frac{\pi}{2}\ln\left(1+\frac{\cosh y}{1+i\sinh y\cosh y}\right)\right)\\ &=&2\pi\arctan\left(\frac{\sinh y\cosh^2 y}{1+\cosh y+\sinh^2 y\cosh^2 y}\right) \end{eqnarray*}$$
となりました.

Binetの第2公式
$$\begin{eqnarray*} \ln\Gamma(z)=\frac 12\ln 2\pi+\left(z-\frac 12\right)\ln z-z+2\int_0^{\infty}\frac{\arctan\frac{x}{z}}{e^{2\pi x}-1}\,dx \end{eqnarray*}$$
を二階微分すると,
$$\begin{eqnarray*} \psi'(z)=\frac 1z+\frac 1{2z^2}+4z\int_0^{\infty}\frac{x}{(z^2+x^2)^2(e^{2\pi x}-1)}\,dx \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \int_0^{\infty}\frac{x}{(z^2+x^2)^2(e^{2\pi x}-1)}\,dx=\frac 1{4z}\left(\psi'(z)-\frac 1z-\frac 1{2z^2}\right) \end{eqnarray*}$$
これを用いて,
$$\begin{eqnarray*} \int_0^{\infty}\frac{x}{(1+x^2)^2\tanh\frac{\pi x}{2}}\,dx&=&\int_0^{\infty}\frac{x}{(1+x^2)^2}\,dx+2\int_0^{\infty}\frac{x}{(1+x^2)^2(e^{\pi x}-1)}\,dx\\ &=&\left[-\frac{1}{2(1+x^2)}\right]_0^{\infty}+\frac 12\int_0^{\infty}\frac{x}{\left(\left(\frac 12\right)^2+x^2\right)^2(e^{2\pi x}-1)}\,dx\\ &=&\frac 12+\frac 14\psi'\left(\frac 12\right)-1\\ &=&\frac{\pi^2}{8}-\frac 12 \end{eqnarray*}$$

$\frac{f(x)}{x}$は偶関数だから,
$$\begin{eqnarray*} \int_0^{\infty}\frac{f(x)}{x}\,dx&=&\frac 12\int_{-\infty}^{\infty}\frac{f(x)}{x}\,dx\\ &=&\frac 12\sum_{n\in\mathbb{Z}}\int_{nT}^{(n+1)T}\frac{f(x)}{x}\,dx\\ &=&\frac 12\sum_{n\in\mathbb{Z}}\int_0^T\frac{f(x)}{x+nT}\,dx\\ &=&\frac 14\sum_{n\in\mathbb{Z}}\int_0^Tf(x)\left(\frac{1}{x-nT}+\frac{1}{x+nT}\right)\,dx \end{eqnarray*}$$
ここで, $\pi\cot\pi z$の部分分数展開,
$$\begin{eqnarray*} \pi\cot\pi z&=&\frac 12\sum_{n\in\mathbb{Z}}\left(\frac 1{z-n}+\frac 1{z+n}\right) \end{eqnarray*}$$
を用いると,
$$\begin{eqnarray*} &&\frac 14\sum_{n\in\mathbb{Z}}\int_0^Tf(x)\left(\frac{1}{x-nT}+\frac{1}{x+nT}\right)\,dx\\ &=&\frac {\pi}{2T}\int_0^Tf(x)\cot\frac{\pi x}{T}\,dx\\ &=&\frac{\pi}{2T}\left(\int_0^{T/2}f(x)\cot\frac{\pi x}{T}\,dx+\int_0^{T/2}f(T-x)\cot\frac{\pi(T-x)}{T}\,dx\right)\\ &=&\frac{\pi}{T}\int_0^{T/2}f(x)\cot\frac{\pi x}{T}\,dx \end{eqnarray*}$$
となって, 示すことができました.

$0\lt a$としておきます. $t=\tan x$と置換して,
$$\begin{eqnarray*} \int_0^{\pi/4}\frac{\tan^a x-2\sin^2x}{\sin 2x\ln\tan x}\,dx&=&\int_0^1\frac{t^a-2\frac{t^2}{1+t^2}}{\frac{2t}{1+t^2}\ln t}\frac{dt}{1+t^2}\\ &=&\frac 12\int_0^1\left(\frac{t^{a-1}}{\ln t}-\frac{2t}{(1+t^2)\ln t}\right)\,dt\\ &=&\frac 12\int_0^1\frac{t^{a-1}-1}{\ln t}\,dt+\frac 12\int_0^1\left(\frac 1{\ln t}-\frac{2t}{(1+t^2)\ln t}\right)\,dt \end{eqnarray*}$$
初項はFrullani integral
$$\begin{eqnarray*} \int_0^{\infty}\frac{f(ax)-f(bx)}{x}\,dx=(f(\infty)-f(0))\ln\frac ab \end{eqnarray*}$$
より,
$$\begin{eqnarray*} \frac 12\int_0^1\frac{t^{a-1}-1}{\ln t}\,dt&=&-\frac 12\int_0^{\infty}\frac{e^{-ax}-e^{-x}}{x}\,dx\\ &=&\frac 12\ln a \end{eqnarray*}$$
第2項は
$$\begin{eqnarray*} \frac 12\int_0^1\left(\frac 1{\ln t}-\frac{2t}{(1+t^2)\ln t}\right)\,dt=-\frac 12\int_0^{\infty}\left(\frac{e^{-x}}{x}-\frac{2e^{-2x}}{x(1+e^{-2x})}\right)\,dx \end{eqnarray*}$$
ここで, Mellin変換,
$$\begin{eqnarray*} &&\int_0^{\infty}x^{s-1}\left(e^{-x}-\frac{2e^{-2x}}{1+e^{-2x}}\right)\,dx\\ &=&\Gamma(s)-2\int_0^{\infty}\frac{x^{s-1}e^{-2x}}{1+e^{-2x}}\,dx\\ &=&\Gamma(s)-2^{1-s}\int_0^{\infty}\frac{x^{s-1}}{e^x+1}\,dx\\ &=&\Gamma(s)(1-2^{1-s}\eta(s)) \end{eqnarray*}$$
において, $s\to 0$とすることで, $\eta(0)=\frac 12, \eta'(0)=\ln\frac{\pi}{2}$を用いて,
$$\begin{eqnarray*} \int_0^{\infty}\left(\frac{e^{-x}}{x}-\frac{2e^{-2x}}{x(1+e^{-2x})}\right)\,dx&=&\lim_{s\to 0}\Gamma(s)(1-2^{1-s}\eta(s))\\ &=&-\lim_{s\to 0}2^{1-s}\eta(s)\left(-\ln 2+\frac{\eta'(s)}{\eta(s)}\right)\\ &=&\ln 2-\ln\frac{\pi}{2} \end{eqnarray*}$$
よって, 求める積分は
$$\begin{eqnarray*} \frac 12\left(\ln a - \ln 2 +\ln\frac{\pi}2\right)&=&\frac 12\left(\ln \frac a2 +\ln\frac{\pi}2\right)\\ \end{eqnarray*}$$
となり, $a=2e$とすればよい.