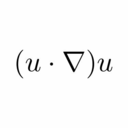どちゃ楽数学botの問題を解く Q.115

はじめに

最近数学をやってないな～と思ったので勝手ながら どちゃ楽数学bot さんの問題を解説したいと思います。

問題

解答

(1)条件(a)から$1\leq f(0)$がわかり, また(b)から
\begin{eqnarray*} f(0)f(h)&\leq& f(0+h) \\ &=&f(h) \end{eqnarray*}
であって, (a)から$h>-1$であれば$f(h)\neq 0$であるので$f(0)\leq1$がわかり, これらより$f(0)=0$となります.
次に
\begin{align*} f(x+h)-f(x)&\leq f(x)f(h)-f(x) \\ &=f(x)\{f(h)-1\} \\ &\leq f(x)h \end{align*}
が成り立ち, $h$の正負について場合分けをすれば
$$ \frac{f(x+h)-f(x)}{h}\leq f(x) \ \ \ (h>0)\\ \frac{f(x+h)-f(x)}{h}\geq f(x) \ \ \ (h<0) $$
がわかるので, $h\to 0$とすることで
$$ f(x)=f'(x) $$
を得ます. よって$f'(0)=f(0)=1$となります.

(2)先ほど得られた等式
$$ f(x)=f'(x) $$
と初期条件$f(0)=1$から$f(x)=e^x$

まとめ

正直解くのにものすごく苦労しました。でも割ときれいに解けた気もするのでﾖｼ!