直線通過条件と連分数

導入

ここでは次のような問題を扱う。

問1.次の図において、原点を通り、一つに繋がっている黄色い正方形の内部をすべて通るような直線は存在するか。

Q1Question
今回の場合は、Yesである。下の図のような直線が引けるのだ。
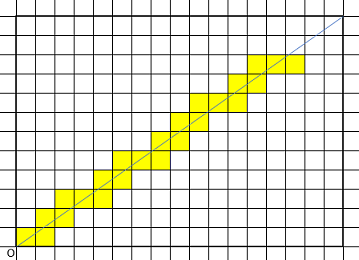Q2Answer
しかし、次のような場合はNoである。

問2.次の図において、原点を通り、黄色い正方形の内部をすべて通るような直線は存在するか

Q2
証明をしようとすると少し手間が必要なのだが、その手続きをより統一化していくと、連分数にまでつながる考え方となる。今回はそれについてを述べていく。

問題の解決方法

簡略化法

この問題において重要なのは、直線の傾き$\alpha$である。
問題を満たすような直線が$y= \alpha x$とあらわされていたとする。そして$x,y$軸を反転させることによって、$\alpha > 1$としてもよい。このとき、$y$軸方向に見たときのに、各列の直線が通る正方形の個数を考える(例えば図の$\alpha = \frac{17}{12}$では$2,2,3,2,3, \dots$)。
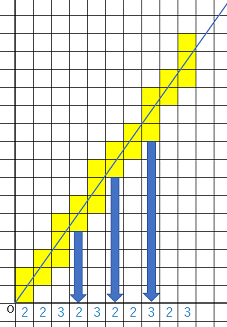a_nExplain
直線の通る$n \leq x \leq n+1$内の正方形の個数$a_n$は、次のようにあらわされる。
$$ a_n = \lceil \alpha (n+1) \rceil - \lfloor \alpha n \rfloor $$
ここで$\alpha_0 := \lfloor \alpha \rfloor$として、式変形をしてみると、
$$ \begin{eqnarray} a_n &=& \lceil \alpha (n+1) \rceil - \lfloor \alpha n \rfloor \\ &=& \lceil (\alpha-\alpha_0) (n+1) \rceil - \lfloor (\alpha-\alpha_0) n \rfloor + \alpha_0 \end{eqnarray} $$
となり、$0 \leq \alpha-\alpha_0 < 1$が成り立っている。
　ここで$a_n$と同様に、$y=(\alpha-\alpha_0)x$に対応する数列を$b_n$とすれば、
$$ a_n = b_n+\alpha_0 $$
となっている。
　何が起こっているのか、図で確認してみよう。
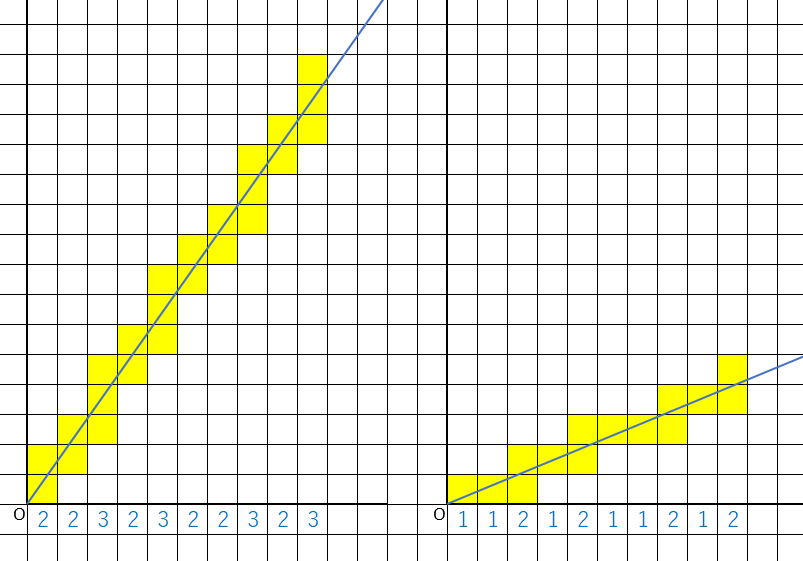anbn
左図の$y = \frac{17}{12} x$が($\alpha-\alpha_0 = \frac{5}{12}$より)右図の$y=\frac{5}{12} x$に対応してたといえる。このときに直線の通る正方形の個数は左図で$a_n$と右図で$b_n$であるが、$a_n = b_n +1$が成立しているとわかる。つまり、一般的に言えば、傾きを整数だけ変化させることによって通る正方形も一様に変化するのだ。
　ここで重要な事実が分かった。黄色の正方形を先ほどのように数列$\{ a_n \}$で表す(全ての黄色い正方形が一つに繋がっている点に注意)。そしてこの黄色い正方形を正方形列$\{ a_n \}$と呼ぶ。このとき次の補題が成立するのだ。

補題の対偶をとると、面白いことがわかるだろう。つまり、正方形列$\{ a_n \}$に対して、正方形列$\{ a_n - k\}$を通る直線が存在しないことを示せば、正方形列$\{ a_n \}$を通る直線が存在しないことが示されるのだ。言い換えれば、正方形列$\{ a_n \}$を簡略化して問題を解くことができる。

簡略化法の応用

　補題1を用いて、問2を解決してみよう。まず正方形列$\{ a_n \}_{n=0}^{p-1}$を求めると($p$は正方形列の列数)
$$ 1,2,1,2,2,1,2,1,2,1,2,2,1,2,2,1,2,1,2,1,2,2,1,2,1 $$
となる。これでは簡略化できないので、$x,y$軸を入れ替える。この時の操作は、正方形列の見る方向を$y$軸平行$\to x$軸平行にすればよいだけである。すると
$$ 2,3,2,3,3,3,2,3,2,3,3,3,2,3,2 $$
となる。ここで補題1を用いて、
$$ 1,2,1,2,2,2,1,2,1,2,2,2,1,2,1 $$
と簡略化できる。ここでまた$x,y$軸を入れ替える。すると
$$ 2,3,2,2,3,3,2,2,3,2 $$
となる補題1より
$$ 1,2,1,1,2,2,1,1,2,1 $$
$x,y$軸を入れ替えて
$$ 2,4,2,4,2 $$
補題1より
$$ 1,3,1,3,1 $$
この正方形列を通る直線は存在しない。
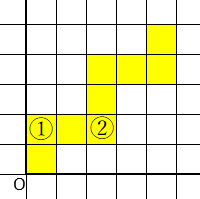Q2Simple
この証明は非常に簡潔である。

　この手順をまとめてみよう

1. $x,y$軸を入れ替えることによって、$\displaystyle \min_{m} a_m \geq 2$とする。
2. $\{ a_n \}$を$\left\{ a_n - \left( \displaystyle \min_{m} a_m - 1 \right) \right\}$と簡略化する
3. 1,2を繰り返し、1.において軸入れ替え後も$\displaystyle \min_{m} a_m \leq 1$となるまで続ける。
4. 証明をする

　ただし、4.で直線が存在した場合に、補題1より、元の正方形列に対しても直線が存在するとわかる(つまり直線の存在が二つの正方形列で同値)。そのため、この操作は直線が存在することと、存在しないこと両方の証明に用いることができるのだ。実際に問1でもやってみよう(先ほどの手順を少し改善できる)。
　問1の正方形列は
$$ 1,2,2,1,2,2,1,2,2,2,1,2,2,1,1 $$
手順1より
$$ 2,2,3,2,3,2,2,3,2,3 $$
手順2より
$$ 1,1,2,1,2,1,1,2,1,2 $$
手順1より
$$ 3,3,4,3,1 $$
ここで問題が生じる。$x,y$軸を入れ替えても$\displaystyle \min_{m} a_m \leq 1$となってしまうのだ。しかもここで直線の存在を考えるのはまだ面倒である(というよりも、この行き詰まりが長い数列で起こりえるため、対策を考える必要がある)。
　ここである技術をご紹介しよう。正方形列の最終項に新たな正方形を加えて、直線の通るべき正方形を増やすという方法だ。この新しい正方形列を通る直線が存在するならば、当然ながら元の正方形列も通っている。従って、追加された正方形列に対して直線が存在することは、元の正方形列に対して直線が存在することの十分条件なのである。ここで気になるのは逆の成立だが、こちらも条件を課せば成立していることが補題2により保証される

　これを使ってみる。行き詰っていたのは
$$ 3,3,4,3,1 $$
であった。補題2を利用すれば、直線の存在が同値な正方形列は
$$ 3,3,4,3,3 $$
となり、$\displaystyle \min_{m} a_m \geq 2$を満たすために、手順2を進めることができる。
$$ 1,1,2,1,1 $$
手順1と2を交互に進めていけば
$$ \begin{eqnarray} &&1,1,2,1,1 \\ &\mapsto&3,3 \\ &\mapsto&1,1 \\ &\mapsto&2 \\ &\mapsto&1 \\ \end{eqnarray} $$
が得られる。$1$のみの数列、つまり一つの正方形を、当然直線は通過できる。よって問1は肯定的に解決される。

連分数と格子

直線の求め方

　問1が肯定的に解決されたところで、ある疑問が残る。すなわち、どのような直線が問1を満たすのかということだ。
　ここで補題1を思い出していただきたい。補題の核となる事実は
$$ \begin{eqnarray} a_n &=& \lceil \alpha (n+1) \rceil - \lfloor \alpha n \rfloor \\ &=& \lceil (\alpha-k) (n+1) \rceil - \lfloor (\alpha-k) n \rfloor + k \end{eqnarray} $$
という部分である。ここで手順1で行ったことは、$\{a_n \}$を$\{ a_n-k \}$に置き換えたことだ。言い換えれば、$y = \alpha x$が正方形列$\{a_n \}$を通ることと、$y = (\alpha -k)x$が正方形列$\{ a_n-k \}$を通ることが同値ということだ。
　手順1においては、$x,y$軸を入れ替えている。正方形列$\{a_n \}$の$x,y$軸を入れ替えたときの正方形列を$\{ b_n \}$とすると、$y = \alpha x$が正方形列$\{a_n \}$を通ることと、$y = \frac{1}{\alpha}x$が正方形列$\{ b_n \}$を通ることが同値である。なお、補題2では証明からわかる通り、直線は変化しないことに注意する。
　これらのことを踏まえて、問1の直線(すでに書いているが$y=\frac{12}{17} x$が一つの解である)を求めてみよう。問1で用いた変形をまとめると
$$ \begin{eqnarray} && 1,2,2,1,2,2,1,2,2,2,1,2,2,1,1 &\mapsto& 2,2,3,2,3,2,2,3,2,3 \\ &\mapsto& 1,1,2,1,2,1,1,2,1,2 &\mapsto& 3,3,4,3,1(3,3,4,3,3) \\ &\mapsto& 1,1,2,1,1 &\mapsto& 3,3 \\ &\mapsto& 1,1 &\mapsto& 2 \\ &\mapsto& 1 \end{eqnarray} $$
となる。正方形列$1$を通る直線$y=\alpha _0 x$から初めて、各行の最初の正方形列を通る直線を考えてみる。ただし、左の$\mapsto$は$\alpha +k$を、右の$\mapsto$は$\frac{1}{\alpha}$を行う。左の正方形列に対する直線の傾きを下から順に$(\alpha _0,)\alpha _1,\alpha _2,\alpha _3, \alpha _4$とすれば
$$ \begin{eqnarray} \alpha_1 &=& \frac{1}{1+\alpha _0} \\ \alpha_2 &=& \frac{1}{2+\alpha _1} \\ \alpha_3 &=& \frac{1}{2+\alpha _2} \\ \alpha_4 &=& \frac{1}{1+\alpha _3} &=& \frac{1}{ 1+\frac{1}{ 2+\frac{1}{ 2+\frac{1}{ 1+\alpha _0 } } } } \end{eqnarray} $$
となる。ここで$0 < \alpha_0 < \infty$と考えて、$\alpha_4$の値域は
$$ \frac{7}{10} < \alpha _4 < \frac{5}{7} $$
と求められた。

連分数

$\alpha _0$の計算に連分数が出現した。この連分数の出現はかなり面白いことを示唆している。例えば傾きが不明で原点を通る直線と格子を渡された際に、その傾きの値の連分数を近似できるのだ(勿論大抵は実用的ではない。そのため問には取り上げなかった)。この方法によって、連分数を直感的にとらえることができればな～と思う。