オイラー・ラグランジュ方程式の表記
概要
物理学にはラグランジュの運動方程式があり、重要な方程式である一方で、微分と積分が入り混じって複雑な形をしている。ここでは表記に着目し、最速降下曲線の定式からオイラー・ラグランジュの運動方程式を導き、幾つかの一般化を含めた式の表記について考察する。
最速降下曲線問題
むかしむかし、ヨーロッパの数学者の間では問題を投げ合うのが流行っていた。そんな中、 最速降下曲線 [wikipedia] と呼ばれる問題があった。
質点が点$ a $を静止状態から一定の重力のみで加速して、沿って一番早く点$ b $に辿り着ける曲線を求めよ。
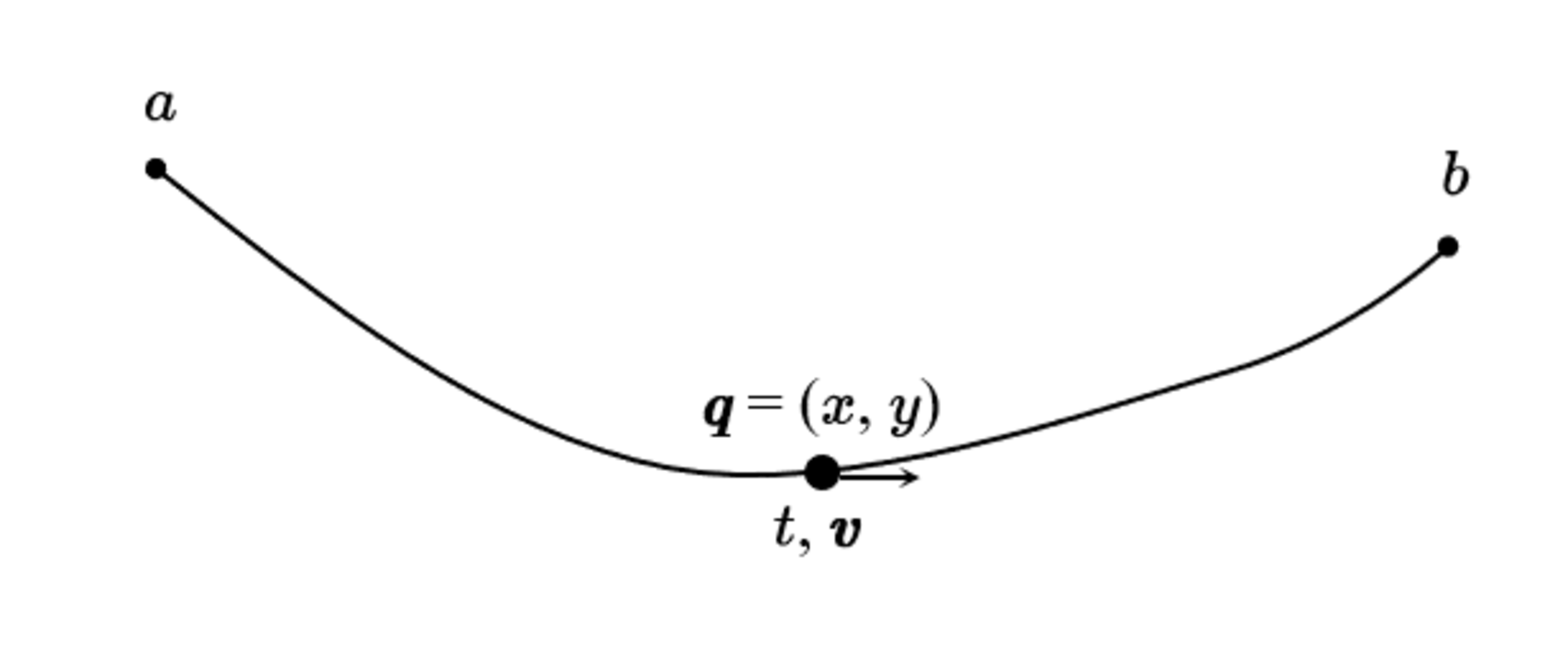 最速降下曲線問題
最速降下曲線問題
点$ a $から点$ b $までの移動時間$ T $は、質点が2点それぞれに居る時刻$ t_a $から$ t_b $までの時刻$ t $の積分として、とりあえず形式的に$ \ds T = \ind{t_a}{t_b} dt $と書ける。時刻が未知であり、求めたいのは曲線の形であるため、$ dt $を$ dx $に変えて$ x $と$ y $の関係式に変形したい。
ここで、速度$ \bec{v} $を導入すれば、その$ x $成分$ v_x = \ffd{dx}{dt} $で$ dt $を置換できる。また、力学的エネルギ保存則$ mgy = \ffd12m\bec{v}^2 $を使えば$ v_x $を消せる。$ \bec{v}^2 = 2gy $で、重力加速度$ g $は定数として残して良い。$ y $は曲線の形状情報のため残して良い。
$ \bec{v}^2 = v_x^2 + v_y^2 $であるゆえ、先に$ v_y $を$ v_x $で表してから纏めて消す。質点が曲線に沿って移動するため、速度は曲線の勾配方向に向き、$ \ffd{v_y}{v_x} = \ddd{y}{x} = y' $が成り立つので、これを使えば良い。新たに出てきた$ y' $は曲線を記述する$ x $と$ y $の関係式であるため残して良い。
以上を纏めると、$ \bec{v}^2 = v_x^2 + v_y^2 = v_x^2 \left(1 + y'^{\,2} \right) $ であるため、$ \ffd1{v_x} = \sqrt{\ffd{1 + y'^{\,2}\strut}{\bec{v}^2}} = \sqrt{\ffd{1 + y'^{\,2}\strut}{2gy}} $となる。よって、$ T = \ind{t_a}{t_b} dt = \ind{x_a}{x_b}\;\ffd{dx}{v_x} = \ind{x_a}{x_b} \!\sqrt{\ffd{1 + y'^{\,2}}{2gy}} dx $となる。後は最小の$ T $を与える関数$ y(x) $を数学的に解けば良い。
変分法
$ T = \ind{x_a}{x_b} \sqrt{\ffd{1 + y'^{\,2}}{2gy}} dx $を一般化すると、未知関数$ y $とその微分$ y' $を独立変数とする記述関数$ F(y, y') $があり、その定積分で定義される汎関数$ T(y) = \ind{x_a}{x_b} F\big(y(x),y'(x)\big) \;dx $の関数値を最小にする関数$ y $を求める問題に帰着する。
変分の原理では、関数$ y(x) $に微小な変化$ \delta y(x) $を与え、その差異によって引き起こす汎関数値の変化$ \delta T(y) $を調べる。$ \delta y(x) $は基本的に任意だが、2点$ a,b $を必ず通るため、境界条件として$ \delta y(x_a) = \delta y(x_b) = 0 $の制約を課す必要がある。
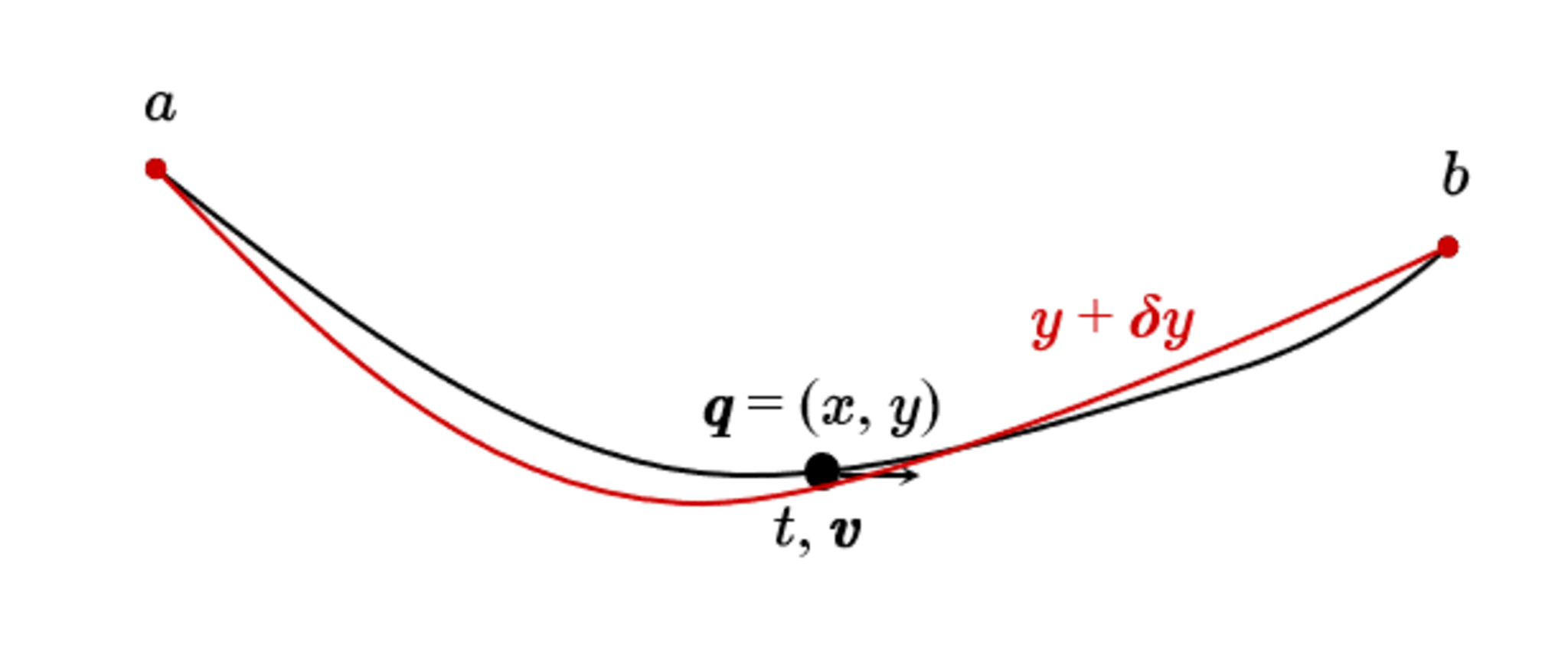 変分法
変分法
問題を簡単にするため、$ \delta y $を微小な定数値$ \ge $と任意の関数$ \gh(x) $の積に分けて定義する:$ \delta y = \ge\,\gh(x) $。また、境界条件を$ \gh(x_a) = \gh(x_b) = 0 $の形で引き継ぐ。すると、如何なる$ \delta y $を加えても$ T(y) $が最小値を取るとき、少なくとも$ \ddd{T(y+\ge\,\gh)}{\ge} = 0 $が成り立っている必要がある。これは代入してから$ \ge $で微分する意味である。
更に記号法として、$ u = y + \delta y = y + \ge\,\gh $を定義して置く。すなわち、$ u(x) = y(x) + \ge\,\gh(x) $、$ u'(x) = y'(x) + \ge\,\gh'(x) $。これで解くべき問題は$ \ddd{T(u)}{\ge} = \ddd{}{\ge}\ind{x_a}{x_b} F\big(u(x),u'(x)\big) \;dx = 0 $になる。
ここからは一気に計算する。微分と積分が交換可能であり、連鎖則に従い、部分積分もできる。部分積分で、$ \left[ \ppd{F\big(u(x),u'(x)\big)}{u(x)} \gh(x) \right]_{x_a}^{x_b} $が出てくるが、境界条件$ \gh(x_a) = \gh(x_b) = 0 $が効いているため、$ 0 $に消える。
$$
\ddd{T(u)}{\ge} = \ddd{}{\ge} \ind{x_a}{x_b} F\big(u(x),u'(x)\big) dx\\
\phantom{\ppd{T(u)}{\ge}} = \ind{x_a}{x_b} \ddd{}{\ge} F\big(u(x),u'(x)\big) dx\\
\phantom{\ppd{T(u)}{\ge}} = \ind{x_a}{x_b} \left(
\ppd{F\big(u(x),u'(x)\big)}{u(x)} \ddd{u(x)}{\ge}
+ \ppd{F\big(u(x),u'(x)\big)}{u(x)} \ddd{u'(x)}{\ge} \right) dx\\
\phantom{\ppd{T(u)}{\ge}} = \ind{x_a}{x_b} \left(
\ppd{F\big(u(x),u'(x)\big)}{u(x)} \gh(x)
+ \ppd{F\big(u(x),u'(x)\big)}{u(x)} \gh'(x) \right) dx\\
\phantom{\ppd{T(u)}{\ge}} = \ind{x_a}{x_b} \left(
\ppd{F\big(u(x),u'(x)\big)}{u(x)} \gh(x)
- \left[ \ddd{}{x}\ppd{F\big(u(x),u'(x)\big)}{u'(x)} \right] \gh(x) \right) dx
+ \left[ \ppd{F\big(u(x),u'(x)\big)}{u(x)} \gh(x) \right]_{x_a}^{x_b}\\
\phantom{\ppd{T(u)}{\ge}} = \ind{x_a}{x_b} \left(
\ppd{F\big(u(x),u'(x)\big)}{u(x)}
- \ddd{}{x} \ppd{F\big(u(x),u'(x)\big)}{u'(x)} \right) \gh(x) \;dx\\
$$
これが任意の$ \gh(x) $に対し常に$ 0 $であるためには、積分対象を$ 0 $にするしかない。これがオイラー・ラグランジュ方程式になる。
$$
\ppd{F\big(u(x),u'(x)\big)}{u(x)}
- \ddd{}{x} \ppd{F\big(u(x),u'(x)\big)}{u'(x)} = 0
$$
微分と代入の読み方
導出の過程から、オイラー・ラグランジュ方程式に含まれる偏微分は「先に変微分してから代入する」のに対し、常微分は「先に代入してから微分する」。良く用いられる微分の表記では、この代入と微分の順番は曖昧になっているため、注意が必要である。
一般に、合成関数の微分では、微分する対象で代入と微分の順番が決まる。例えば合成関数$ f(g(x)) $の微分は$ \ddd{f}{x} = \ddd{f}{g} \ddd{g}{x} $と表記される。$ \ddd{f}{x} $は代入する関数$ g(x) $の独立変数$ x $で微分するように表記し、$ f $に$ g(x) $を代入してからの微分を意味する。対し、$ \ddd{f}{g} $は代入する関数$ g $で微分するように表記し、$ g(x) $を先に微分してからの代入を意味する。
すると、オイラー・ラグランジュ方程式に含まれる$ \ddd{}{x} \ppd{F\big(u(x),u'(x)\big)}{u'(x)} $の意味は、偏微分が代入する関数$ u'(x) $で微分するため代入してからの微分で、常微分は代入する関数$ u(x) $や$ u'(x) $の独立変数で微分するため微分してからの代入と読める。
代入前後の定義域の問題
合成関数$ F\big(u(x),u'(x)\big) $では、$ u'(x) $が$ u(x) $の微分で互いに独立してないため、定義域に関して混乱し易い。具体に、$ F(m,n) $と定義すれば2次元空間が定義域とも成り得るが、$ F\big(u(x),u'(x)\big) $と代入すれば定義域が1次元に限定される。物理的に見れば、問題が1次元の$ x $軸上でしか定義されないため、$ F(m,n) $を偏微分するための2次元空間の殆どが「定義域外」と錯覚し易い。
これに対し、$ F $の定義域$ D $が物理的に意味のある領域$ U = \left\{\big(u(x),u'(x)\big)\right\} $を含む関係にあり、代入前は$ D $、代入で$ U $に制限されると考えると良い。すなわち、関数$ F $の解析は広い2次元空間で行い、解析した結果を物理的に意味のある1次元空間に限定して使えば辻褄が合う算段である。
多次元への一般化
未知関数$ u $がベクトル関数の場合、縮約記法では$ u_i $と表記する。記述関数$ F $は全ての要素の関数になる。
$$
F\big(u_0(x), \dots, u_i(x),\dots,u_I(x), u_0'(x),\dots, u_i'(x),\dots,u_I'(x)\big)
$$
ベクトル表記で$ F\big(\bec{u}(x), \bec{u}'(x)\big) $と書くように、縮約記法では縮約せずに$ F\big(u(x), u'(x)\big) $と書く。$ F\big(u_i(x), u_i'(x)\big) $とも書けるが、縮約記法では添字の数で総和を取る対象を判断するため、関数の代入値に添字が含まれると紛らわしくなる。例えば、2次元で$ \ddd{f(x_i)}{x_i} $と書いても$ \ddd{f(x_i)}{x_i} = \left( \ddd{f(x_0, x_1)}{x_0}, \ddd{f(x_0,x_1)}{x_1} \right) $というベクトル値あって、$ \ddd{f(x_0)}{x_0} + \ddd{f(x_1)}{x_1} $というスカラー値には成らない。関数の括弧の中は外と無関係と分かれば、$ \ddd{f(x_i)}{x_i} $でも良い。無関係と主張して$ \ddd{f(x_\mu)}{x_i} $と書いても良いが、対応が崩れるのと、添字に使える文字を消費してしまう弱点がある。
結果的に、オイラー・ラグランジュ方程式は単純な書き換えで済む。
$$
\ppd{F\big(u(x),u'(x)\big)}{u_i(x)}
- \ddd{}{x} \ppd{F\big(u(x),u'(x)\big)}{u_i'(x)} = 0
$$
位置$ x $もベクトル値の場合、縮約記法では反変成分で$ x^j $と書き、記述関数$ F $は全ての$ u_i $とその勾配の関数となる。勾配はベクトル勾配として$ \nabla\bec{u} = \ppd{u_i}{x^j} = \partial_j u_i = u_{i,j} $で表記され、$ u_i $と$ x^j $の全組合わせだけの成分を持つ。$ F $の引数を全て並べて書くと:
$$
F\left(
\begin{array}{c}
u_0\;\;(x^0,\cdots,x^J), \dots, u_i\;\;(x^0,\cdots,x^J),\dots,u_I\;\;(x^0,\cdots,x^J), \\
u_{0,0}(x^0,\cdots,x^J), \dots, u_{i,0}(x^0,\cdots,x^J),\dots,u_{I,0}(x^0,\cdots,x^J), \\
\vdots \\
u_{0,J}(x^0,\cdots,x^J), \dots, u_{i,J}(x^0,\cdots,x^J),\dots,u_{I,J}(x^0,\cdots,x^J), \\
\end{array}
\right)
$$
これを$ F\big( \bec{u}(x), \nabla\bec{u}(x) \big) $や$ F\big( u(x), \partial u(x) \big) $と表記される。
オイラー・ラグランジュ方程式は未知変数の偏微分項がやたらと増えて、常微分の部分も偏微分に変わって内積を取る。ベクトル記法では
$$
\ppd{F\big(\bec{u}(\bec{x}),\nabla\bec{u}(\bec{x})\big)}{\bec{u}(\bec{x})}
- \nabla\cdot\ppd{F\big(\bec{u}(\bec{x}),\nabla\bec{u}(\bec{x})\big)}{(\nabla\bec{u}(\bec{x}))} = 0
$$
縮約記法では
$$
\ppd{F\big(u(x),\partial u(x)\big)}{u_i(x)}
- \ppd{}{x^j} \ppd{F\big(u(x),\partial u(x)\big)}{u_{i,j}(x)} = 0
$$
$$
\ppd{F\big(u(x),\partial u(x)\big)}{u_i(x)}
- \ppd{}{x^j} \ppd{F\big(u(x),\partial u(x)\big)}{(\partial_j u_i(x))} = 0
$$
$$
\ppd{F\big(u_i(x_s),\partial_j u_i(x_s)\big)}{u_i(x_s)}
- \ppd{}{x^j} \ppd{F\big(u_i(x_s),\partial_j u_i(x_s)\big)}{(\partial_j u_i(x_s))} = 0
$$
