黄金比および Lucas 数, Fibonacci 数の定義と再帰性

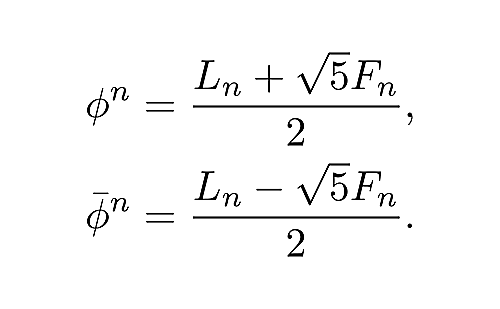黄金比の累乗
前提知識 : 漸化式, 数学的帰納法
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

黄金比

黄金比
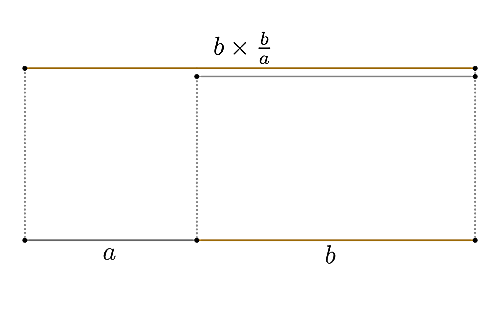
上の図の示すように, 正なる数$a,b$によって表された比率$a:b$が比例式
$$ \begin{align} a:b=b:(a+b) \end{align} $$すなわち
$$ \begin{align} \left(\frac{b}{a}\right)^2=\frac{b}{a}+1 \end{align} $$を満足するとき, これを黄金比 (golden ratio, aurea ratio) あるいは中末比, 外中比と言って, 比の値$a/b$もまた黄金比と言う.

黄金比は, 下の図のように正五角形 (正五芒星) の至る箇所にて線分長の比率として現れることが知られている. これは, 正五角形の対角線がそれぞれの内角を三等分し, 三角形の相似関係から$a:b=b:(a+b)$なる線分長の関係式が導かれることに由るものである.
正五角形

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

Lucas 数列と Fibonacci 数列

黄金比$\phi$の累乗は, 有理数$a,b$を用いた$\dfrac{a+\sqrt{5}b}{2}$の式形に表せば, 順に
$$ \begin{align} \phi^0&=\frac{2+0\sqrt{5}}{2}\ (=1),\\\\ \phi^1&=\frac{1+1\sqrt{5}}{2}\ \left(=\frac{1+\sqrt{5}}{2}\right),\\\\ \phi^2&=\frac{3+1\sqrt{5}}{2}\ \left(=\frac{3+\sqrt{5}}{2}\right),\\\\ \phi^3&=\frac{4+2\sqrt{5}}{2}\ (=2+\sqrt{5}),\\\\ \phi^4&=\frac{7+3\sqrt{5}}{2},\\\\ \phi^5&=\frac{11+5\sqrt{5}}{2},\\\\ \phi^6&=\frac{18+8\sqrt{5}}{2}\ (=9+4\sqrt{5}),\\\\ \phi^7&=\frac{29+13\sqrt{5}}{2},\\\\ \phi^8&=\frac{47+21\sqrt{5}}{2},\\\\ \phi^9&=\frac{76+34\sqrt{5}}{2}\ (=38+17\sqrt{5}),\\\\ \phi^{10}&=\frac{123+55\sqrt{5}}{2},\\\\ \phi^{11}&=\frac{199+89\sqrt{5}}{2},\\\\ \phi^{12}&=\frac{322+144\sqrt{5}}{2}\ (=161+72\sqrt{5}),\\\\ &\ \ \vdots \end{align} $$のように計算される. $\sqrt{5}$の無理数性に留意して, 任意の$n\in\mathbb{Z}_{\geqslant0}$について
$$ \begin{align} \phi^n=\frac{a\_n+\sqrt{5}b\_n}{2} \end{align} $$なる有理数列$(a_n)_{n\geqslant0},(b_n)_{n\geqslant0}$を定めれば, 恒等式$\phi^{n+2}=\phi^{n+1}+\phi^n$の成立のため
$$ \begin{align} \begin{cases} a_{n+2}=a_{n+1}+a_n\\\\ b_{n+2}=b_{n+1}+b_n \end{cases} \end{align} $$を得, 再帰的に, $a_n,b_n$はいずれも整数値のみを取りうることが判る. これらの数列$(a_n),(b_n)$を, 十九世紀フランスの数学者 François Édouard Anatole Lucas および十二世紀, 十三世紀イタリアの数学者 Leonardo Fibonacci (Leonardo Pisano) に因んで, それぞれ Lucas (の) 数列, Fibonacci (の) 数列と言い, 記号では$(L_n),(F_n)$と書きあらわす.

このような導入は数列$(L_n),(F_n)$の満足する漸化式のみならず初期値の必然性をも理解するにあたり極めて自然で重要なるものであるが, 現実このような定義による認識はあまり広くに及んでいないように思われる. 遺憾ではあるが, ここでは線型回帰数列としての$(L_n),(F_n)$の性質に定義を明けわたし, 上記をそこから証明される定理と見なす.

先にも見たように, 各数列は
$$ \begin{align} &(L_n)_{n\geqslant0}=2,1,3,4,7,11,18,29,47,76,123,199,322,\ldots,\\ &(F_n)_{n\geqslant0}=0,1,1,2,3,5,8,13,21,34,55,89,144,\ldots \end{align} $$のように始まる.

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$

負数インデックス

Lucas 数列や Fibonacci 数列が$n\geqslant0$において満たしていた諸性質を崩すこと無く$\mathbb{Z}$の全域にまでインデックスを拡張するには, それらにとって充分であるような条件, すなわち定義を引きつげばよろしい. そこで, 次のように Lucas 数列および Fibonacci 数列をいま一度定義する.

これに従えば, $n\in\{-1,-2,-3,-4,-5\}$のときは
$$ \begin{align} &L_{-1}=L_1-L_0=-1,\\\\ &L_{-2}=L_0=L_{-1}=3,\\\\ &L_{-3}=L_{-1}-L_{-2}=-4,\\\\ &L_{-4}=L_{-2}-L_{-3}=7,\\\\ &L_{-5}=L_{-3}-L_{-4}=-11,\\\\ &\ \\\\ &F_{-1}=F_1-F_0=1,\\\\ &F_{-2}=F_0-F_{-1}=-1,\\\\ &F_{-3}=F_{-1}-F_{-2}=2,\\\\ &F_{-4}=F_{-2}-F_{-3}=-3,\\\\ &F_{-5}=F_{-3}-F_{-4}=5 \end{align} $$と計算され, 等式$L_{-n}=(-1)^nL_n,\ $$F_{-n}=(-1)^{n+1}F_n$の成立が察せられるであろう.

インデックスの符号の反転は整数論的にも大いなる意義を有する. たとえば, あらゆる整数$n$について
\begin{align} n\equiv1\ \ ({\rm mod}\ 6)\Longrightarrow F_n\equiv1\ \ ({\rm mod}\ 4) \end{align}が成立することが判明しているとき, $n$を$-n$に置きかえることによって
\begin{align} n\equiv5\ \ ({\rm mod}\ 6)\Longrightarrow F_n\equiv1\ \ ({\rm mod}\ 4) \end{align}を直ちに示すことができる.

相互関係式を適用することによって, $L_n$あるいは$F_n$を, 次数を変えることなく$F_{n+1},F_{n-1}$あるいは$L_{n+1},L_{n-1}$の式へと書きかえることができる.

これは, $\overrightarrow{x}_n=\left(\begin{array}{c}L_n\\F_n\end{array}\right)$と置けば
\begin{align} \overrightarrow{x}_{n+1}=\left(\begin{array}{cc}1/2&5/2\\\\1/2&1/2\end{array}\right)\overrightarrow{x}_n \end{align}と表現することもでき, 各変量の持つ情報を大きくしたことによって, 一つ階数の低い二項間漸化式により表現されたと解することができる.

$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$