半角の公式の証明

まず、半角の公式とは、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \sin^2\frac{\theta}{2} = \frac{1-\cos\theta}{2} \\ \cos^2\frac{\theta}{2} = \frac{1+\cos\theta}{2} \\ \tan^2\frac{\theta}{2} = \frac{1-\cos\theta}{1+\cos\theta} \end{array} \right. \end{eqnarray} $$
という公式である。
よく倍角の公式から変形して示すことが多いが、直接示す方法でもできそうだったのでやってみた。($\tan$は$\frac{\sin}{\cos}$を計算するだけなので省略)

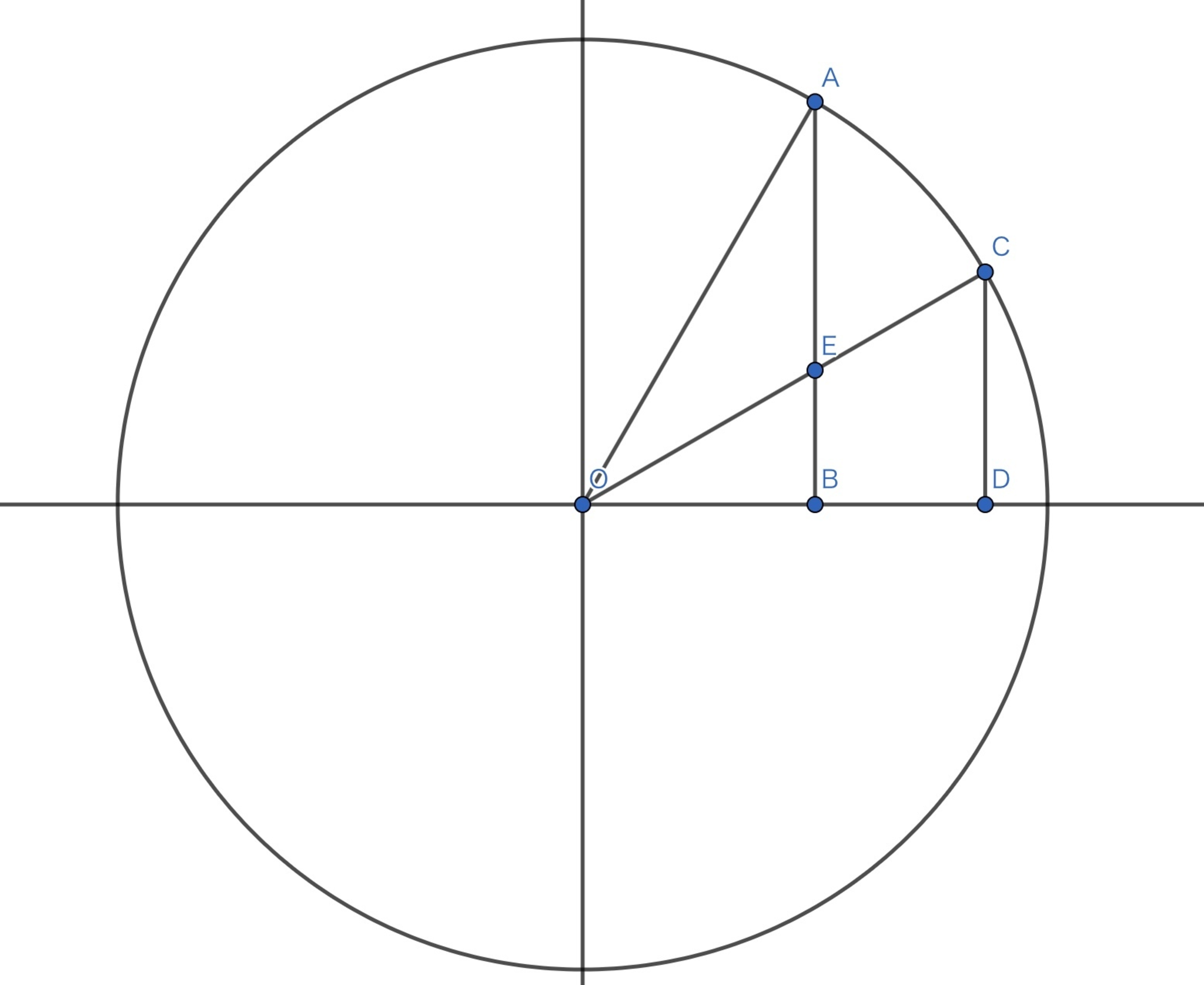
$\angle AOB=\theta(0\leq\theta\lt\frac{\pi}{2})$とおき、$OC$は$OA$と$OB$の角二等分線、円の半径は1とする。
すると、$\sin\frac{\theta}{2}=CD,\cos\frac{\theta}{2}=OC$になるのでこれらの長さが求まればよい。
まず$AB=\sin\theta,OB=\cos\theta$であり、角の二等分線定理より$AE:EB=1:\sin\theta$なので、$BE=\frac{\sin\theta\cos\theta}{1+\cos\theta}$となる。
次は$OE$の長さを求める。三平方の定理より、$OE=OB^2+EB^2$である。
よって、$OE=\sqrt{\cos^2\theta+(\frac{\sin\theta\cos\theta}{1+\cos\theta})^2}=\sqrt{cos^2\theta+\frac{(1-\cos^2\theta)\cos^2\theta}{(1+\cos\theta)^2}}=\sqrt{\frac{2\cos^2\theta+2\cos^3\theta}{(1+\cos\theta)^2}}\\=\sqrt{2}\cos\theta\sqrt{\frac{1+\cos\theta}{(1+\cos\theta)^2}}=\sqrt{2}\frac{\cos\theta}{1+\cos\theta}\sqrt{1+\cos\theta}$
そして、ついに$CD$と$OC$の長さを求められる所まで来た。
$\triangle OBE\sim\triangle OCD$より$CD=\frac{OA\cdot OD}{OE},OC=\frac{AE\cdot OD}{OE}$なので、
$CD=\frac{\sin\theta\cos\theta}{1+\cos\theta}\cdot\frac{1+\cos\theta}{\sqrt{2}\cos\theta\sqrt{1+\cos\theta}}=\sqrt{\frac{\sin^2\theta}{2(1+\cos\theta)}}=\sqrt{\frac{1-\cos^2\theta}{2(1+\cos\theta)}}=\sqrt{\frac{1-\cos\theta}{2}}$
$OC=\cos\theta\frac{1+\cos\theta}{\sqrt{2}\cos\theta\sqrt{1+\cos\theta}}=\sqrt{\frac{1+\cos\theta}{2}}$
よって、$0\leq\theta\lt\frac{\pi}{2}$の時、
$$ \begin{eqnarray} \left\{ \begin{array}{l} \sin\frac{\theta}{2}=\sqrt{\frac{1-\cos\theta}{2}} \\ \cos\frac{\theta}{2}=\sqrt{\frac{1+\cos\theta}{2}} \end{array} \right. \end{eqnarray} $$
ということが導けた。両辺を2乗すれば半角の公式になる。
$\sin(\theta+\pi)=-\sin\theta$などを使えば、$\theta$の範囲を$0\leq\theta\lt2\pi$に拡張できるだろう。