みゆ🌹の魔法 その５ 平方根の和でほぼ整数を作るよ！

夢オチ

うちのナマギリ女神さまから、整数を平方根の和（無理数）で近似できるよっていうお告げがありました。

$\cdots$っていう夢をみました。　夢か～い、チャンチャン♪♪

とはいえ、起きてから実際に試してみるとそのお告げ通りの計算結果を得られたので、今回は夢の中で授かった魔法について紹介したいと思います！

魔法の手順

１．任意の正整数 $a,~b$ からなる無理数 $\sqrt{a^2+b^2}$ を適当に有理数化します。

　$\sqrt{a^2+b^2}\fallingdotseq\frac mn$

有理数化の方法は問いませんが、高精度なほどよいです。 apu さんの記事「 自然数の平方根を任意の精度で有理数近似する方法 」あたりを参考にしてみてね(*´ω｀*)

例）$a=2,~b=1$ $\rightarrow$ $\sqrt{2^2+1^2}=\sqrt{5}\fallingdotseq\frac{559}{250}$

２．任意の整数 $k$ を用いて次のようにすれば完成！

$\sqrt{(a^2+b^2)k^2}+\sqrt{[(bn)^2-(m-an)^2-ak]^2+[2bn(m-an)-bk]^2}$

例）$k=3$ $\rightarrow$ $\begin{align}&\sqrt{45}+\sqrt{[250^2-59^2-6]^2+[2\times250\times59-3]^2}\\&\sqrt{45}+\sqrt{4352607178}\fallingdotseq~65981.00000005563\cdots\end{align}$

どーしてこれで近似されるの？

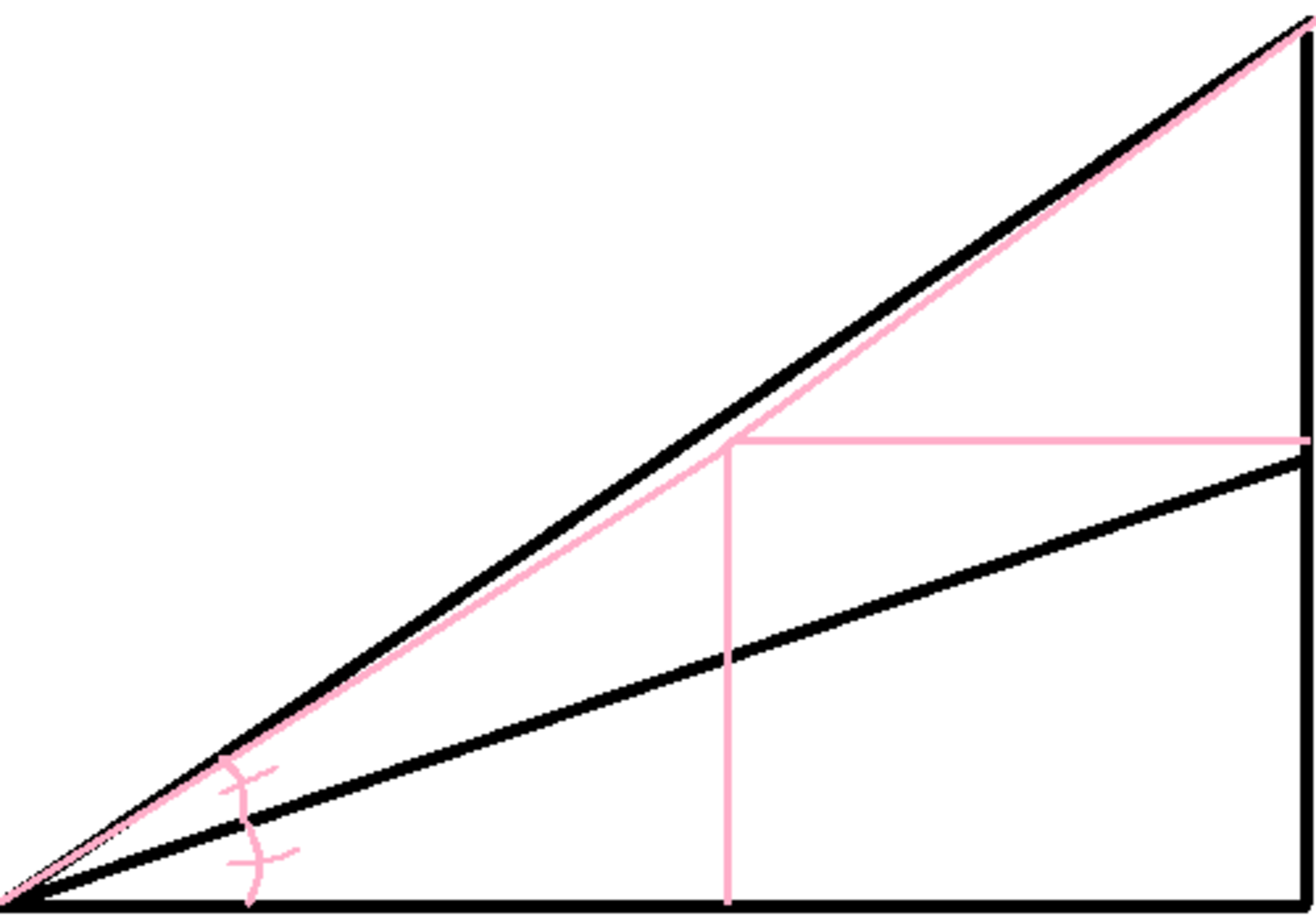夢で見た絵

いろいろ唐突でイミフかもしれませんが、夢なんてそんなものなので、とりま私が視た景色をがんばって翻訳してみます(；´∀｀)

まず、直角を挟む二辺の長さが $bn$ と $m-an$ である直角三角形の斜辺の長さを考えます。あ、$a,~b,~m,~n$ は正整数で、$\sqrt{a^2+b^2}\fallingdotseq\frac mn$ と近似される関係ってことで！

$$~\begin{align} \sqrt{(bn)^2+(m-an)^2}=&~|bn+(m-an)i|\\ =&~\left|bn+n\left(\frac mn-a\right)i\right|\\ \fallingdotseq&~|bn+n(\sqrt{a^2+b^2}-a)i| \end{align}$$
より
$$~\begin{align} ~|bn+(m-an)i|^2=&|[(bn)^2-(m-an)^2]+2bn(m-an)]i|\\ \fallingdotseq~\left|bn+n\left(\sqrt{a^2+b^2}-a\right)i\right|^2=&2n^2\left(\sqrt{a^2+b^2}-a\right)\left|a+bi\right|\\ \end{align}$$
であることがわかります。これはさきほどの直角三角形の鋭角の倍角を鋭角に持つような新たな直角三角形を想定しているわけですが、この両右辺をみると実部と虚部の比率は
$$~[(bn)^2-(m-an)^2]:[2bn(m-an)]\fallingdotseq a:b=ak:bk$$
となってますよね。そーゆー比率で近似されるということは
$$\quad\begin{align} &|bn+(m-an)i|^2\\ =&~\left(\sqrt{[(bn)^2-(m-an)^2]^2+[2bn(m-an)]^2}\right)^2\\ \fallingdotseq&~\left(\sqrt{(a^2+b^2)k^2}+\sqrt{[(bn)^2-(m-an)^2-ak]^2+[2bn(m-an)-bk]^2}\right)^2\\ \end{align}$$
というように斜辺を近似分割しても値は大きく変わらないはず。しかも
$$~[(bn)^2-(m-an)^2]^2+[2bn(m-an)]^2$$
は整数ですから、分割した斜辺も整数に近似されるよねっていうカラクリでした(*´∀｀*)