積分botを解けるだけ解く, その7

積分区間を$(-\pi,\pi)$にすると, Fourier級数の定数項だけを考えればいいから,
$$\begin{eqnarray*} &&\int_0^{\pi}\frac{dx}{(1+a^2-2a\cos x)(1+b^2-2b\cos x)}\\ &=&\frac 12\int_{-\pi}^{\pi}\frac{dx}{(1+a^2-2a\cos x)(1+b^2-2b\cos x)}\\ &=&\frac{1}{2(1-a^2)(1-b^2)}\int_{-\pi}^{\pi}\left(1+\frac{ae^{ix}}{1-ae^{ix}}+\frac{ae^{-ix}}{1-ae^{-ix}}\right)\left(1+\frac{be^{imx}}{1-be^{imx}}+\frac{be^{-imx}}{1-be^{-imx}}\right)\,dx\\ &=&\frac 1{2(1-a^2)(1-b^2)}\int_{-\pi}^{\pi}\left(1+\frac{ae^{ix}}{1-ae^{ix}}\frac{be^{-imx}}{1-be^{-imx}}+\frac{ae^{-ix}}{1-ae^{-ix}}\frac{be^{imx}}{1-be^{imx}}\right)\,dx\\ &=&\frac 1{2(1-a^2)(1-b^2)}\int_{-\pi}^{\pi}\left(1+\sum_{0\lt r,s}a^rb^se^{i(r-ms)}+\sum_{0\lt r,s}a^rb^se^{-i(r-ms)}\right)\,dx\\ &=&\frac 1{2(1-a^2)(1-b^2)}\int_{-\pi}^{\pi}\left(1+2\sum_{0\lt s}a^{ms}b^s\right)\,dx\\ &=&\frac{\pi}{(1-a^2)(1-b^2)}\frac{1+a^mb}{1-a^mb} \end{eqnarray*}$$
となって, 示すことができた.

$x\to e^{-x}$と置換して,
$$\begin{eqnarray*} \int_0^1x\li\left(\frac 1x\right)\ln^{1/4}\left(\frac 1x\right)\,dx&=&\int_0^{\infty}x^{1/4}e^{-2x}\Ei(x)\,dx\\ &=&\frac 1{2^{5/4}}\int_0^{\infty}x^{1/4}e^{-x}\Ei\left(\frac x2\right)\,dx \end{eqnarray*}$$
ここで,

$$\begin{eqnarray*} \Ei(x)=\gamma+\ln x+\sum_{0\lt n}\frac{1}{n!n}x^n \end{eqnarray*}$$
より, 項別に積分して,
$$\begin{eqnarray*} \int_0^{\infty}x^{1/4}e^{-x}\Ei\left(\frac x2\right)\,dx&=&\int_0^{\infty}x^{1/4}e^{-x}\left(\gamma+\ln \frac x2\right)\,dx+\sum_{0\lt n}\frac 1{2^nn!n}\int_0^{\infty}x^{n+1/4}e^{-x}\,dx\\ &=&\Gamma\left(\frac 54\right)\left(\gamma-\ln 2+\psi\left(\frac 54\right)\right)+\sum_{0\lt n}\frac{\Gamma\left(n+\frac 54\right)}{2^nn!n}\\ &=&\Gamma\left(\frac 54\right)\left(4-\frac{\pi}2-4\ln 2+\sum_{0\lt n}\frac{\left(\frac 54\right)_n}{2^nn!n}\right)\\ \end{eqnarray*}$$
ここで,

$$\begin{eqnarray*} \sum_{0\lt n}\frac{\left(\frac 54\right)_n}{2^nn!n}&=&\int_0^{1/2}\frac{(1-x)^{-5/4}-1}{x}\,dx\\ &=&\int_{1/2}^1\frac{x^{-5/4}-1}{1-x}\,dx\\ &=&-\gamma-\psi\left(-\frac 14\right)+\ln 2-\sum_{0\leq n}\frac{1}{2^{n-1/4}\left(n-1/4\right)}\\ &=&-4-\frac{\pi}2+4\ln 2+4\sqrt[4]{2}-4\sum_{0\leq n}\frac{1}{2^{n+3/4}(4n+3)}\\ &=&-4-\frac{\pi}2+4\ln 2+4\sqrt[4]{2}-2\tanh^{-1}\frac{1}{\sqrt[4]{2}}+2\tan^{-1}\frac{1}{\sqrt[4]{2}} \end{eqnarray*}$$
よって, これを先ほどの式に代入して,

$$\begin{eqnarray*} \int_0^{\infty}x^{1/4}e^{-x}\Ei\left(\frac x2\right)\,dx&=&\Gamma\left(\frac 54\right)\left(4\sqrt[4]{2}-\pi-2\tanh^{-1}\frac 1{\sqrt[4]{2}}+2\tan^{-1}\frac 1{\sqrt[4]{2}}\right)\\ &=&\Gamma\left(\frac 54\right)\left(4\sqrt[4]{2}-2\left(\tan^{-1}\sqrt[4]{2}+\tanh^{-1}\frac{1}{\sqrt[4]{2}}\right)\right)\\ &=&\left(\sqrt[4]{2}-\frac 12\left(\tan^{-1}\sqrt[4]{2}+\tanh^{-1}\frac{1}{\sqrt[4]{2}}\right)\right)\Gamma\left(\frac 14\right) \end{eqnarray*}$$
よって,

$$\begin{eqnarray*} \int_0^1x\li\left(\frac 1x\right)\ln^{1/4}\left(\frac 1x\right)\,dx&=&\frac{1}{2^{5/4}}\left(\sqrt[4]{2}-\frac 12\left(\tan^{-1}\sqrt[4]{2}+\tanh^{-1}\frac{1}{\sqrt[4]{2}}\right)\right)\Gamma\left(\frac 14\right)\\ &=&\left(\frac 12-\frac{\tan^{-1}\sqrt[4]{2}+\tanh^{-1}\frac 1{\sqrt[4]{2}}}{4\sqrt[4]{2}}\right)\Gamma\left(\frac 14\right) \end{eqnarray*}$$

まず,
$$\begin{eqnarray*} \int_0^1\ln\frac{1}{x^s+(1-x)^s}\frac{dx}{x}&=&-\int_0^{1/2}\ln(x^s+(1-x)^s)\left(\frac 1x+\frac 1{1-x}\right)\,dx\\ &=&-\int_0^{1/2}\frac{\ln(x^s+(1-x)^s)}{x(1-x)}\,dx \end{eqnarray*}$$
$x\to \frac{x}{1+x}$の置換により,
$$\begin{eqnarray*} -\int_0^{1/2}\frac{\ln(x^s+(1-x)^s)}{x(1-x)}\,dx&=&-\int_0^1\frac{\ln\left(\frac{1+x^s}{(1+x)^s}\right)}{x}\,dx\\ &=&-\int_0^1\frac{\ln(1+x^s)}{x}\,dx+s\int_0^1\frac{\ln(1+x)}{x}\,dx\\ &=&\left(s-\frac 1s\right)\int_0^1\frac{\ln(1+x)}{x}\,dx\\ &=&\left(s-\frac 1s\right)\sum_{0\lt n}\frac{(-1)^{n-1}}{n}\int_0^1x^{n-1}\,dx\\ &=&\left(s-\frac 1s\right)\sum_{0\lt n}\frac{(-1)^{n-1}}{n^2}\\ &=&\frac{\pi^2}{12}\left(s-\frac 1s\right) \end{eqnarray*}$$
よって, 示された.

少し前の記事( https://mathlog.info/articles/1901 ) の命題10において, $n=0$とすればよい.

項別積分により,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{e^{-ax}}{1+e^{-bx}}\,dx&=&\int_0^{\infty}\frac{e^{-ax}}{1+e^{-bx}}\,dx+\int_0^{\infty}\frac{e^{-(b-a)x}}{1+e^{-bx}}\,dx\\ &=&\int_0^{\infty}(e^{-ax}+e^{-(b-a)x})\sum_{0\leq n}e^(-1)^n{-bnx}\,dx\\ &=&\sum_{0\leq n}(-1)^n\int_0^{\infty}(e^{-(a+bn)x}+e^{-(b(n+1)-a)})\,dx\\ &=&\sum_{0\leq n}(-1)^n\left(\frac 1{a+bn}+\frac 1{b(n+1)-a}\right)\\ &=&\frac 12\sum_{n\in\mathbb{Z}}(-1)^n\left(\frac 1{a+bn}+\frac 1{a-bn}\right) \end{eqnarray*}$$
ここで, $\frac {\pi}{\sin\pi x}$の部分分数展開,
$$\begin{eqnarray*} \frac{\pi}{\sin\pi x}=\frac 12\sum_{n\in\mathbb{Z}}(-1)^n\left(\frac 1{x+n}+\frac 1{x-n}\right) \end{eqnarray*}$$
より,
$$\begin{eqnarray*} \frac 12\sum_{n\in\mathbb{Z}}(-1)^n\left(\frac 1{a+bn}+\frac 1{a-bn}\right)&=&\frac{\pi}{b\sin\frac{\pi a}{b}} \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{e^{-ax}}{1+e^{-bx}}\,dx=\frac{\pi}{b\sin\frac{\pi a}{b}} \end{eqnarray*}$$
ここに, $a=1, b=2\pi$を代入すればよい.

1つ目の命題の証明で用いた式を書き換えると,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{\cosh 2\pi ax}{\cosh\pi cx}\,dx=\frac{1}{c\cos\frac{\pi a}{c}} \end{eqnarray*}$$
また,
$$\begin{eqnarray*} \end{eqnarray*}$$
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{\cosh 2\pi ax}{\cosh\pi cx}\cosh2\pi bx\,dx&=&\frac 12\int_{-\infty}^{\infty}\frac{\cosh 2\pi(a+b)x+\cosh 2\pi(a-b)}{\cosh\pi cx}\,dx\\ &=&\frac{1}{2c}\left(\frac {1}{\cos\frac{\pi}{c}(a+b)+\cos\frac{\pi}{c}(a-b)}\right) \end{eqnarray*}$$
$b\to bi$として,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{\cosh 2\pi ax}{\cosh\pi cx}\cos2\pi bx\,dx&=&\frac 1{2c}\left(\frac {1}{\cos\frac{\pi}{c}(a+bi)+\cos\frac{\pi}{c}(a-bi)}\right)\\ &=&\frac 1c \Re\left(\cos\frac{\pi}{c}(a+bi)\right)\\ &=&\frac{2\cos\frac{\pi a}{c}\cosh\frac{\pi b}{c}}{c\left(\cos\frac{2\pi a}{c}+\cosh\frac{2\pi b}c\right)} \end{eqnarray*}$$
ここに, $a=\frac{1}{2\sqrt{2}}, c=\sqrt{2}$を代入して,
$$\begin{eqnarray*} \int_{-\infty}^{\infty}\frac{\cosh\frac{\pi x}{\sqrt{2}}}{\cosh\sqrt{2}\pi x}\cos 2\pi bx\,dx=\frac{\cosh\frac{\pi b}{\sqrt{2}}}{\cosh\sqrt{2}\pi b} \end{eqnarray*}$$
これらを用いて,
$$\begin{eqnarray*} &&\int_0^{\infty}\frac{\cosh\frac{x}{\sqrt{2}}}{\cosh\sqrt{2}x}\frac{dx}{\cosh \alpha x}\\ &=&\frac {\pi}2\int_{-\infty}^{\infty}\frac{\cosh\frac{\pi x}{\sqrt{2}}}{\cosh\sqrt{2}\pi x}\frac{dx}{\cosh \pi\alpha x}\\ &=&\frac {\pi}2\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\frac{\cosh\frac{\pi y}{\sqrt{2}}}{\cosh\sqrt{2}\pi y}\cos 2\pi xy\,dy\frac{dx}{\cosh \pi\alpha x}\\ &=&\frac {\pi}2\int_{-\infty}^{\infty}\frac{\cosh\frac{\pi y}{\sqrt{2}}}{\cosh\sqrt{2}\pi y}\int_{-\infty}^{\infty}\frac{\cos 2\pi xy}{\cosh\pi\alpha x}\,dx\\ &=&\frac{\pi}{2\alpha}\int_{-\infty}^{\infty}\frac{\cosh\frac{\pi y}{\sqrt{2}}}{\cosh\sqrt{2}\pi y}\frac{dx}{\cosh\frac{\pi x}{\alpha}}\\ &=&\frac 1{\alpha}\int_0^{\infty}\frac{\cosh\frac{x}{\sqrt{2}}}{\cosh\sqrt{2}x}\frac{dx}{\cosh\frac{x}{\alpha}} \end{eqnarray*}$$

$$\begin{eqnarray*} \int_0^1\left\lfloor \frac 1x\right\rfloor^{-1}\,dx&=&\int_1^{\infty}\frac 1{\lfloor x\rfloor x^2}\,dx\\ &=&\sum_{n=1}^{\infty}\frac 1n\int_n^{n+1}\frac{1}{x^2}\,dx\\ &=&\sum_{n=1}^{\infty}\frac 1n\left(\frac 1n-\frac 1{n+1}\right)\\ &=&\zeta(2)-1 \end{eqnarray*}$$

$x\to\tanh x$の置換により,
$$\begin{eqnarray*} \int_0^1\frac{x\ln\frac{1+x}{1-x}}{\left(\pi^2+\ln^2\frac{1+x}{1-x}\right)^2}\,dx&=&\int_0^{\infty}\frac{2x}{\left(\pi^2 + 4 x^2\right)^2}\frac{\sinh x}{\cosh^3 x}\,dx\\ &=&\frac 14\frac 1{2\pi i}\int_{-\infty}^{\infty}\left(\frac{1}{(2x-i\pi)^2}-\frac{1}{(2x+i\pi)^2}\right)\frac{\sinh x}{\cosh^3 x}\,dx\\ &=&\frac 1{16}\frac 1{2\pi i}\int_{-\infty} ^{\infty}\left(\frac{1}{\left(x-\frac{i\pi}2\right)^2}-\frac{1}{\left(x+\frac{i\pi}2\right)^2}\right)\frac{\sinh x}{\cosh^3 x}\,dx\\ \end{eqnarray*}$$
ここで, 次のような積分路$C$を考えて, $R\to\infty$とすると,
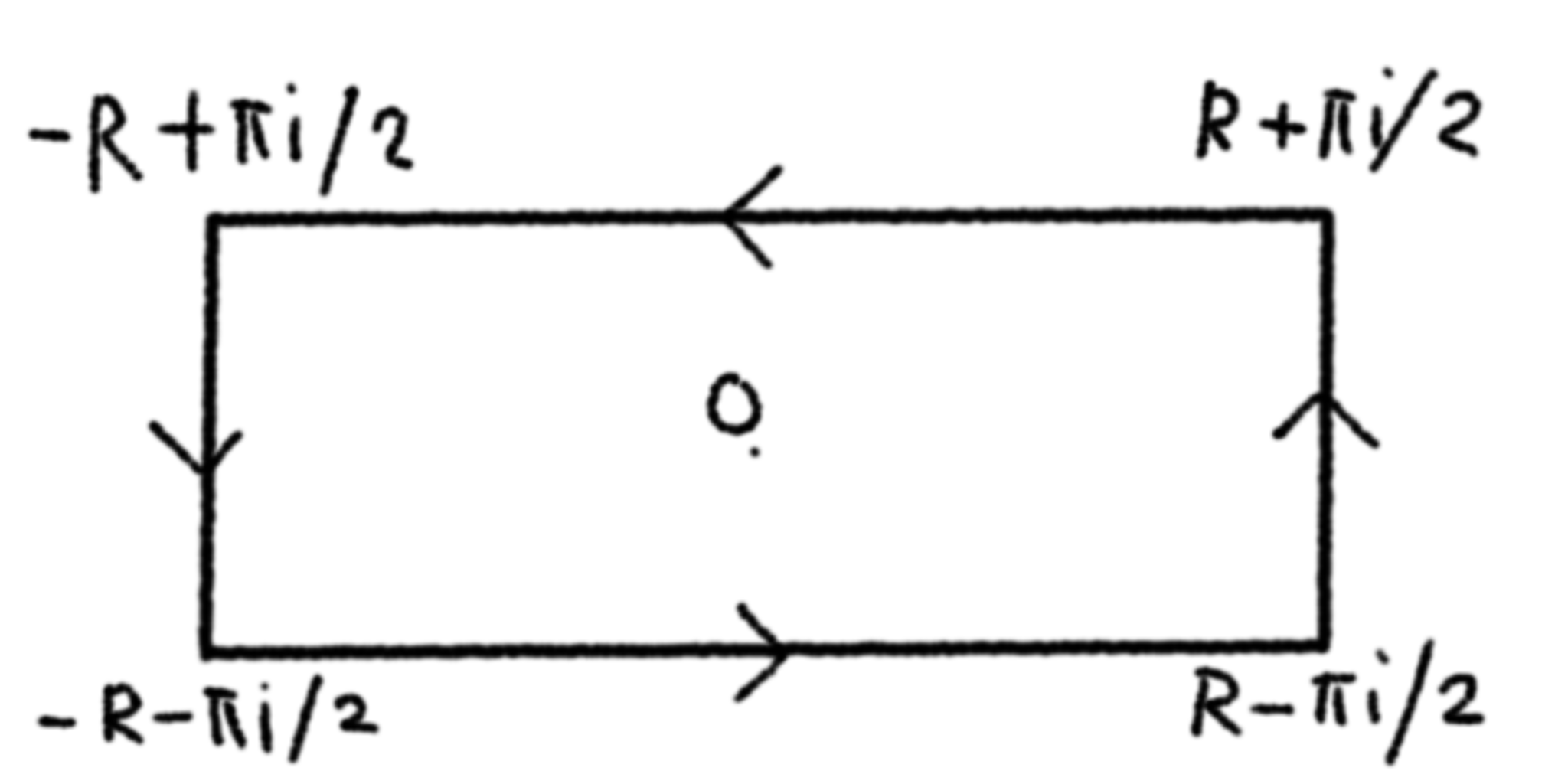積分路1
$$\begin{eqnarray*} \frac 1{2\pi i}\int_{-\infty} ^{\infty}\left(\frac{1}{\left(x-\frac{i\pi}2\right)^2}-\frac{1}{\left(x+\frac{i\pi}2\right)^2}\right)\frac{\sinh x}{\cosh^3 x}\,dx&=&-\frac{1}{2\pi i}\lim_{R\to\infty}\int_C\frac{x^2\cosh x}{\sinh^3 x}\,dx\\ &=&-Res_{x=0}\frac{\cosh x}{x^2\sinh^3x}\\ &=&\frac 1{15} \end{eqnarray*}$$
よって,
$$\begin{eqnarray*} \int_0^1\frac{x\ln\frac{1+x}{1-x}}{\left(\pi^2+\ln^2\frac{1+x}{1-x}\right)^2}\,dx&=&\frac 1{240} \end{eqnarray*}$$