オイラー - ケーニヒスベルクの橋の問題 / THE FIRST PROOF
「ケーニヒスベルクの橋の問題」は当時29歳でサンクトペテルブルクの科学アカデミーに勤めていたオイラーによって1736年に否定的な形で解決されています.そしてこれがグラフ理論的ひいては位相幾何学的発想の起源であるとも言われています.しかしながら,グラフという概念の出現は19世紀後半まで待たねばなりません.すると,最初の証明方法が気になってきます.
まず,問題設定はこうです.プロイセン王国のケーニヒスベルク(東プロイセンの首都で現在のロシア連邦カリーニングラード)を流れるプレーゲル川には図のように7本の橋が架かっていました.では,この7本の橋をちょうど1回ずつ渡って元の場所に戻ってくることは果たしてできるでしょうか.便宜上,それぞれの陸地と橋にアルファベットを割り振っておきましょう.ところで,記事中の図はなんと原論文から転載したものです.
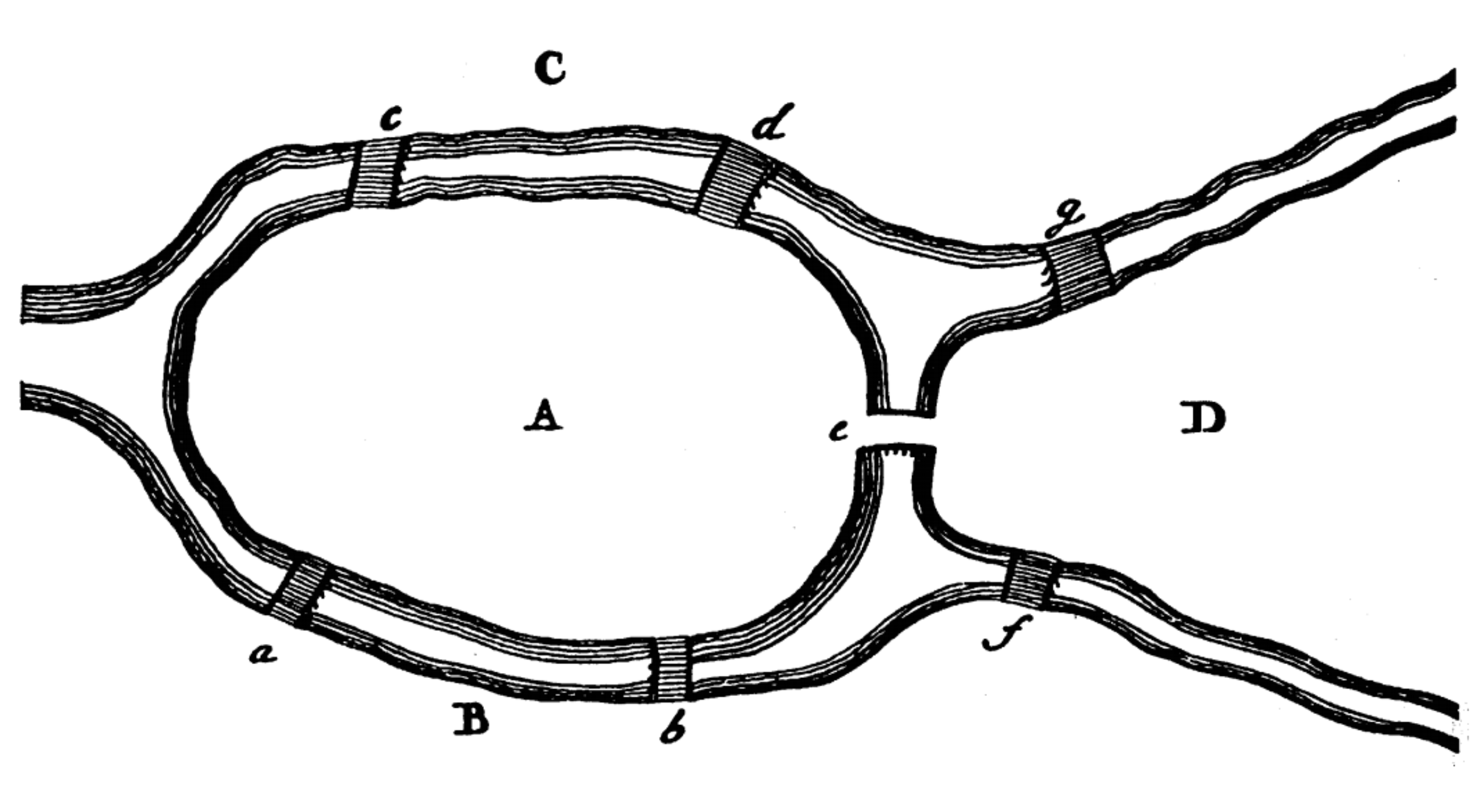
結果をご存知の方は多いと思いますが,オイラーはこれが不可能であることを示したのです.
ケーニヒスベルクの7本の橋をちょうど1回ずつ渡って元の場所に戻ってくるように歩くことはできない.
もちろんこの程度ならばすべての経路の可能性をチェックすれば良いわけですが,それでは骨が折れますし,一般の場合を見据えると現実的に不可能であることはオイラー自身も述べています.この辺りは数学者のスピリットを感じますね.
まず,オイラーは経路を表す方法として橋ではなく陸地の名前を使うことを考えました.例えば,陸地Aから橋aを通って陸地Bに向かう経路を単にABと表わそうということです.すると,7本の橋がありますからこれらをちょうど1回ずつ渡って元に戻る経路からは8文字からなる列が出来上がるはずです.ここで,逆に8文字の列から経路をただ一通りに決定することはできないのですが,それは今回の場合において重大ではないことがすぐに明らかになります.
さて,簡単な例を考えてみるとわかるように,$k$が奇数であるとき,$k$本の橋が架かっている陸地を表す文字は$\frac{k+1}{2}$回出てきます.例えば5つの橋につながる陸地$A$は文字列の中に3回現れます.また,それぞれの陸地に架かる橋の本数を数えるといずれも奇数なので,そこから文字の出現回数を求めると次の表を得ます.
| 陸地の名前 | 架かっている橋の本数 | 文字の出現回数 |
|---|---|---|
| A | 5 | 3 |
| B | 3 | 2 |
| C | 3 | 2 |
| D | 3 | 2 |
ところが,出現すべき回数の総和は9となり,8文字からなる文字列では達成しえないことがわかります.よって主張は示されました.$\blacksquare $
そもそもなぜオイラーはこの問題に注目したのでしょうか.それは,「位置の幾何学(geometriam situs)」,すなわち長さや角度の計測や計算を必要としない問題の典型例だと考えたからです.実際,歩く距離,橋の長さ,道が曲がっているかは(もちろん橋が木造か石造かなどということも!)関係ありません.では「位置の幾何学」はどこからきたのでしょう.ときは遡り,ライプニッツがホイヘンスに宛てた1679年の書簡の中に「位置の解析(analysis situs)」という言葉が導入されます.ただし,これは図形的性質を記号で分析するという後のベクトル解析につながるもののようで,現代的視点ではトポロジーを意図するものではないと考えられることが多いです.一方で,オイラーがこれに影響を受け強く意識していたことはいくつかの書簡からわかっています.
ちなみに,ケーニヒスベルクの問題に続いてオイラーは,$k$が偶数のとき,$k$本の橋が架かる陸地について,そこを出発地とする経路なら$\frac{k}{2}+1$回,そうでない経路なら$\frac{k}{2}$回だけ文字列に現れることを示し,より複雑な陸と橋の配置について考えています.さらには握手補題に相当する主張に至り,最終的には奇数本の橋が架かる陸地が1つの場合を除いて結果を述べているようです.なお,一筆書き可能性に関するオイラーの定理の完全な証明が与えられるのはヒエルホルツァーの遺稿が発見される1870年代のことです.
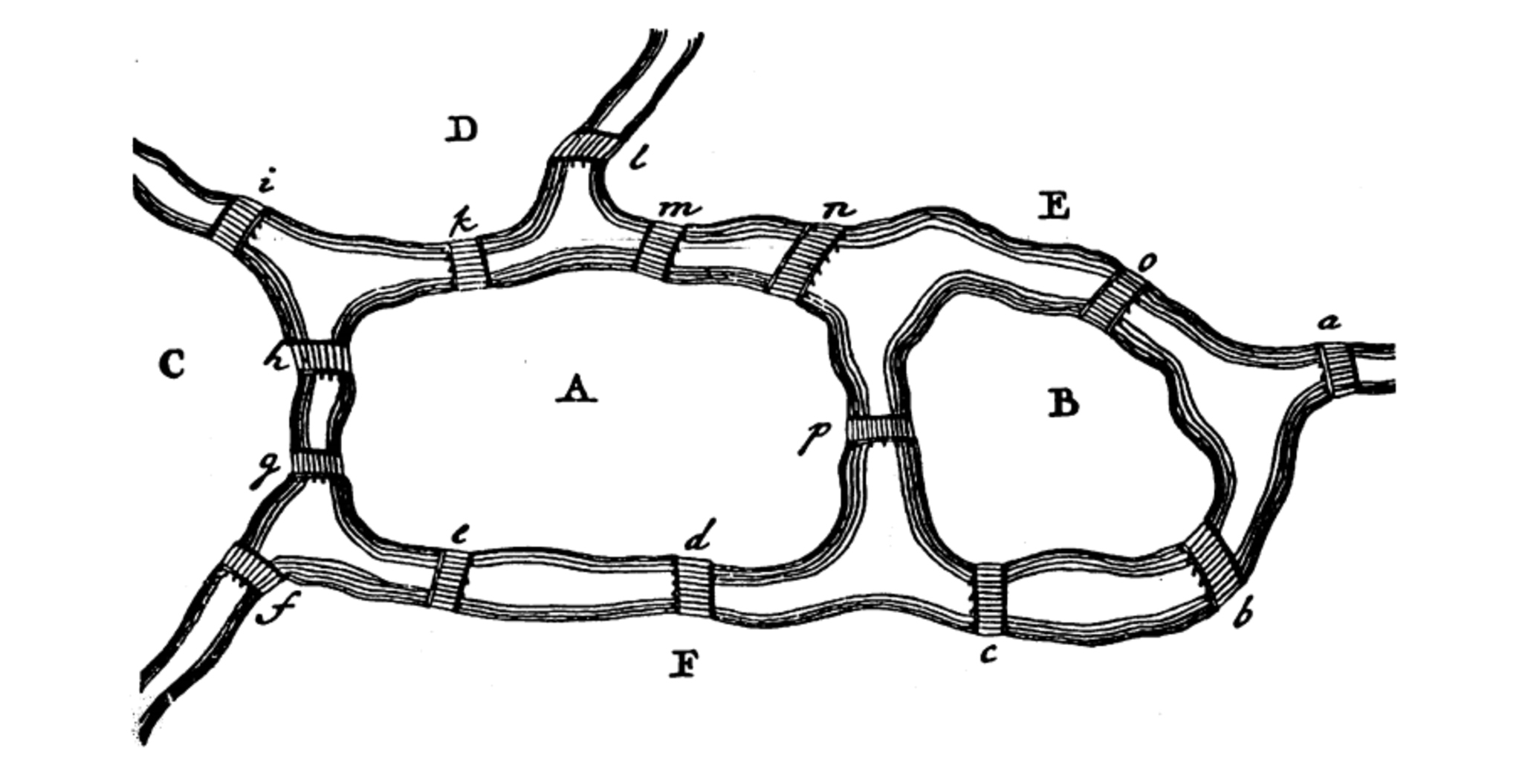
必ずしも体系的でなかったり洗練されていなかったりする最初の証明からは息づかいを感じます.歴史として鑑賞するのも良いですし,研究者目線に立って読んでみるのもまた意義のあることですね.
世間の流行に便乗した記事を今更ながら書きましたが,皆さんが得意な分野で続編を書いていただくことをぜひ期待したいと思います.