みゆ🌹式分数分解でマチンの公式を作ろう♪

マチンの公式

ご存知の方がほとんどかと思われますが、マチンの公式っていうのは

$$\frac\pi4=4\arctan\frac15-\arctan\frac1{239}$$

こーゆーのです。これの右辺をグレゴリー級数とかいう次の式

$$\arctan x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}x^{2n+1}=x-{\frac {1}{3}}x^{3}+{\frac {1}{5}}x^{5}-{\frac {1}{7}}x^{7}+-\cdots\quad(\vert x\vert \lt1)$$

で計算してあげると、なんかめっちゃ速く収束してくれるらしく、円周率を求めるのに適しているんだとか。

このマチンの公式に類似した式はいろいろ発見されていて、いずれも $\displaystyle\frac{\pi}4=\sum_{k=1}^na_k\arctan\frac1{b_k}$ という形をしているのが特徴です。引数の分子が$1$なのは恐らくグレゴリー級数にしたとき少しでも計算をラクにするためかと思われます。

ところで先日、円周率の日に$\xcancel{\arctan}$牛タンを食べに行ったんですよ（唐突）。で、タンだけに$\tan\tan$ と食べて$\tan$ですけど(←)、そのときふと

$$\textcolor{#f07}{\frac\pi2=5\arctan\frac13-\arctan\frac1{26}+\arctan\frac1{2057}}$$

って式を思いついちゃいました。正確にはマチン系の公式にて全ての引数の分子を $1$ にする「逆正接関数の分解定理」とゆーアイデアを思いついてそれを適用してみたわけなんですが、なかなか面白かったので紹介してみたいと思います。(∩´∀｀)∩

作り方

まずは、ベースとなるイメージから(*´∀｀*)b
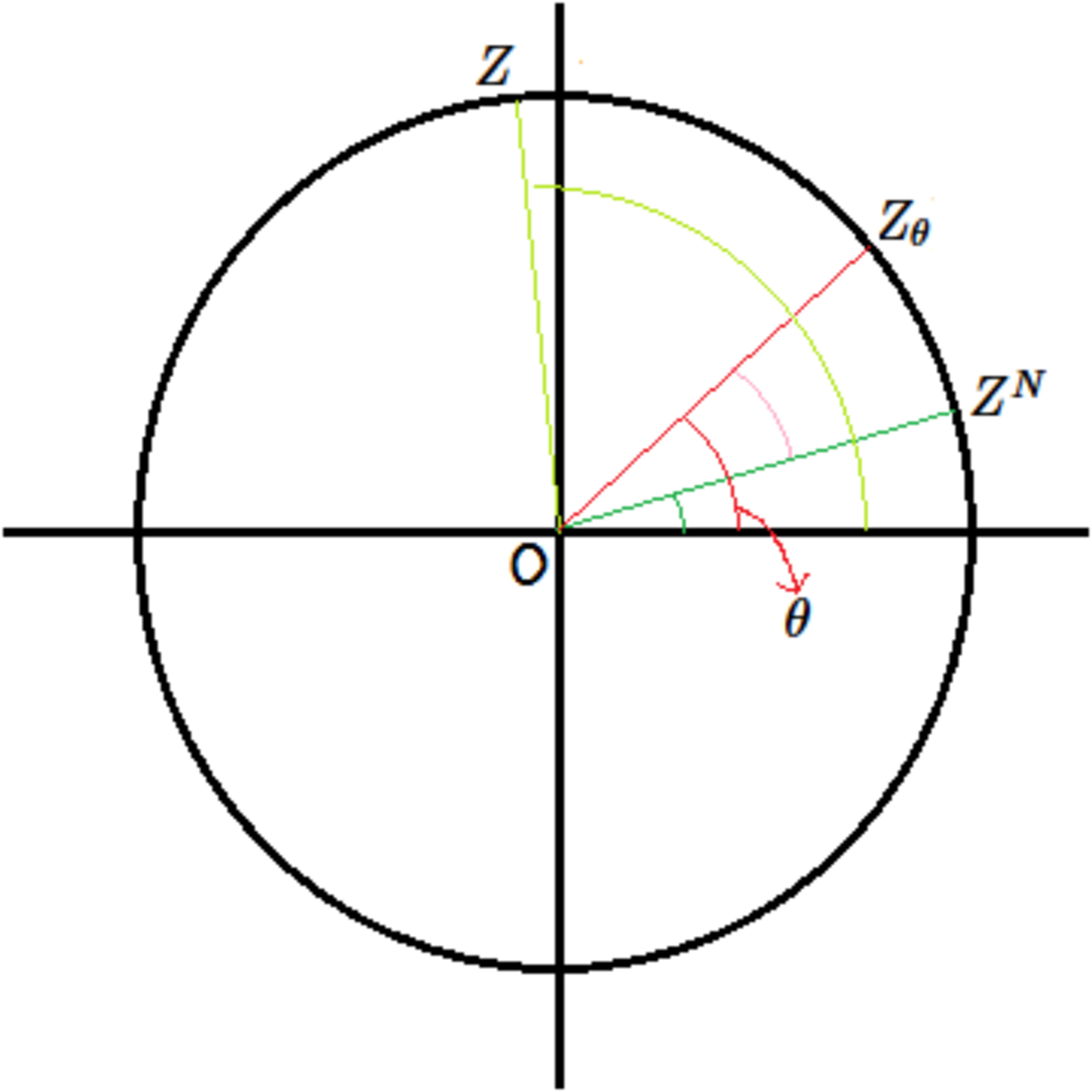イメージ図

$$\begin{align} \mathrm{Arg}~Z_\theta=&\mathrm{Arg}{Z^N}-\mathrm{Arg}{Z^N}+\mathrm{Arg}{Z_\theta}\\ \downarrow&\\ Z_\theta=&Z^N\times\frac{Z_\theta}{Z^N}\\ \downarrow&\\ (\mathrm{Re}~Z_\theta+i~\mathrm{Im}~Z_\theta)=&(\mathrm{Re}~Z+i~\mathrm{Im}~Z)^N\times\frac{\mathrm{Re}~Z_\theta+i~\mathrm{Im}~Z_\theta}{\mathrm{Re}~Z^N+i~\mathrm{Im}~Z^N}\\ =&(\mathrm{Re}~Z+i~\mathrm{Im}~Z)^N\times\frac{\mathrm{Re}~Z^N-i~\mathrm{Im}~Z^N}{\mathrm{Re}~Z^N-i~\mathrm{Im}~Z^N}\cdot\frac{\mathrm{Re}~Z_\theta+i~\mathrm{Im}~Z_\theta}{\mathrm{Re}~Z^N+i~\mathrm{Im}~Z^N}\\ =&(\mathrm{Re}~Z+i~\mathrm{Im}~Z)^N\times\frac{[(\mathrm{Re}~Z^N)(\mathrm{Re}~Z_\theta)+(\mathrm{Im}~Z^N)(\mathrm{Im}~Z_\theta)]+i[(\mathrm{Re}~Z^N)(\mathrm{Im}~Z_\theta)-(\mathrm{Im}~Z^N)(\mathrm{Re}~Z_\theta)]}{(\mathrm{Re}~Z^N)^2+(\mathrm{Im}~Z^N)^2}\\ \downarrow&\\ \arctan\frac{\mathrm{Im}~Z_\theta}{\mathrm{Re}~Z_\theta}=&N\mathrm{\arctan}\frac{\mathrm{Im}~Z}{\mathrm{Re}~Z}+\arctan\frac{(\mathrm{Re}~Z^N)(\mathrm{Im}~Z_\theta)-(\mathrm{Im}~Z^N)(\mathrm{Re}~Z_\theta)}{(\mathrm{Re}~Z^N)(\mathrm{Re}~Z_\theta)+(\mathrm{Im}~Z^N)(\mathrm{Im}~Z_\theta)}\\ \theta=&N\mathrm{\arctan}\frac{\mathrm{Im}~Z}{\mathrm{Re}~Z}+\arctan\frac{\mathrm{Re}~Z^N\cdotp\sin\theta-\mathrm{Im}~Z^N\cdotp\cos\theta}{\mathrm{Re}~Z^N\cdotp\cos\theta+\mathrm{Im}~Z^N\cdotp\sin\theta} \end{align}$$

ここで、第一項目の分子を $1$ にしたいので、$\mathrm{Im}~Z=1$ とすれば

$$\begin{cases} \frac\pi4=N\mathrm{\arctan}\frac{1}{\mathrm{Re}~Z}+\arctan\frac{\mathrm{Re}~Z^N-\mathrm{Im}~Z^N}{\mathrm{Re}~Z^N+\mathrm{Im}~Z^N}\\ \frac\pi2=N\mathrm{\arctan}\frac{1}{\mathrm{Re}~Z}+\arctan\frac{\mathrm{Re}~Z^N}{\mathrm{Im}~Z^N}\\ \pi=N\mathrm{\arctan}\frac{1}{\mathrm{Re}~Z}-\arctan\frac{\mathrm{Im}~Z^N}{\mathrm{Re}~Z^N} \end{cases}$$

となります。$\mathrm{Im}~Z^N\ne(\mathrm{Im}~Z)^N=1$ ってことに注意してね。

もちろん、この時点では二項目の分子が $1$ になってくれる保証はありません。
そこで登場するのが逆正接関数の分解定理を用いた「みゆ式分数分解（牛tan分解）」です！！

証明については $(p+i)(p-i)(pq\pm r+qi)=(p+i)[(pq\pm r)p+q\mp ri]$ と瞬殺させていただくとして、ここで注目すべきは$\text{分母}\equiv\pm r\pmod{\text{分子}}$ を得るところ。

つまり、$q\gt r$ となるような $r$ をとることは確実に可能ですから、同じ操作を再帰的に繰り返すことでいずれは全ての引数の分子を $1$ にできるってわけです。さながら エジプト式分数 みたいな分解方法ですが、みゆ式分数分解ではこれを逆正接関数$\arctan$の引数でやってしまいます(*´艸｀*)

これを使えば、いくらでもマチン系の公式を量産できそうですね。例えば初項を $5\arctan\frac16$ としてみましょうか。$(6+i)^5=5646+6121i$ ですから $5\arctan\frac16=\arctan\frac{6121}{5646}$、分子が分母よりやや大きいことから $45^\circ$ すなわち $\frac\pi4~\mathrm{rad}$ よりやや大きいことが分かります。その差がどのくらいかというと

$$\begin{align} (5646+6121i)\times\overbrace{(1-i)}^{\mathrm{Arg}(1-i)=-\frac\pi4}=&11767+475i\\ \downarrow&\\ \arctan\frac{6121}{5646}\underbrace{-\arctan\frac11}_{-\frac\pi4}=&\arctan\frac{475}{11767} \end{align}$$

それさえ分かれば、あとはひたすら分解していくだけ！

$$\begin{align} \frac\pi4 =&5\arctan\frac16-\arctan\frac{475}{11767}\\ =&5\arctan\frac16-\arctan\frac1{25}-\arctan\frac{54}{147325}\\ =&5\arctan\frac16-\arctan\frac1{25}-\arctan\frac1{2728}+\arctan\frac{13}{401902654}\\ =&5\arctan\frac16-\arctan\frac1{25}-\arctan\frac1{2728}+\arctan\frac1{30915588}-\arctan\frac2{2485011373434113}\\ =&5\arctan\frac16-\arctan\frac1{25}-\arctan\frac1{2728}+\arctan\frac1{30915588}-\arctan\frac1{1242505686717056}+\arctan\frac1{3087640763048447064255689331330}\\ \end{align}$$
Wolfram Alpha 先生による答え合わせ

なんともアメージングですね（汗　計算結果はあってるんですが、項の数も桁の数も尋常じゃない((((；ﾟДﾟ))))

これをもう少しコンパクトにする方法についても一応アイデアはあるのですが、現状ではまだ有用性に乏しいためちゃんと紹介できそうな方法が見つかりましたら続編を書きたいと思います(｡>﹏<｡)ﾉｼ

謝辞

内容について検証くださった nayuta_ito 先生、 博士(笑)のわた 先生、 YouTakaoka 先生 に感謝感謝です♡