相対論： Lorentz変換の導出

はじめに

特殊相対論において重要なLorentz変換を導きます。はじめに「導出ダイジェスト版」を、次に「詳しい導出」を示します。今後相対論に関する記事をいくつか書く（と思う）ので、そのための基礎づくりです。

Lorentz変換の導出は巷に溢れてますが、Mathlog内でこのような基礎的な話題がself-containedになっているのは意味があると思います。また、多少ではありますが独自色を出すようにしてみました。

すでにMathlogでは、wasasekiさんやsubmersionさんなどが相対論に関して書かれています。これらの記事に比べ、本記事は特殊相対論であり、かつかなりやさしいので、一応内容は直交しているかなぁと思います。今後内容が多少なりともかぶるものがあるかもしれませんが、なるべく独自色を出すようにするのでご容赦ください。

Lorentz変換の導出ダイジェスト版

詳しい導出

1. 導出の指導原理

2. 系の設定

空間1次元で考えます。S系(時間座標$t$,空間座標$x$)とS'系(時間座標$t'$,空間座標$x'$)があり、S'系はS系に対して等速直線運動をしています（速度は$v$とします）。また、S'系の空間座標の原点$x'=0$は$t=t'=0$でS系の原点$x=0$と一致しているとします。時刻$t=T$において、$x'=0$は、S系の座標で$x=vT$にあります（図1参照）。この状況で、S系の座標$(t,x)$とS'系の座標$(t',x')$との関係を導きます。以下光速を$c$で表します。

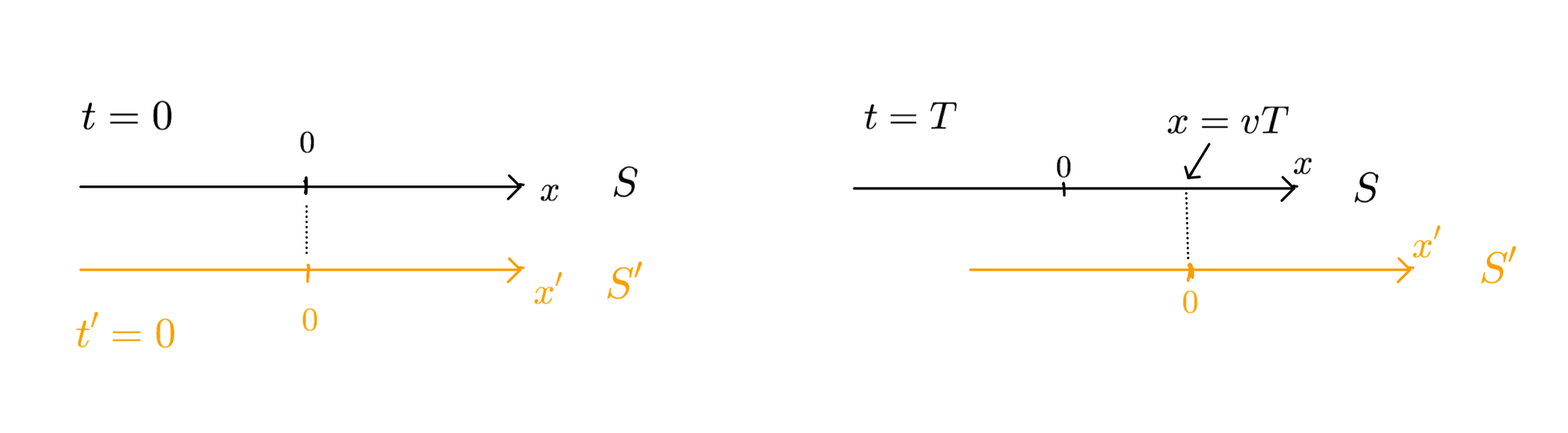S系とS’系の関係

3. Lorentz変換は線形変換

まず最初に、光速度不変という一見不可能にみえる原理を満たすためには、両系の時間が$t'=t$のように等しくては実現できません。そこで、両系の時間と空間が混ざるような変換を考える必要があります。

次に、どんな系から見ても慣性系は慣性系なので、S'系で等速直線運動をしている（$x'$と$t'$は線形）ものは、S系でも等速直線運動をしています($x$と$t$は線形)。このような対等な関係になるには、両系の時空を結びつける座標変換は、時間と空間の1次式であるべきです。すなわちLorentz変換は
\begin{align} \begin{pmatrix} t'\\x' \end{pmatrix} = \begin{pmatrix} p & q\\ r &s \end{pmatrix} \begin{pmatrix} t\\x \end{pmatrix} \end{align}
のように表せます。$p,q,r,s$は$v$(と光速$c$)に依存したパラメータです。

4. S'系の原点をS系から見たときの条件、およびその逆

S'系の原点はSの原点$(t,x)=(0,0)$と一致し、その後速度$v$で動いているから、$(t',x')=(t',0)$はS系から見ると$(t,x)=(t,vt)$と一致しています。これらを上の式に代入すれば
\begin{align} \begin{pmatrix} t' \\ 0 \end{pmatrix} = \begin{pmatrix} p & q\\ r & s \end{pmatrix} \begin{pmatrix} t \\ vt \end{pmatrix} \end{align}
となります。よって、
\begin{align} 0&=rt+svt\\ s&=-r/v \end{align}
となります。

逆にS'系からS系を見ると、その空間座標の原点$x=0$は$(t',x')=(t',-vt')$と一致しています。逆行列を計算することで、$(t,x)$を$(t',x')$で表すと
\begin{align} \begin{pmatrix} t\\x \end{pmatrix} = \frac{1}{ps-qr} \begin{pmatrix} s && -q\\ -r && p \end{pmatrix} \begin{pmatrix} t'\\x' \end{pmatrix} \end{align}
となります。これに$(t,x)=(t,0),(t',x')=(t',-vt')$を入れると
\begin{align} \begin{pmatrix} t\\0 \end{pmatrix} = \frac{1}{ps-qr} \begin{pmatrix} s && -q\\ -r && p \end{pmatrix} \begin{pmatrix} t'\\-vt' \end{pmatrix} \end{align}
が成立します。よって
\begin{align} 0&=-rt'-pvt'\\ p&=-r/v \end{align}
となります。

5. 光速度不変の原理を課す

次に、「光速度不変性」を課します。今、S系で$(t,x)=(0,0)$から光が放たれたとします。時刻$t$における光の波面の位置は$x=ct$です。任意の慣性系から見て光の速度が$c$というのが光速度不変性です。よって、同じ光の波面が、S'系から見ると$x'=ct'$の位置に存在します。よって
\begin{align} x'=ct'=c(pt+qx)=c(pt+qct) \end{align}
となります。一方
\begin{align} x'=rt+sx=rt+sct \end{align}
なので、
\begin{align} r+sc=cp+qc^2 \end{align}
が成立します。$p=s=-r/v$なので、これを代入し
\begin{align} r-rc/v&=-rc/v+qc^2\\ q&=r/c^2 \end{align}
となります。まとめると
\begin{align} p=s=-r/v, q=r/c^2 \end{align}
これらを用いると
\begin{align} \begin{pmatrix} t' \\x' \end{pmatrix} = \begin{pmatrix} -r/v & r/c^2\\ r & -r/v \end{pmatrix} \begin{pmatrix} t \\x \end{pmatrix} \end{align}
となります。

6. $r$の決定

最後に残ったパラメータ$r$を決定しましょう。
ここで、相対性原理をもちいて、$(t,x)$を$(t',x')$で表しましょう。S'からS系を見ると速度$-v$で移動しています。よって上式で$(t',x')$と$(t,x)$を入れ替え、かつ$v\rightarrow -v$とした式が成立するはずです。ただし気をつけなければならないことがあります。それは$r$が$v$に依存していることです。よって上式を
\begin{align} \begin{pmatrix} t' \\x' \end{pmatrix} = \begin{pmatrix} -r(v)/v & r(v)/c^2\\ r(v) & -r(v)/v \end{pmatrix} \begin{pmatrix} t \\x \end{pmatrix} \ \ \ (1) \end{align}
のように$r$の$v$依存性を陽に書くと（物理では"explicit"のことを陽(あらわ)と表現します）、
\begin{align} \begin{pmatrix} t \\x \end{pmatrix} = \begin{pmatrix} r(-v)/v & r(-v)/c^2\\ r(-v) & r(-v)/v \end{pmatrix} \begin{pmatrix} t' \\x' \end{pmatrix} \ \ \ (2) \end{align}
が成立します。

さて、$r(-v)$と$r(v)$の関係を考えます。
\begin{align} x'=r(v)t+s(v)x \end{align}
で、$v$の符号を反転すると$x'=r(-v)t+s(-v)x$ですが、速度を反転することは、時間反転して$v$を正のままにしたものと等しいはずです。よって
\begin{align} x'=r(-v)t+s(-v)x=-r(v)t+s(v)x \end{align}
これが任意の$t,x$で成立するので、
\begin{align} r(-v)=-r(v), s(-v)=s(v) \ \ \ (3) \end{align}
となります。

　ちなみに、このことから$v=0$とすると$r(0)=-r(0)$より$r(0)=0$となります。これは$v=0$で$t'=t, x'=x$となるべしという条件、すなわち
\begin{align} \begin{pmatrix} t'\\x' \end{pmatrix} = \begin{pmatrix} p(0) & q(0)\\ r(0) &s(0) \end{pmatrix} \begin{pmatrix} t\\x \end{pmatrix} =\begin{pmatrix} t\\x \end{pmatrix} \\ \therefore p(0)=s(0)=1, q(0)=r(0)=0 \end{align}
とconsistentです。

Eq.(1)(2)(3)から
\begin{align} \begin{pmatrix} t' \\x' \end{pmatrix} &= \begin{pmatrix} -r(v)/v & r(v)/c^2\\ r(v) & -r(v)/v \end{pmatrix} \begin{pmatrix} t \\x \end{pmatrix} \\&＝ \begin{pmatrix} -r(v)/v & r(v)/c^2\\ r(v) & -r(v)/v \end{pmatrix} \begin{pmatrix} r(-v)/v & r(-v)/c^2\\ r(-v) & r(-v)/v \end{pmatrix} \begin{pmatrix} t' \\x' \end{pmatrix} \\ &＝ \begin{pmatrix} -r(v)/v & r(v)/c^2\\ r(v) & -r(v)/v \end{pmatrix} \begin{pmatrix} -r(v)/v & -r(v)/c^2\\ -r(v) & -r(v)/v \end{pmatrix} \begin{pmatrix} t' \\x' \end{pmatrix} \\&= \begin{pmatrix} r(v)^2/v^2-r(v)^2/c^2 & 0\\ 0 & -r(v)^2/c^2+r(v)^2/v^2 \end{pmatrix} \begin{pmatrix} t' \\x' \end{pmatrix} \end{align}
より（以下$r(v)$を$r$と書く）
\begin{align} &r^2/v^2-r^2/c^2=1\\ &\therefore r=\pm \frac{v}{\sqrt{1-\beta^2}}, \ \ \beta:=v/c \end{align}
となります。符号は$t'=-rt/v+rx/c^2$が$v\rightarrow 0$で$t'=t$になることからマイナスを取ります。
$p=s=-r/v, q=r/c^2$なので
\begin{align} p&=s=\frac{1}{\sqrt{1-\beta^2}}\\ q&=-\frac{\beta}{c\sqrt{1-\beta^2}} \end{align}
です。

7. Lorentz変換の最終形

まとめると、Lorentz変換のパラメータは
\begin{align} r&=-\frac{v}{\sqrt{1-\beta^2}} \ \ \ (\beta:=v/c),\\ p&=s=-r/v, \ q=r/c^2 \end{align}
と決定されました。最終的に

となります。

8. Remarks

導出のまとめ

どのようにLorentz変換を導出したかをまとめておきます

1. 時間1次元、空間1次元のLorentz変換は、$(t,x)$と$(t',x')$の間の線形変換である
   ...4 parameters
2. S'系の$x'=0$はS系の座標では$x=vt$という条件、およびその逆(S系の$x=0$をS'系の座標で表すと$x'=vt'$)の条件を課す
   ...2 constraints
3. 光速度不変の原理を課す
   ...1 constraint。2.のconstraintsと合わせて変数を減らすことにより、未知定数が1つになる。
4. 相対性原理より、$(t',x')$を$(t,x)$で書いた表式(Lorentz変換)とその逆の表式(逆Lorentz変換)は、速度$v$を$-v$にすることで結びつく。こうして得られたLorentz変換と逆Lorentz変換を連続して施したとき恒等変換になる条件を課す
   ... 1 constraint。これですべてのパラメータが決定された

Lorentz変換は単なる座標変換ではない!

Lorentz変換は、単なる座標変換の式ではありません。

$(t,x)=(t',x')=(0,0)$を考えます。例えば、S系にいる人がある駅におり、S'の人は電車に乗っていて、電車の中の人と駅の人がすれ違う瞬間を考えます。さて、電車の中の$x'$軸（空間軸）、$t'$軸（時間軸）はそれぞれ$t'=0, x'=0$の線で表されます。これらの軸をS系の座標で表すとそれぞれ
\begin{align} ct=\beta x \ \ \ (x'\text{軸}),\\ ct=\frac{1}{\beta}x \ \ \ (t'\text{軸}) \end{align}
の直線になります（図2参照）。これが単なる変数変換なら、「Sから見て斜行したS'という座標の$t'=0, x'=0$の線を$(t,x)$で表した」という以上のものではないです。このような見方、言い換えれば相対論以前のニュートン的絶対時間では、時間座標$t$こそが本当の時間座標で、$(t',x')$はあくまでそれを変数変換したものにすぎないということになります。例えるなら、極座標で何かを表したからといって、それで表現されたものが曲がるわけではないように、$(t',x')$も単なる変数変換により作られた変数という捉え方を、あなたはするかもしれません。しかしLorentz変換はそのような単なる座標変換ではありません。ここで相対性原理が重要になります。相対性原理とは、全ての慣性系が同等だという原理であり、よってS系とS'系は対等です。S'にいる人はあくまで$(t',x')$の座標で生きており、それはS系に生きる人と完全に対等です。よって、例えば、S'の空間軸、すなわちS'にいるものにとっての同時の線というのは、本当に$t'=0$に、つまりは$ct=\beta x$上にあるのです。

言い換えれば、Lorentz変換に上記のような物理的意味をもたせるのが相対性原理です。

S系とS'系の時間・空間軸。時間軸を$ct$にすることで、次元を空間軸と一致させています。

光速度不変性および相対性原理のチェック

そうなるように作ったのだから当然ではありますが、一応、Lorentz変換における光速度不変性および相対性原理を確かめておきましょう。
(1) 光速度不変性のチェック
これはLorentz変換の式に$x=ct$を入れ、$t',x',t$の連立方程式にして、$t$を消去すれば良いです。Lorentz変換の式に$x=ct$を入れると
\begin{align} t'&=\gamma t - \gamma\beta t\\ x'&=-\gamma v t + \gamma c t\\ \gamma&:=\frac{1}{\sqrt{1-\beta^2}} \end{align}
ですから、$x'=ct'$となることが確かめられます。
(2) 相対性原理のチェック
これはLorentz変換の逆行列
\begin{align} \frac{1}{ps-qr} \begin{pmatrix} s & -q\\ -r & p \end{pmatrix} \end{align}
と（言うなればtrivialな逆変換）、Lorentz変換を$v\rightarrow -v$として得られた逆Lorentz変換（相対性原理を用いて導いた逆変換）が一致することを確かめればよいです。
簡単な計算から
\begin{align} \frac{1}{ps-qr}=1 \end{align}
が確かめられるので、Lorentz変換の逆行列は
\begin{align} \frac{1}{ps-qr} \begin{pmatrix} s & -q\\ -r & p \end{pmatrix} = \begin{pmatrix} s & -q\\ -r & p \end{pmatrix} \ \ \ (4) \end{align}
となります。
一方、
\begin{align} p&=s=\gamma,\\ q&=-\frac{v}{c^2}\gamma, \\ r&=-v\gamma \end{align}
より、$v\rightarrow -v$に対して
\begin{align} p,s&\rightarrow p,s\\ q,r&\rightarrow -q, -r \end{align}
なので、Lorentz変換は$v\rightarrow -v$に対し
\begin{align} \begin{pmatrix} p & q\\ r & s \end{pmatrix} = \begin{pmatrix} s & q\\ r & p \end{pmatrix} \rightarrow \begin{pmatrix} s & -q\\ -r & p \end{pmatrix} \end{align}
となります。これはEq.(4)と等しいので、題意は示されました。

遠いところほど時間がずれる

上の方で、両系の原点が一致する時空点において、S'系の同時刻($t'=0$)はS系の座標で
\begin{align} ct=\beta x \end{align}
上にあることに言及しました。この式からわかることは、$\beta$が大きい程=$v$が大きい程、また、遠くであればあるほど、両系の同時のズレが大きくなるということです。例えば$\beta=0$なら両系の時間軸はともに$t=0$で表されて同じです。また、$\beta>0$でも$x$が小さければ、時間のズレは小さいです。逆に、たとえ両系の相対速度が小さくても、$x$が十分大きいと、時間のズレは非常に大きくなります。

この"同時刻の相対性"が、特殊相対性理論において我々の直感が通用しなくなる大きな原因です。

不変距離を用いた計算

今回、4.において、$x=ct$かつ$x'=ct'$が成立することを光速度不変の原理として採用しましたが、これに代わって、（3次元+時間の時空における）不変距離
\begin{align} \Delta s^2=(c\Delta t)^2-\Delta x^2-\Delta y^2-\Delta z^2 \end{align}
が慣性系に依存しないという条件、すなわち
\begin{align} (ct)^2-x^2-y^2-z^2=(ct')^2-x'^2-y'^2-z'^2 \ \ \ (5) \end{align}
を用いても良いです。空間1次元にするには、$y,z,y',z'=0$とするか、または$x$方向にのみ速度をもつとして、$y=y', z=z'$としても良いです(厳密には$x$方向にのみ速度をもつ時$y=y', z=z'$となることは証明すべきことですが)。

Eq.(5)に、4.で導いた
\begin{align} p=s=-r/v \end{align}
を代入すると
\begin{align} c^2\left(\frac{r^2}{v^2}-\frac{r^2}{c^2}\right)t^2 -2c^2\left(\frac{rq}{v}-\frac{r^2}{c^2v}\right)tx +c^2\left(q^2-\frac{r^2}{c^2v^2}\right)x^2=c^2t^2-x^2 \end{align}
がなりたち、これが任意の$t,x$で成立することから
\begin{align} r&=-\frac{v}{\sqrt{1-\beta^2}},\\ q&=-\frac{v}{c^2\sqrt{1-\beta^2}} \end{align}
が導けます。この方法だと、6.で行った$r$に関する変換性等の考察がいらないので、そういう意味ではちょっと楽です。