放物線を使った2次の相加平均と相乗平均の大小関係の証明

まずは放物線$ y= x^{2} $上の点$ A( a,a^{2} ) $,点$ B( b,b^{2} ) $における接線の方程式を求めます.
$ y= x^{2} $を微分すると,
$$ 　　y^{\prime}=2x $$
よって点Aにおける接線の方程式は,
$$ y=2a(x-a)+ a^{2} $$
$$ y=2ax-a^{2} 　\cdots \cdots① $$
同様に点Bにおける接線の方程式も求めると,
$$ y=2bx-b^{2} 　\cdots \cdots② $$
となります.
次に①,②の交点をPとし,Pの座標を求めます.
①,②を連立して$y$を消去すると,
$$ 2ax-a^2=2bx-b^2 $$
$$ 2(a-b)x=(a+b)(a-b) $$
　$a \neq b$として$ x= \frac{ \large{a+b} }{ \large{2} } $
これを①に代入して,
$$ y=2a(\frac{a+b}{2}) -a^{2}=ab $$
ゆえに点Pの座標は,
$$ P(\frac{a+b}{2},ab) $$
となります.
$ a=b $のときは,点Pは接点A,Bそのものとみなします.
不等式に出てくる数字が登場しました.
ここで今までの結果を図で見てみましょう.
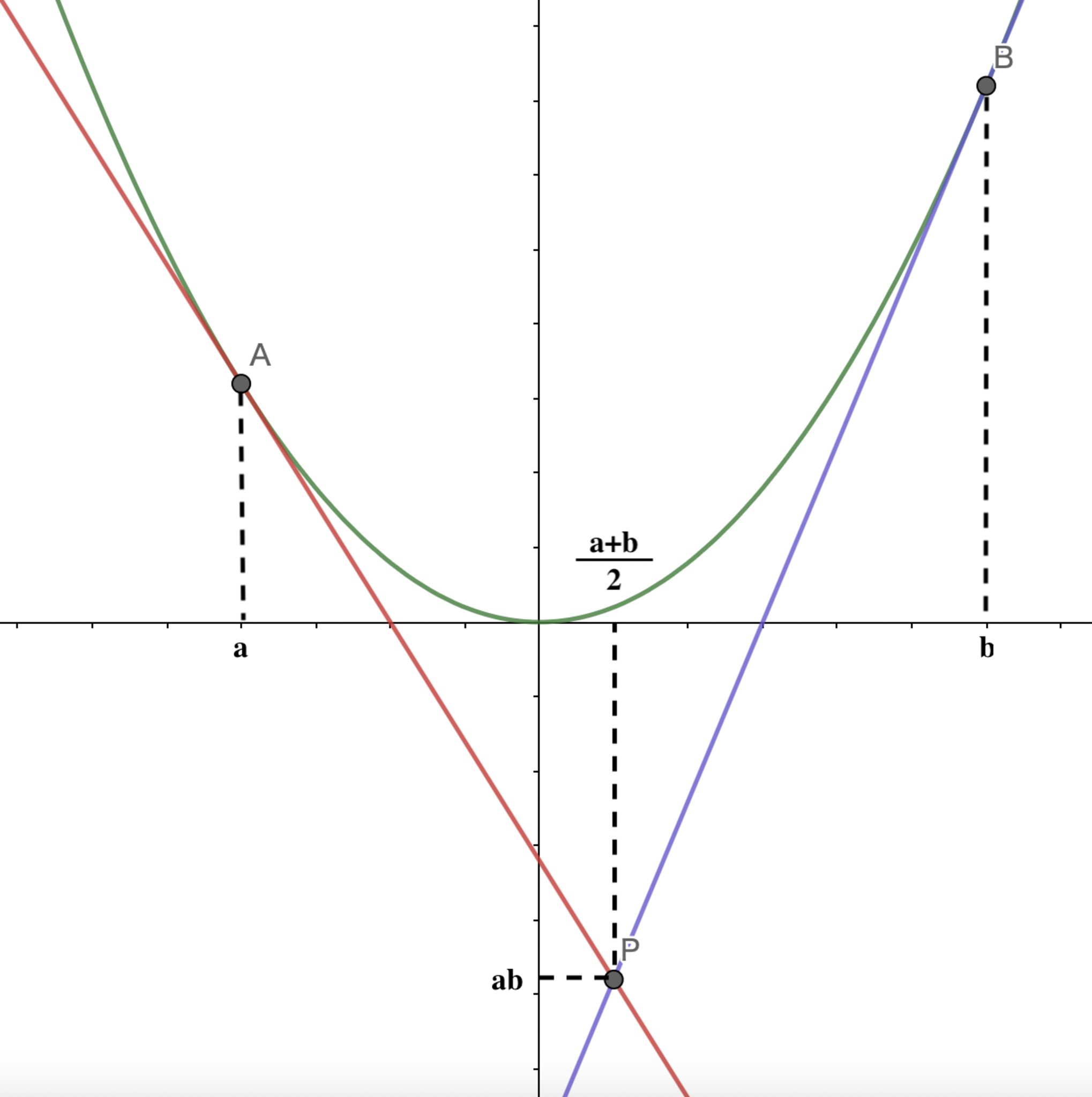図
さていよいよ示します.
ここで,$ f(x)=x^{2} $とおきます.
すると放物線は下に凸なので,点Pは常に放物線上またはその下側にあることから次の不等式が成り立ちます.
$$ f( \frac{a+b}{2} ) \geqq ab $$
$$ ( \frac{a+b}{2} )^{2} \geqq ab $$
あと一歩です.
$ a,b $を$ a>0,b>0 $で選べば,両辺の平方根をとって,
$$ \frac{a+b}{2} \geqq \sqrt{ab} $$
また,等号が成り立つのはPが放物線上にあるとき,つまり$ a=b $だとわかりますね.
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(証明終わり)