モーリーの定理を証明する

三角形$ABC$の内角の3等分線の,辺に近い2つずつの交点を図のように$I_1,I_2,I_3$とし,外角の3等分線についても同様に,交点を$J_1,J_2,J_3$とする.また,直線$BI_1,J_1C$の交点を$P_1$,直線$CI_1,J_1B$の交点を$P_2$とし,同様に点$Q_1$,$Q_2$,$R_1$,$R_2$を定める.$\angle{BAI_3}=\angle{I_3AI_2}=\angle{I_2AC}=\alpha$,$\angle{CBI_1}=\angle{I_1BI_3}=\angle{I_3BA}=\beta$,$\angle{ACI_2}=\angle{I_2CI_1}=\angle{I_1CB}=\gamma$とする.

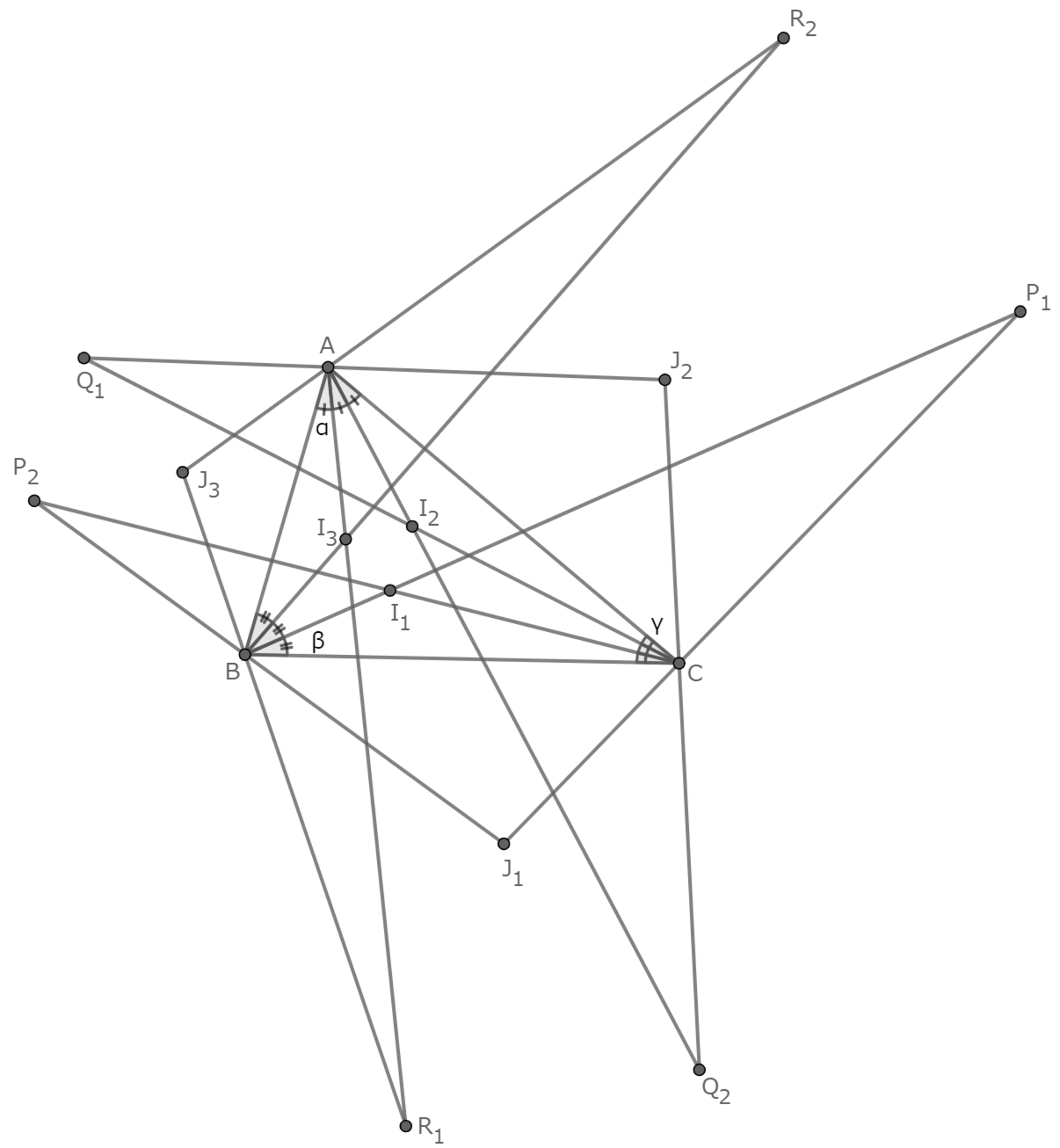点の定義
簡単な角度計算により$BP_1C\sim BAI_3\sim Q_2AC$,$CP_2B\sim CAI_2\sim R_1AB$,$BR_2A\sim BCI_1\sim Q_1CA$
がわかり,$B,C,P_1,P_2$と$C,A,Q_1,Q_2$と$A,B,R_1,R_2$の共円もわかる.

$P_1P_2$と$CJ_2,BJ_3$の交点を$J_2',J_3'$とする.このとき$B,C,P_1,P_2$の共円から$\angle{J_2'P_1C}=\angle{J_1BC}$
$\angle{J_2'CP_1}=\angle{J_1CB}$から$J_2'CP_1\sim J_1CB$ $\therefore$$P_1C:J_2'C=BC:J_1C$
また,$\angle{P_1CB}=\angle{J_2'CJ_1}=120^{\circ}+\gamma$から$P_1CB\sim J_2'CJ_1$
同様に$P_2BC\sim J_3'BJ_1$

$\angle{J_3'BJ_1}+\angle{J_1P_1J_3'}=(120^{\circ}+\beta)+(60^{\circ}-\beta)=180^{\circ}$
より$B,J_1,P_1,J_3'$は共円.$\therefore$$\angle{J_3'P_1B}=\angle{J_3'J_1B}=\gamma$
$\angle{AR_2B}=\angle{J_3'R_2B}=\gamma=\angle{J_3'J_1B}$より$B,J_1,R_2,J_3'$は共円.よって$B,J_1,P_1,R_2,J_3'$は共円.
$\angle{R_2J_1J_3'}=\angle{R_2P_1J_3'}=\angle{R_2P_1J_1}-\angle{J_2'P_1C}=(180^{\circ}-\angle{R_2BJ_1})-\angle{J_1BC}=60^{\circ}$,
$\angle{J_2'J_1J_3'}=\angle{BJ_1C}-\angle{BJ_1J_3'}-\angle{CJ_1J_3'}=60^{\circ}$より$\angle{R_2J_1J_3'}=\angle{J_2'J_1J_3'}=60^{\circ}$
から$J_1,J_2',R_2$は共線

$A,B,R_1,R_2$の共円から$\angle{ABJ_3'}=\angle{J_3'R_2R_1}=60^{\circ}-\beta$
$\angle{J_3'R_2J_1}=\angle{J_3P_1J_1}=60^{\circ}-\beta$　から$\angle{J_3'R_2R_1}=\angle{J_3'R_2J_1}$
よって$R_2,J_1,R_1$は共線　　　$J_1,J_2',R_2$の共線から$R_1,J_1,J_2',R_2$は共線
$\therefore$$\angle{BJ_1R_1}=180^{\circ}-\angle{BJ_1J_2'}=120^{\circ}-\gamma$
$BJ_1R_1\sim BJ_3A$から$\angle{BJ_3'A}=120-\gamma$
ここで,$\angle{AJ_3B}=\angle{AJ_3'B}=120^{\circ}-\gamma,\angle{ABJ_3}=\angle{ABJ_3'}$から$J_3=J_3'$
同様に$Q_2,J_1,J_3,Q_1$は共線で,$J_2=J_2'$

簡単な計算により,$J_1J_2J_3,J_1R_1Q_2,J_2P_1R_2,J_3Q_1P_2$は正三角形であることがわかる.

$AI_3B\sim ACQ_2$から$AI_3:AB=AC:AQ_2$,$AI_2C\sim ABR_1$から$AI_2:AC=AB:AR_1$
この2式から$\displaystyle \frac{AI_3}{AR_1}=\frac{AI_2}{AQ_2}$を得る.$\therefore$$I_3I_2\parallel R_1Q_2$　　　　同様に$I_1I_3\parallel P_1R_2,　I_2I_1\parallel Q_1P_2$
$R_1Q_2\parallel J_3J_2,　P_1R_2\parallel J_1J_3,　Q_1P_2\parallel I_2I_1$から$I_3I_2\parallel J_3J_2,　I_1I_3\parallel J_1J_3,　I_2I_1\parallel J_2J_1$
$J_1J_2J_3$は正三角形なので$I_1I_2I_3$も正三角形.よって示された.

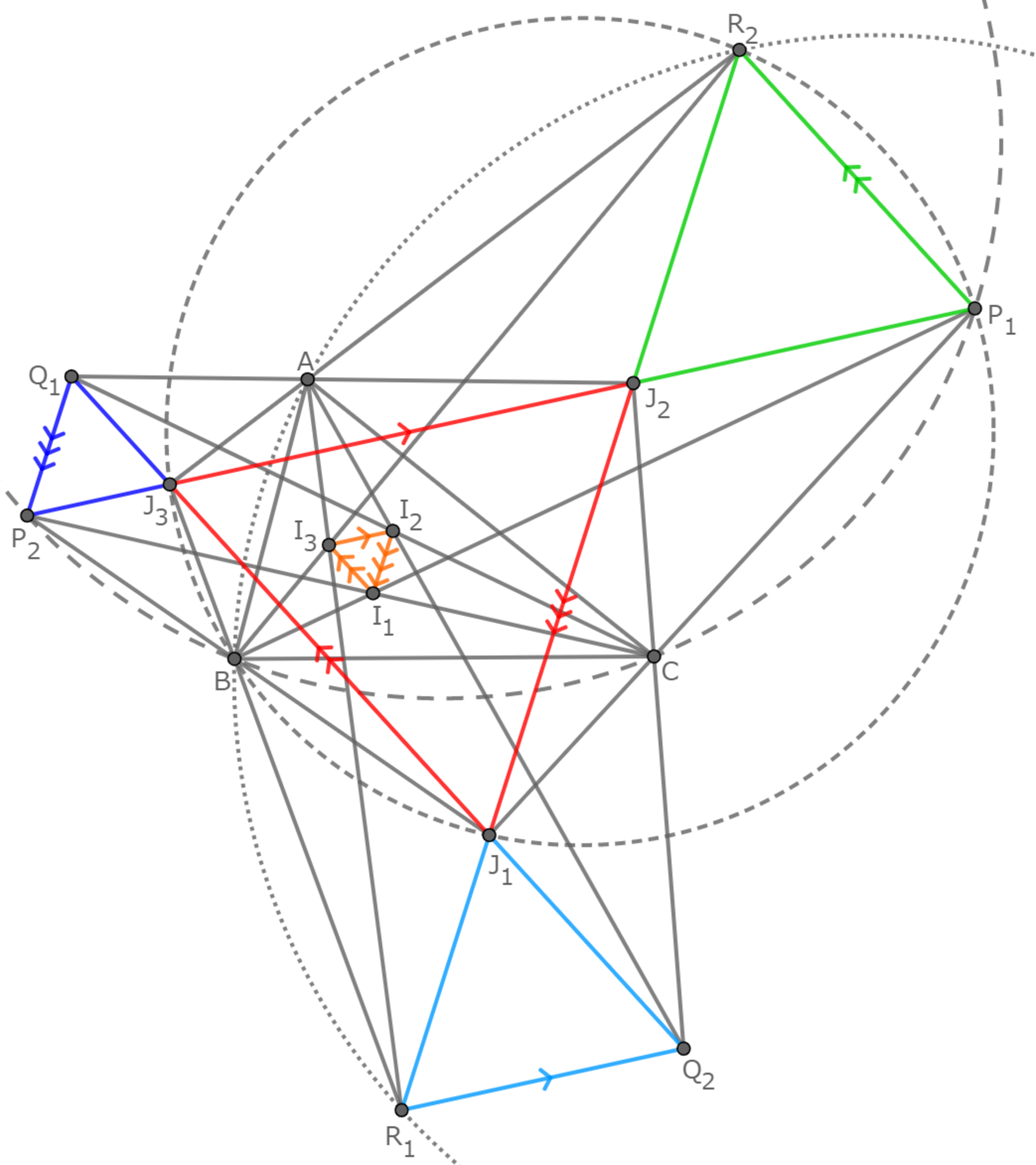完成図