群・環・体 超超超入門 <群編>
みなさんこんにちは。
まず初めに私の主張を1つ。
この世にある「OO入門」と書かれた数学書、大体は取っ付き難く書かれている。
これは真です。(大体って書いてあるから)
この主張はより高度な数学をやろうとすればするほど真に近づいていきます。(?)
特に大学数学は取っ付きやすさや、分かりやすさを軽視したものがとても多いと思います。
高校数学ではとても分かりやすいものがいくらでもあると言うのに。
故に、私はもっと入門に相応しいものを作ろうと思いました。それが超超超入門です。
その第一歩として群・環・体の話を書こうと思います。
本稿の最終目標としては、準同型定理の概要とその凄さを分かることになります。
長々と書きましたが、以上で前書きは終わりです。
群の世界へ行ってらっしゃい。
基本的なスタンスとして、万人にわかるように書いていきますので、皆様が分かる部分は読み飛ばしていただくと良いと思います。
逆に、定義のところでは専門的な記号や言葉をガンガン使っていきますが、無理に読もうとしなくても大丈夫です。
また、この記事は概要の掴みやすさのみに力を注いでいるため、厳密性を損なっている部分が多々あります。ご了承ください。
序章
群とは集合の上位互換である。
まずは群についてお話しします。
その切り口はこう。
昔々...
ある数学者は考えました。
集合って色んなものを一息に扱えてめっちゃ便利なんだよな〜
でも、なんかうまく使いきれてない気がする。うまく使えばきっと、集合は世界を一度に扱えるはずなんだ。
ただ、「何かしらの集まり」ってだけだと漠然すぎる...
そうだ！ちょっとしたルールを付加しよう！
そうしてできたものが群です(この昔話は大部分が虚偽です)。
より具体的には、
単位元と逆元がその集合内に存在するような演算があるとき、その集合を、その演算に関しての群と呼ぶ。
今から、演算・単位元・逆元について述べるので、今はまだ何言ってるか分からなくても問題ありません。むしろ分かっていたら怖いです。
集合のどの要素2つ(同じでも良く、順序付き)に対しても定義されていて、その演算結果が、集合の要素になるようなもの。
定義中の「順序付き」と言う言葉は、$1*2$と$2*1$を別物として考えると言うことです。本稿ではこのことをしばしば無視して話を行いますが、とても重要なことですので、忘れないようにしましょう。
例)$*$が引き算である時$1*2=-1\neq 2*1=1$
演算は足し算、引き算、掛け算、割り算が代表的だと思います。
けれど、ここで言う演算とは何でもありです。
とにかく集合の要素を操作していればいい。
たとえば、「くっつける」、「入れ替える」、「0にする」、「左側を100乗して右側は無視」などなど。
どの集合の中の要素二つに対して操作しても、その結果が集合の中にあれば、何でも演算です。
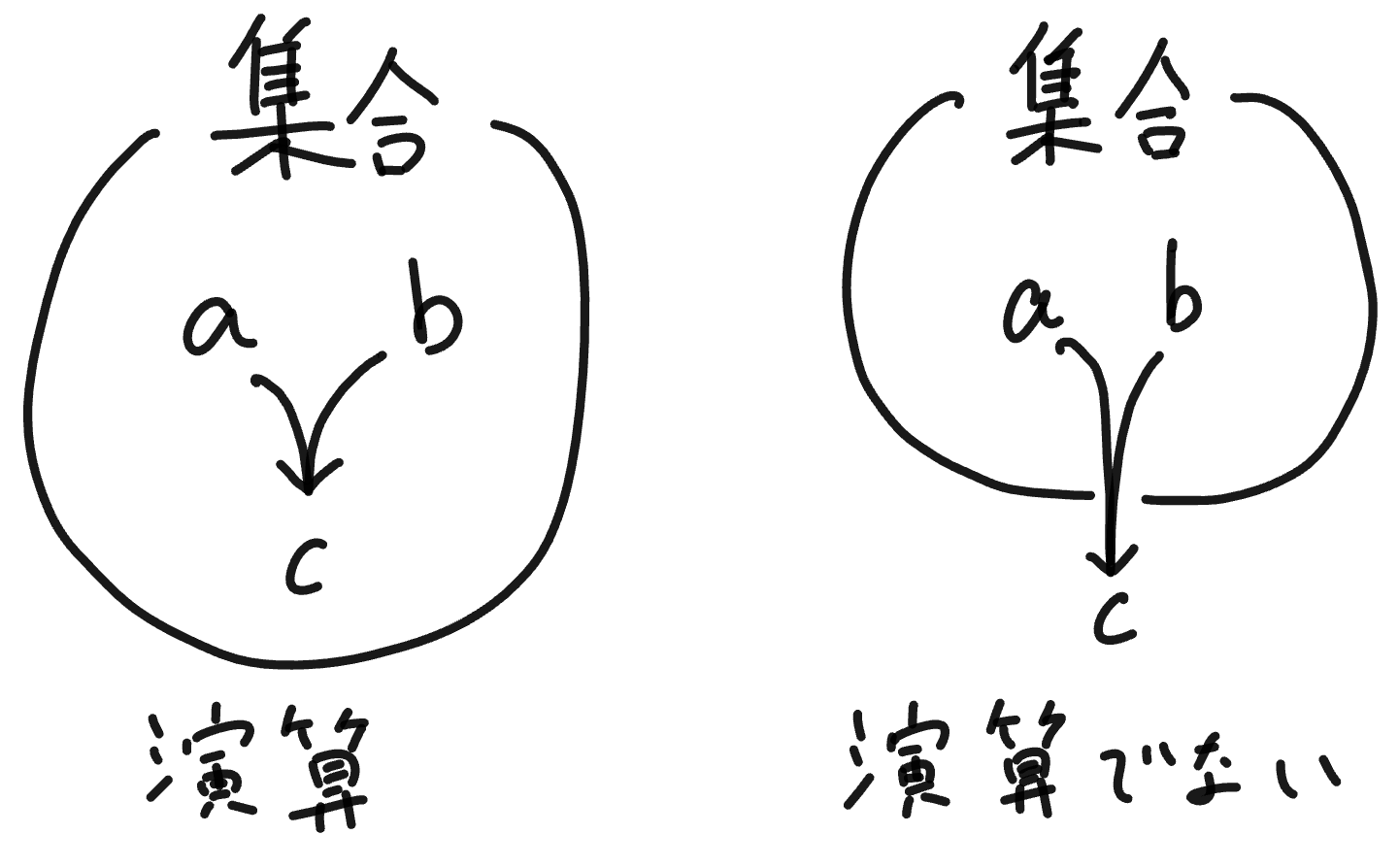演算のイメージ
集合の要素のうち、どの要素$a$と演算を行っても、演算結果が$a$になるものを単位元と呼ぶ
続きまして、単位元です。
単位元はなにも変えない要素のことです。
例えば、
$$5\times 1 =5,10\times 1=10$$
のようにどんな数字に$1$をかけても、意味がありません。
そのため、掛け算という演算に関して、$1$は単位元です。
他にも、$$0+5=5,93+0=93$$のようにどんな数字に$0$を足しても、意味がありません。
そのため、足し算という演算に関して、$0$は単位元です。
こんな感じで、元に戻る要素のことを単位元と呼びます。
ある要素$a$に関して他の要素$b$が逆元であるとは、$a$と$b$の演算結果が単位元になることをさす。
つまり、掛け算で言うところの$1/a$,足し算で言うところの$-a$です。
何の捻りもない。
元に戻ればそれが逆元。
単位元と逆元がその集合内に存在するような演算があるとき、その集合を、その演算に関しての群と呼ぶ。
さて、演算・単位元・逆元のイメージを掴めたところで、群の定義をもう一度見てみましょう。
今なら分かるはずです。
ある集合に対して、演算があって、それに合わせて単位元、逆元がある。
例を見てみると、より分かりやすいと思います。
例えば
整数の集合は足し算に関して群です。
単位元は$0$,$a$の逆元は$-a$。
他にも、正の実数の集合は掛け算に関して群です。
単位元は$1$,$a$の逆元は$\frac1a$
ここまでが群の定義でした。ここから先の話で群が何かわからなくなったら直ぐに見直してみると良いでしょう。
部分群
群$\mathbf{G}$の部分集合$\mathbf{H}$が$\mathbf{G}$の演算に関してが群である時、$\mathbf{H}$を$\mathbf{G}$の部分群と呼ぶ
演算$*$に関する群$\mathbf{G}$の部分群$\mathbf{H}$による左剰余類全体の集合$\mathbf{G}/\mathbf{H}$とは
$$\mathbf{G}/\mathbf{H}=\{a\mathbf{H},b\mathbf{H},... \}$$
のことであり、右剰余類全体の集合$\mathbf{H}\textbackslash \mathbf{G}$とは
$$
\mathbf{H}\textbackslash \mathbf{G}=\{\mathbf{H}a,\mathbf{H}b,...\}
$$のことである。
ここで、$a,b,...$は$\mathbf{G}$の要素である。
また、$a\mathbf{H}=\{a*h|h$は$\mathbf{H}$の要素$\}$であり、$a$に関する左剰余類と呼ぶ。
同様に、$ \mathbf{H}a=\{h*a|h$は$\mathbf{H}$の要素$\}$であり、$a$に関する右剰余類と呼ぶ。
いきなり二つ新しい単語を出してみました。特に剰余類については何言ってんだって感じだと思います。私も最初そうでした。ですがここで諦めずにもうちょっと頑張りましょう。
また、右剰余類か、左剰余類かは本稿では気にしなくても良いです。そういう言い方もあるぐらいな認識で問題ありません。
まずは部分群の話から。
群とはそもそも、ある集合のことをより詳しく考えよう、という試みで生まれたものです。
そのため、群がどんな要素からできているか、つまり、群の構造にとても興味があるわけです。
そこで、その群の中でより簡単な部分を見出すために、部分群が生まれました。
100個の物を考えるより50個の物を考える方が、50個の物を考えるより3個の物を考える方が楽ですから、より小さい群を考えたわけです。
その名の通り、群の一部であって、なおかつ、それ自身も群であるもののことです。
ちなみに、元々の群自身や単位元も部分群の一つです。
続きまして、群について話す際の最初のボトルネックである、剰余類についてです。
定義のところでは小難しく書きましたが、実はそんなに難しい物ではありません。
先ほども述べた通り、私たちはいま群の構造に興味があるのです。
剰余類は群の構造を知るための道具です。どういう道具かというと、グループ分けするという道具です。
ここでは数学の言葉を使わずに説明したいと思います。
高校(中学校)の教室を思い浮かべてください。40人の生徒がいます。
しかし、当然ながら40人が1まとまりに行動するということはあり得ません。
いくつかの2~5人くらいの小グループに分かれています。
時には10人くらいの少し大きなグループがあるかもしれません。
生徒一人一人で見るのではなく、これらのグループを見る、それが剰余類を使って行いたいことです。
より正確には、これらのグループ一つ一つのことを剰余類と呼びます。
剰余類はあくまでグループなので、集合のことを指しています。なので、定義中に出てきていた$\mathbf{G}/\mathbf{H}$はグループを集めたものなのです。
いうなれば集合の集合です。
これが剰余類のイメージです。理解できたでしょうか。
$\mathbf{G}$を群、$\mathbf{H}$を$\mathbf{G}$の部分群とする。任意の要素$a$について$a\mathbf{H}=\mathbf{H}a$となる時、$\mathbf{H}$を$\mathbf{G}$の正規部分群と呼ぶ。
小難しく名前をつけていますが、さきほど登場した右剰余類と左剰余類を区別しなくても良いような部分群のことを正規部分群と呼びます。
ようするに、剰余類を扱う際に便利な部分群のことですね。
ちょっと優秀な部分群。
とても規則的な部分群、故に、正規部分群。
この認識で問題ありません。
これは以下の剰余群のところで活躍します。
$\mathbf{H}$を$\mathbf{G}$の部分群とする。任意の$\mathbf{G}$の要素$a,b$に対し、剰余類の集合$\mathbf{G}/\mathbf{H}$が以下で定義される演算$*$に関して群である時、剰余群と呼ぶ。$$a\mathbf{H}*b\mathbf{H}=ab\mathbf{H}$$
特に、$\mathbf{H}$が正規部分群であるとき、$\mathbf{G}/\mathbf{H}$は剰余群になる。
剰余群というものが出てきました。
これはとても喜ばしいものです。
何故か。
何度も言いますが私たちは群の構造に興味がある。むしろそれ以外には興味がないほどに。
剰余群は
群を小グループに分けても、群になっている。
そう主張しているのです。
つまり、大きな元々の群ではなく、より小さい群を考えれば元々の群の構造を知ることができるのです。
これは部分群でも当てはまるのではないかと考える人もいると思います。
確かにそうです。
しかし、部分群は元々の群の一部しか扱えていないのです。
対して、剰余群は元々の群全体を扱いつつ、より少ない要素で考えられる。
$$ $$
例を見てみるとその凄さが分かると思います。
$$ $$
整数の集合を$\mathbb{Z}$とします。
これは、足し算に関して群になっています。
単位元$0$が存在し、任意の要素$a$に対して、逆元$-a$が存在するためです。
この時、$5\mathbb{Z}=\{...,-10,-5,0,5,10,...\}$は正規部分群であるため、
$
\mathbb{Z}/5\mathbb{Z}=\{0+\mathbb{Z},1+\mathbb{Z},2+\mathbb{Z},3+\mathbb{Z},4+\mathbb{Z}\}
$
は群になります。
ここで$5+\mathbb{Z}$や$-2+\mathbb{Z}$などが書かれていないのは、
$5+\mathbb{Z}=0+\mathbb{Z}$であり、$-2+\mathbb{Z}=3+\mathbb{Z}$だからです。(わからない方は少し考えてみよう)
$5$と$-2$以外の整数についても同様です。
さて、話を戻しましょう。
$\mathbb{Z}/5\mathbb{Z}$を見てください。
整数が無限個あるにも関わらず、要素がたったの5つしかありません!!!!!!!!!!!!!!!
無限個に比べれば、5つというのはとても扱いやすく、性質も分かりやすいはずです。
これが、剰余群の力なのです。
すばらしいでしょう？
準同型写像
演算$\circ$に関する群$\mathbf{G}$と演算$*$に関する群$\mathbf{G'}$に対して、$\mathbf{G}$から$\mathbf{G'}$への写像$f$が
$f(a\circ b)=f(a)*f(b)$
を満たす時、$f$を$\mathbf{G}$から$\mathbf{G'}$への準同型写像という。
ついに準同型写像までやってきました。
私たちの目標が準同型定理なので、あと少しなことが名前からも窺えますね。
ここででてきた写像とは、要するに関数のことです。
ただ、関数とは数値を入れると数値が返ってくるもののことですが、群は数字の集合とは限らないため、別の名前が必要になったのです。そして生まれたのが写像です。
写像は何かしらを入れると、何かしらが返ってきます。
何かしらは何かしらです。三角形でも、りんごでも、ゴリラでも、あなたでも、watashiでも。もちろん、数字もokです。
写像にとっての関数は果物にとってのりんごですね。
閑話休題
準同型写像で行いたいことは、群と群を比較して、構造を客観的に見るということです。
もしも、とても構造が似ている群があったならば、そちらを調べることで元々の群の構造が、完全にではなくとも少しは分かりそうな気がしませんか？
しかし、ただ眺めるだけで群を比較できるなんて、そんな素晴らしいことはありません。
群を比較するために$f$という、2つの群をお互いに結びつけるものがあるのです。
$$f(a\circ b)=f(a)*f(b)$$
というのは、$f$が2つの群を結びつけていると言っているのです。
より具体的には、$f$の計算前に演算を施しても、$f$の計算後に演算を施しても、同じだ、と主張しているわけです。
$f$はとても有用なものなので、準同型写像という名前がついたのです。
$f$を$\mathbf{G}$から$\mathbf{G'}$への準同型写像とする。この時、$\mathbf{G}$の部分集合
$\{a|f(a)$が$\mathbf{G’}$の単位元$\}$
を$f$の核と呼び、$\mathrm{ker}f$と書く。
特に、$\mathrm{ker}f$は$\mathbf{G}$の正規部分群である。
$f$を$\mathbf{G}$から$\mathbf{G'}$への準同型写像とする。この時、$\mathbf{G'}$の部分集合
$\{f(a)|a$が$\mathbf{G}$の要素$\}$
を$f$の像と呼び、$\mathrm{Im}f$と書く。
特に、$\mathrm{Im}f$は$\mathbf{G'}$の部分群である。
核と像が登場しました。
これはどっちがどっちかごっちゃになってしまうきがするので、ここはイラストで覚えるのが良いでしょう。
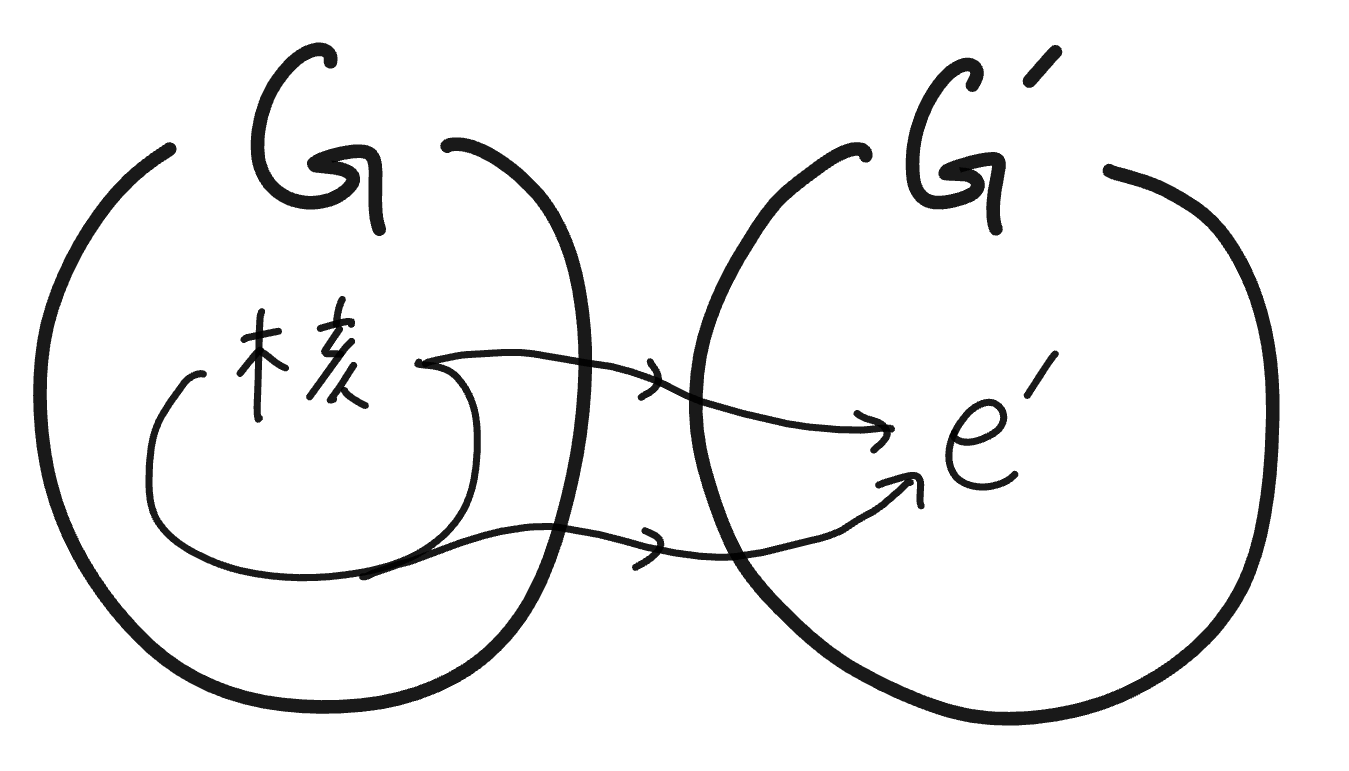核のイメージ
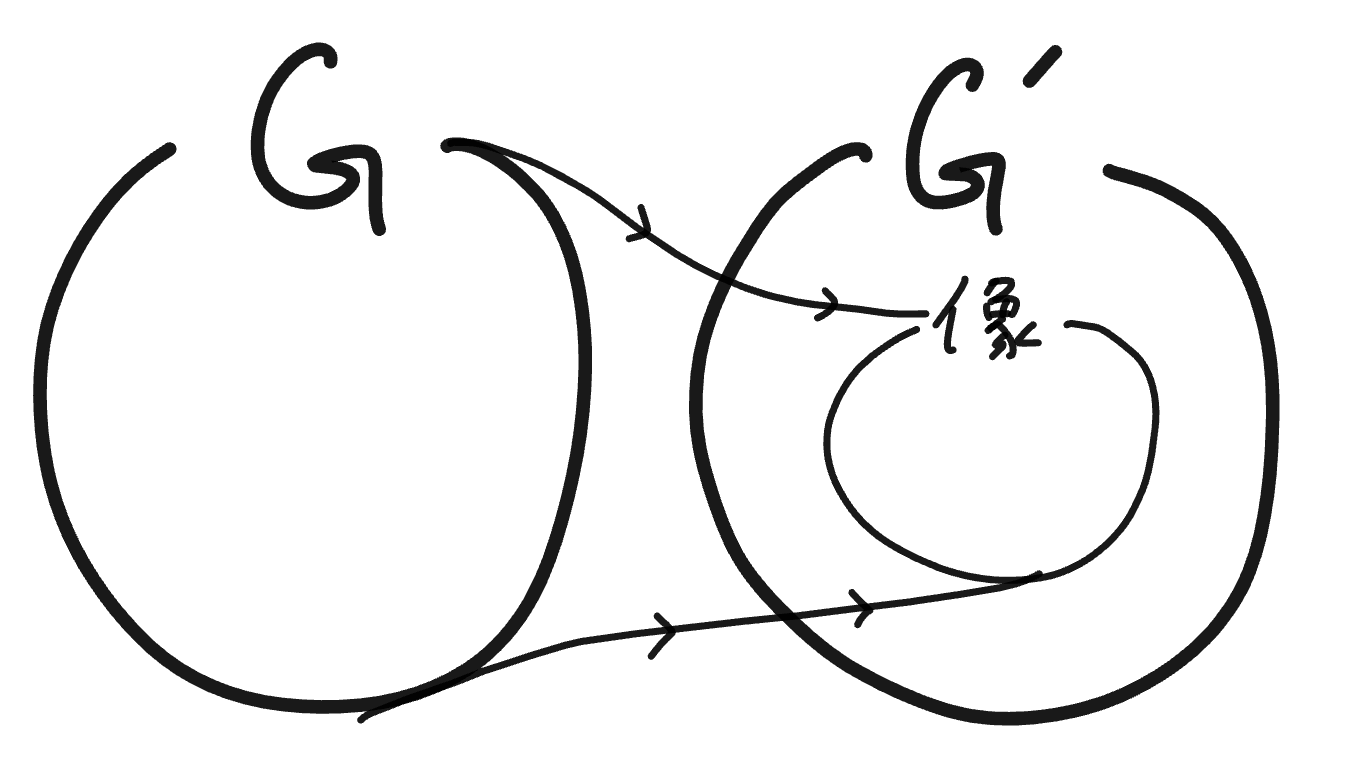像のイメージ
先ほどは$f$を結びつけているものという漠然とした解釈でしたが、ここでは$f$はレンズ的な役割を果たします。
核も像も、$f$というレンズを使って$\mathbf{G}$(と$\mathbf{G'}$)を覗いている感覚です。
どういうことかというと、$f$というレンズを使うと、$\mathrm{ker}f$は$\mathbf{G’}$の単位元$e’$に重なって見えるわけです。
単位元というのは当然その群の中心的な存在、言い換えれば核($\mathrm{ker}$のことじゃない)となるような存在ですから、このネーミングにも納得できる気がしてきませんか？
同様に、$f$というレンズを使うと、$\mathrm{Im}f$は$\mathbf{G}$全体に重なって見えるわけです。
それゆえに、$\mathrm{Im}f$は$\mathbf{G’}$に映し出された$\mathbf{G}$の像($\mathrm{Im}$のことじゃない)のような気がしてきます。
さて、ついに本稿の目的であった準同型定理に入ります。が、その前に、一つ単語を追加しておきたいと思います。
同型写像という言葉です。
$\mathbf{G}$から$\mathbf{G'}$への準同型写像のうち、核と$\mathbf{G}$の単位元が等しく、像と$\mathbf{G’}$が等しくなるようなものを同型写像と呼ぶ。
準同型写像のうち、最も便利であると言っても過言ではありません。
ただでさえ、正規部分群という便利な存在であった核が単位元という明確なものになり、部分群であった像が$\mathbf{G'}$全体になるのですから便利でないはずがありません。
同型写像の便利な性質の一つとして、$\mathbf{G}$の要素と$\mathbf{G’}$の要素は1対1対応をしているという事が挙げられます。
即ち、片方を調べると即座にもう片方がわかるという事です。
何度でも思い出しましょう。私たちが群を扱う目的はその集合の構造を知ることです。であれば、どちらか一方を調べるだけでどちらも分かるというのは、とても喜ばしいことなのです。
また、$\mathbf{G}$と$\mathbf{G’}$の間に同型写像が存在する時、$\mathbf{G}$と$\mathbf{G’}$は同型であると呼びます。
$f$を$\mathbf{G}$から$\mathbf{G'}$への準同型写像とする。
この時、$\mathrm{Im}f$と$\mathbf{G}/\mathrm{ker}f$は同型である。
あの...この定理強すぎないですか？
準同型写像を適当に持ってきたら、いきなり同型の群が現れた。
しかも、$\mathbf{G}/\mathrm{ker}f$なんて、剰余類のところでも述べた通り、より少ない個数で$\mathbf{G}$を観察する事ができるものなんです。
ですから、この定理の主張するところは、より小さく、要素が少ない所で、これら群について、とても都合の良い条件の下で比較・検討して良いと言っているわけです。
良いですか？
何度でも説明しましょう。
$ \mathbf{G}$と$\mathbf{G’}$はほとんど無作為に持ってきました。
でも無作為に持ってきているから、どんな関係性があるかなんて分かりようがない...
もしも、これら二つの関係性が瞬く間に分かるようになるような、便利な道具があったなら...
そんな夢のような道具、あるんです!!!
それ即ち、準同型定理!!!
例を挙げましょう。
実数の集合$\mathbb{R}$は足し算$+$と掛け算$\times$という演算に関して、それぞれ群である。
$\circ$を$+$、$*$を$\times$とすれば、実数の集合$\mathbb{R}$から実数の集合$\mathbb{R}$への写像$f(x)=2^x$が
$$f(x\circ y)=f(x)*f(y)\Leftrightarrow f(x+y)=2^{x+y}=2^x\times 2^y=f(x)\times f(y)$$
を満たしているため、$f$は$\mathbb{R}$から$\mathbb{R}$への準同型写像である。
ここで、$\mathrm{Im}f=\mathbb{R}_{>0}$であり、$\mathrm{ker}f=\{0\}$であるため、
$\mathbb{R}_{>0}$と$\mathbb{R}/\{0\}=\mathbb{R}$は同型である。
ここで、$\mathbb{R}_{>0}$は正の実数の集合とする。
これは、すなわち、実数全体を考えるのではなく、正の範囲だけを考えれば十分であるということを示唆しています！
実数の集合は足し算$+$に関して群であり、複素平面の単位円上の点の集合$\mathbb{T}$は掛け算$\times$に関して群である。
$\circ$を$+$、$*$を$\times$とすれば、$\mathbb{R}$から$\mathbb{T}$への写像$f(x)=e^{ix}=\cos{x}+i\sin{x}$は、
$$
f(x\circ y)=f(x)*f(y)\Leftrightarrow f(x+y)=e^{x+y}=e^x\times e^y=f(x)\times f(y)
$$
より準同型写像である。
ここで、$\mathrm{Im}f=\mathbb{T}$であり、$\mathrm{ker}f=2\pi\mathbb{Z}$であるから、
$\mathbb{T}$と$\mathbb{R}/2\pi \mathbb{Z}$は同型である。
ここで、$\mathbb{Z}$は整数の集合とする。
この例では、実数全体と単位円を比較するのではなく、$\mathbb{R}/2\pi \mathbb{Z}$と単位円を比較すれば十分であるということを言っているのです！！
$\mathbb{R}/2\pi \mathbb{Z}$は少しイメージを掴みにくいですが、ざっくり言うと、$0$~$ 2\pi$の範囲だけを考えると言うことです(詳細は剰余類の欄を参照)。多少複雑になりますが、実数全体を扱うことに比べれば、圧倒的に扱うべき範囲が狭くなっています!!!
こんな夢のようなことを考えているのが群論なのです。
最後に
本稿では群論基礎についてイメージを行うことを主軸として解説を行ってきました。そのため、本稿の初めにも書いた通り、どうしても厳密性をなおざりにしてしまう箇所が多々あります。従って、是非とも入門書をお近くの書店や図書館などで入手して、読むことをお勧めしたいと思います。
また、当然ながら本稿で伝える事ができる魅力には限りがあります。実際、本稿では群論の魅力の1%も伝えられていないと思います。
そのため、本稿に書かれている内容が群論の全てではないどころか、ほんの一部にしか過ぎないことを、強調したいと思います。
最後に、本稿を書くにあたって様々な情報源を用いました。その全ての作成者、及び、本稿を読んでいただいた全ての読者と、この場を提供していただいたMathlogに感謝して、終わりにしたいと思います。
ありがとうございました。
参考文献
新妻弘, & 木村哲三. (2023). 群・環・体 入門 (25th ed.). 共立出版株式会社.
結城浩. (2018). 数学ガール ガロア理論(5th ed.). SBクリエイティブ株式会社.
たくみ.[予備校のノリで学ぶ「大学の数学・物理」].(2020,Dec 9).【大学数学】群論入門⑨(準同型定理)【代数学】[video].youtube.
https://www.youtube.com/watch?v=TNapSZBEZX4&t=2548s
この記事を高評価した人
この記事に送られたバッジ
投稿者
