Lie代数メモ
あいさつ
んちゃ
この記事はLie代数についてYANASANが学習した事をメモしたものになります。
メモなので、多少ごちゃついてますが読んでもらえると嬉しいです。
- カンドル
- Lie代数
- ルート
- 戸田格子への応用
- $E_{ij}=(\delta_{ik}\delta_{jl})_{kl}$
カンドル
$X$を集合、そして写像$s:X\ni x\mapsto s_{x}\in Map(X,X)$を考える。
この写像$s$が下記の性質を満たす時$(X,s)$を対称空間と言う。
\begin{eqnarray}
\left\{
\begin{array}{l}
(S1)\quad \forall x\in X:s_{x}(x)=x\\
(S2)\quad \forall x\in X:s_{x}^{2}=id\\
(S3)\quad \forall x,y\in X:s_{x}\circ s_{y}=s_{s_{x}(y)}\circ s_{x}
\end{array}
\right.
\end{eqnarray}
また、上記の条件$(S2)$を次の条件$(S2^{'})$に置き換えたものをカンドルと言う。
\begin{equation}
(S2^{'})\quad \forall x\in X:s_{x}は全単射
\end{equation}
任意の集合$X$は$s_{x}=id$とした時対称空間となる。
$\mathbb{R}^{n}$は、$s_{x}(y)=2x-y$とすると対称空間になる。
[S1]$s_{x}(x)=2x-x=x$
[S2]$s_{x}^{2}(y)=2x-(2x-y)=y$
[S3]
\begin{eqnarray}
s_{x}\circ s_{y}(z)&=&2x-(2y-z)\\
&=&2(2x-y)-(2x-z)\\
&=&s_{s_{x}(y)}\circ s_{x}(z)
\end{eqnarray}
$S^{n}\coloneqq\{x\in\mathbb{R}^{n+1}|< x,x>=1\}$は、$s_{x}(y)=2< y,x>x-y$と定める事で対称空間になる。
[S1]$s_{x}(x)=2< x,x>x-x=x$
[S2]
\begin{eqnarray}
s_{x}^{2}(y)&=&2< s_{x}(y),x>x-s_{x}(y)\\
&=&2<2< y,x>x-y,x>x-(2< y,x>x-y)\\
&=&4< y,x>x-2< y,x>x-2< y,x>x+y\\
&=&y
\end{eqnarray}
[S3]
\begin{eqnarray}
s_{x}\circ s_{y}(z)&=&2< s_{y}(z),x>x-s_{y}(z)\\
&=&2<2< z,y>y-z,x>x-(2< z,y>y-z)\\
&=&4< y,x>< z,y>x-2< z,x>x-2< z,y>y+z
\end{eqnarray}
\begin{eqnarray}
s_{s_{x}(y)}\circ s_{x}(z)&=&2< s_{x}(z),s_{x}(y)>s_{x}(y)-s_{x}(z)\\
&=&2<2< z,x>x-z,2< y,x>x-y>(2< y,x>x-y)-(2< z,x>x-z)\\
&=&2< z,y>(2< y,x>x-y)-(2< z,x>x-z)\\
&=&4< y,x>< z,y>x-2< z,x>x-2< z,y>y+z
\end{eqnarray}
例3において$s_{x}\in O(n+1)$である事を示せ。
\begin{eqnarray} < s_{x}(y),s_{x}(z)>&=&<2< y,x>x-y,2< z,x>x-z>\\ &=&4< y,x>< z,x>-2< y,x>< z,x>-2< y,x>< z,x>+< y,z>\\ &=&< y,z> \end{eqnarray}
$X=\{1,2,3,4\}$とし次の様に$s$を定めるとカンドルになる事を証明せよ。
\begin{eqnarray}
\left\{
\begin{array}{l}
s_{1}=(234)\\
s_{2}=(143)\\
s_{3}=(124)\\
s_{4}=(132)
\end{array}
\right.
\end{eqnarray}
[$S1$]$s$の定義より、$s_{1},s_{2},s_{3},s_{4}$は$1,2,3,4$をそれぞれ動かさないので(S1)の性質を満たす。
[$S2^{'}$]$s_{1},s_{2},s_{3},s_{4}$は全単射なのでこれも正しい。
[$S3$]
| $s_{1}$ | $s_{2}$ | $s_{3}$ | $s_{4}$ | |
|---|---|---|---|---|
| $s_{1}$ | $(2,4,3)$ | $(1,2,3)$ | $(1,3,4)$ | $(1,4,2)$ |
| $s_{2}$ | $(1,4,2)$ | $(1,3,4)$ | $(1,2,3)$ | $(2,4,3)$ |
| $s_{3}$ | $(1,2,3)$ | $(2,4,3)$ | $(1,4,2)$ | $(1,3,4)$ |
| $s_{4}$ | $(1,3,4)$ | $(1,4,2)$ | $(2,4,3)$ | $(1,2,3)$ |
| $s_{1}$ | |
|---|---|
| $s_{1}$ | $(2,4,3)$ |
| $s_{3}$ | $(1,2,3)$ |
| $s_{4}$ | $(1,3,4)$ |
| $s_{2}$ | $(1,4,2)$ |
| $s_{2}$ | |
|---|---|
| $s_{4}$ | $(1,4,2)$ |
| $s_{2}$ | $(1,3,4)$ |
| $s_{1}$ | $(1,2,3)$ |
| $s_{3}$ | $(2,4,3)$ |
| $s_{3}$ | |
|---|---|
| $s_{2}$ | $(1,2,3)$ |
| $s_{4}$ | $(2,4,3)$ |
| $s_{3}$ | $(1,4,2)$ |
| $s_{1}$ | $(1,3,4)$ |
| $s_{4}$ | |
|---|---|
| $s_{3}$ | $(1,3,4)$ |
| $s_{1}$ | $(1,4,2)$ |
| $s_{2}$ | $(2,4,3)$ |
| $s_{4}$ | $(1,2,3)$ |
$G$を群、$M$を集合とする。この時写像$\Phi:G\times M\rightarrow M$を次の様に書く:$g\cdot p\coloneqq \Phi(g,p)$。この写像$\Phi$が群作用であるとは下記の性質を持つ場合を言う。
- $\forall g,h\in G:\forall p\in M:(gh)\cdot p=g\cdot(h\cdot p)$
- $\exists e\in G\ s.t.\ \forall p\in M:e\cdot p = p$
$GL(n,\mathbb{R})\times \mathbb{R}^{n}\ni(g,v)\mapsto gv\in\mathbb{R}^{n}$は群作用
$G_{k}(\mathbb{R}^{n})\coloneqq\{V\subset\mathbb{R}^{n}|Vはk次元線形部分空間\}$を実グラスマン多様体と呼ぶ。
このグラスマン多様体には次の様な群作用を定義できる。$GL(n,\mathbb{R})\times G_{k}(\mathbb{R}^{n})\ni(g,V)\mapsto g\cdot V\in G_{k}(\mathbb{R}^{n})$
$\mathbb{R}H^{2}\coloneqq \{z\in\mathbb{C}|Im(z)\gt 0\}$を上半面と呼ぶ。この時、$SL(2,\mathbb{R})\curvearrowright \mathbb{R}H^{2}$を次の様に定義する。
\begin{equation}
\begin{pmatrix}
a&b\\c&d
\end{pmatrix}\cdot z=\frac{az+b}{cz+d}
\end{equation}
すると、実際、群作用になる。
[1]
\begin{eqnarray}
(\begin{pmatrix}a&b\\c&d\end{pmatrix}\begin{pmatrix}e&f\\g&h\end{pmatrix})\cdot z&=&\begin{pmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{pmatrix}\cdot z\\
&=&\frac{(ae+bg)z+af+bh}{(ce+dg)z+cf+dh}\\
&=&\frac{a\frac{ez+f}{gz+h}+b}{c\frac{gz+h}{gz+h}+d}\\
&=&\begin{pmatrix}a&b\\c&d\end{pmatrix}\cdot(\begin{pmatrix}e&f\\g&h\end{pmatrix}\cdot z)
\end{eqnarray}
[2]$e=\begin{pmatrix}1&0\\0&1\end{pmatrix}$
$G$を群、$M$を集合とする。この時、群作用$G\curvearrowright M$が推移的であるとは次の条件が成り立つ事を言う。
\begin{equation}
\forall p,q\in M:\exists g\in G\ s.t. g\cdot p=q
\end{equation}
また、$M$は$G$に関して等質であると言う。
$r\in M$を固定する。この時、群$G$の$M$への作用が推移的である事は次の条件と同値。
\begin{equation}
\forall q\in M:\exists g\in G\ s.t. g\cdot r=q
\end{equation}
[$\Rightarrow$]$\forall q\in M:\exists g\in G\ s.t. g\cdot r=q$が成り立つとする。
すると下記の様に計算できるので、群$G$の$M$への作用は推移的。
\begin{eqnarray}
\forall p,q\in M:\exists g_{p},g_{q}\in G\ s.t.\left\{
\begin{array}{l}
g_{p}r=p\\
g_{q}r=q
\end{array}
\right.
\end{eqnarray}
\begin{equation}
(g_{q}g_{p}^{-1})\cdot p=q
\end{equation}
[$\Leftarrow$]群$G$の$M$への作用が推移的であるとすると。$r=p$とすれば証明完了。
$n\in\mathbb{N}(n\geq 1)$に対して$O(n+1)\curvearrowright S^{n}$は推移的。
[1]
\begin{eqnarray}
\forall x\in S^{n}:< x,x>=1
\end{eqnarray}
[2]また$\forall y\in S^{n}:\exists A\in GL(n,\mathbb{R})\ s.t.\ Ax=y$が成り立ちなおかつ、
\begin{eqnarray}
< y,y>&=&< Ax,Ax>\\
&=&(Ax)^{t}(Ax)\\
&=&x^{t}A^{t}Ax\\
&=&< x,x>\\
&=&1
\end{eqnarray}
ゆえに$A^{t}A=E_{n+1}$が得られるので$A\in O(n+1)$
つまり、$O(n+1)\curvearrowright S^{n}$は推移的。
$G$を群とし、$K$をその部分群とする。
この時、次の様な同値関係を導入する。$g\sim h\overset{def}\Leftrightarrow g^{-1}h\in K$
また$g\in G$を含む同値類を$[g]=gK\coloneqq\{gk|k\in K\}$の様に定める。
上記の同値類は$[g]=\{h|g\sim h,h\in G\}$と同じ。
\begin{eqnarray} g\sim h&\Leftrightarrow&g^{-1}h\in K\\ &\Leftrightarrow&\exists k\in K\ s.t.\ g^{-1}h=k\\ &\Leftrightarrow&h=gk\in gK \end{eqnarray}
群$G$を部分群$K$による同値関係で割った商集合を$G/K$と書き剰余集合と言う。
$K$を群$G$の任意の部分群とする。この時、$G/K$は$G$に関して等質。
ただし$G$による$G/K$への作用は次の様に定める$g\cdot [h]\coloneqq [gh]$
$h\in G$を固定する。そして$G$は群なので以下の式が成り立つ。
\begin{equation}
\forall l\in G:\exists g\in G\ s.t.\ l=gh
\end{equation}
ゆえに、$[h]\in G/K$を固定すると$\forall [l]\in G/K:\exists G\ s.t.\ [l]=g\cdot [h]$が得られる。
この計算がwell-definedである事も次の様にして確認できる。
\begin{eqnarray}
\left\{
\begin{array}{l}
h\sim h^{'}\Leftrightarrow\exists k_{h}\in K\ s.t.\ h=h^{'}k_{h}\\
l\sim l^{'}\Leftrightarrow\exists k_{l}\in K\ s.t.\ l=l^{'}k_{l}
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
[l^{'}]\ni l^{'}k_{l}=gh^{'}k_{h}\Leftrightarrow l^{'}=gh^{'}k_{h}k_{l}^{-1}\in[gh^{'}]
\end{eqnarray}
$M$が$G$に関して等質であるとする。この時、$p\in M$に対して次の様な写像$\varphi:G/G_{p}\ni [g]\mapsto g\cdot p\in M$は全単射になる。
ただし、$G_{p}\coloneqq \{g\in G|g\cdot p=p\}$
[1]全射性の証明
$M$は等質なので$\forall q\in M$に対して$\exists g\in G\ s.t.\ g\cdot p=q$が成り立つ。
ゆえに、全射性は示せた。
[2]単射性の証明
\begin{eqnarray}
\exists [g_{1}],[g_{2}]\in G/G_{p}\ s.t.\ g_{1}\cdot p=g_{2}\cdot p
\end{eqnarray}
が成り立ったとする。
すると
\begin{eqnarray}
p&=&g_{2}^{-1}\cdot(g_{1}\cdot p)\\
&=&(g_{2}^{-1}g_{1})\cdot p
\end{eqnarray}
が成り立つので、$[g_{2}^{-1}g_{1}]=[1]$が得られるので$[g_{1}]=[g_{2}]$。
つまり、単射性も証明された。
集合$M$が$G$に関して等質である事と$M=G/K$は同値
$K=G_{p}$とすればよい。
$n\in\mathbb{N}(n\geq 1)$とする。この時、球面$S^{n}$は以下の様な等質空間表示を持つ。
\begin{eqnarray}
S^{n}\coloneqq O(n+1)/\{\begin{pmatrix}1&O_{1,n}\\O_{n,1}&A\end{pmatrix}|A\in O(n)\}
\end{eqnarray}
Lie代数
$\mathfrak{g}$を実線形空間とし$[,]:\mathfrak{g}\times\mathfrak{g}\rightarrow\mathfrak{g}$を双線形写像とする。この時、$(\mathfrak{g},[,])$がLie代数であるとは次の条件が成り立つ事である。
- $\forall X,Y\in\mathfrak{g}:[X,Y]=-[Y,X]$
- $\forall X,Y,Z\in\mathfrak{g}:[[X,Y],Z]+[[Y,Z],Z]+[[Z,X],Y]=0$
$\mathfrak{gl}(n,\mathbb{R})\coloneqq M(n,\mathbb{R})$は次の様な括弧積によってLie代数になる。
\begin{equation}
\forall X,Y\in M(n,\mathbb{R}):[X,Y]\coloneqq XY-YX
\end{equation}
[1]
\begin{eqnarray}
[X,Y]&=&XY-YX\\
&=&-(YX-XY)\\
&=&-[Y,X]
\end{eqnarray}
[2]
\begin{eqnarray}
[[X,Y],Z]+[[Y,Z],Z]+[[Z,X],Y]&=&[XY-YX,Z]+[YZ-ZY,X]+[ZX-XZ,Y]\\
&=&(XY-YX)Z-Z(XY-YX)+(YZ-ZY)X-X(YZ-ZY)+(ZX-XZ)Y-Y(ZX-XZ)\\
&=&\underbrace{XYZ}_{1}-\underbrace{YXZ}_{2}-\underbrace{ZXY}_{3}+\underbrace{ZYX}_{4}+\underbrace{YZX}_{5}-\underbrace{ZYX}_{4}-\underbrace{XYZ}_{1}+\underbrace{XZY}_{6}+\underbrace{ZXY}_{3}-\underbrace{XZY}_{6}-\underbrace{YZX}_{5}+\underbrace{YXZ}_{2}\\
&=&0
\end{eqnarray}
$\mathfrak{g}$をLie代数とする。この時$\mathfrak{g}^{'}\subset\mathfrak{g}$がLie部分代数であるとは次の条件が成り立つ事を言う。
- $\mathfrak{g}^{'}$は$\mathfrak{g}$内の線形部分空間
- $\forall X,Y\in\mathfrak{g}^{'}:[X,Y]\in\mathfrak{g}^{'}$
下記の集合は$\mathfrak{gl}(n,\mathbb{R})$のLie部分代数
$\mathfrak{sl}(n,\mathbb{R})\coloneqq\{X\in\mathfrak{gl}(n,\mathbb{R})|tr(X)=0\}$
[1]まず$\mathfrak{g}^{'}$は$\mathfrak{g}$内の線形部分空間である事は以下の計算により示せる。
\begin{eqnarray}
\forall X,Y\in\mathfrak{g}^{'}:\alpha,\beta\in\mathbb{R}:tr(\alpha X+\beta Y)&=&\alpha tr(X)+\beta tr(Y)\\
&=&\alpha 0+\beta 0\\
&=&0
\end{eqnarray}
[2]$\forall X,Y\in\mathfrak{g}^{'}:[X,Y]\in\mathfrak{g}^{'}$について定義に従って計算すれば良い。
\begin{eqnarray}
tr([X,Y])&=&tr(XY-YX)\\
&=&tr(XY)-tr(YX)\\
&=&tr(XY)-tr(XY)\\
&=&0
\end{eqnarray}
Lie代数$\mathfrak{g}$が線形空間としての直和分解$\mathfrak{g}=\bigoplus_{k\in\mathbb{Z}}\mathfrak{g}^{k}$が階別Lie代数であるとは次の条件を満たす時を言う。
\begin{equation}
\forall p,q\in\mathbb{Z}:[\mathfrak{g}^{p},\mathfrak{g}^{q}]\subset\mathfrak{g}^{p+q}
\end{equation}
階別Lie代数$\mathfrak{g}=\bigoplus_{k\in\mathbb{Z}}\mathfrak{g}^{k}$が第$r$種であるとは下記の条件を満たす事を言う。
- $\mathfrak{g}^{r}\neq 0$
- $|p|\gt r\Rightarrow \mathfrak{g}^{p}=0$
$\mathfrak{sl}(3,\mathbb{R})$に対して、次の様な階別Lie代数を考えるとこれは第1種のLie代数となる。
\begin{eqnarray}
\left\{
\begin{array}{l}
\mathfrak{g}^{-1}\coloneqq\{\left(\begin{array}{@{}c|c@{}}\begin{matrix}0\end{matrix}&O_{1,2}\\ \hline\vb*{a}&O_{2,2}\end{array}\right)|\vb*{a}\in\mathbb{R}^{2}\}\\
\mathfrak{g}^{0}\coloneqq\{\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)|a,d,e,f\in\mathbb{R},a+d+f=0\}\\
\mathfrak{g}^{1}\coloneqq\{\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)|\vb*{b}\in\mathbb{R}^{2}\}
\end{array}
\right.
\end{eqnarray}
[1]まず階別Lie代数である事を確認
\begin{eqnarray}
\left(\begin{array}{@{}c|c@{}}\begin{matrix}0\end{matrix}&O_{1,2}\\ \hline\vb*{a}&O_{2,2}\end{array}\right)\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)-\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)\left(\begin{array}{@{}c|c@{}}\begin{matrix}0\end{matrix}&O_{1,2}\\ \hline\vb*{a}&O_{2,2}\end{array}\right)=\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{a}a+\begin{pmatrix}d&e\\e&f\end{pmatrix}\vb*{a}&O_{2,2}\end{array}\right)\in\mathfrak{g}^{-1}
\end{eqnarray}
\begin{eqnarray}
\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{a}&O_{2,2}\end{array}\right)\left(\begin{array}{@c{}|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)-\left(\begin{array}{@c{}|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)
\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{a}&O_{2,2}\end{array}\right)=\left(\begin{array}{@c{}|c@{}}\vb*{b}^{t}\vb*{a}&O_{1,2}\\\hline O_{2,1}&\vb*{a}\vb*{b}^{t}\end{array}\right)\in\mathfrak{g}^{0}\\
\end{eqnarray}
\begin{eqnarray}
\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)\left(\begin{array}{@{}c|c@{}}\begin{matrix}p\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}q&s\\s&r\end{matrix}\end{array}\right)-\left(\begin{array}{@{}c|c@{}}\begin{matrix}p\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}q&s\\s&r\end{matrix}\end{array}\right)\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)=\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline O_{2,1}&\begin{pmatrix}d&e\\e&f\end{pmatrix}\begin{pmatrix}q&s\\s&r\end{pmatrix}-\begin{pmatrix}q&s\\s&r\end{pmatrix}\begin{pmatrix}d&e\\e&f\end{pmatrix}\end{array}\right)\in \mathfrak{g}^{0}
\end{eqnarray}
\begin{eqnarray}
\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)-\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)
\left(\begin{array}{@{}c|c@{}}\begin{matrix}a\end{matrix}&O_{1,2}\\\hline O_{2,1}&\begin{matrix}d&e\\e&f\end{matrix}\end{array}\right)=\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\begin{pmatrix}d&e\\e&f\end{pmatrix}\\\hline O_{2,1}&O_{2,2}\end{array}\right)\in\mathfrak{g}^{1}
\end{eqnarray}
[2]$\mathfrak{g}=\mathfrak{g}^{-1}\oplus\mathfrak{g}^{0}\oplus\mathfrak{g}^{1}\oplus\{0\}$であり
\begin{eqnarray}
\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{a}&O_{2,2}\end{array}\right)
\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{b}&O_{2,2}\end{array}\right)-
\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{b}&O_{2,2}\end{array}\right)
\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline \vb*{a}&O_{2,2}\end{array}\right)=\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\O_{2,1}&O_{2,2}\end{array}\right)=O
\end{eqnarray}
\begin{eqnarray}
\left(\begin{array}{@{}c|c@{}}0&\vb*{a}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)
\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)-
\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)
\left(\begin{array}{@{}c|c@{}}0&\vb*{a}^{t}\\\hline O_{2,1}&O_{2,2}\end{array}\right)=\left(\begin{array}{@{}c|c@{}}0&O_{1,2}\\\hline O_{2,1}&O_{2,2}\end{array}\right)=O
\end{eqnarray}
なので第1種のLie代数
Lie代数$\mathfrak{g}$に対して次の様な写像$\forall X\in\mathfrak{g}:ad_{X}:\mathfrak{g}\ni Y\mapsto [X,Y]\in\mathfrak{g}$と定める。これを随伴写像と呼ぶ。
$ad_{X}$は線形写像
[1]
\begin{eqnarray}
\forall Y,Z\in\mathfrak{g}:ad_{X}(Y+Z)&=&[X,Y+Z]\\
&=&[X,Y]+[X,Z]\\
&=&ad_{X}(Y)+ad_{X}(Z)
\end{eqnarray}
[2]
\begin{eqnarray}
\forall c\in\mathbb{R}:\forall Y\in\mathfrak{g}:ad_{X}(cY)&=&[X,cY]\\
&=&c[X,Y]\\
&=&cad_{X}(Y)
\end{eqnarray}
$Z\in\mathfrak{g}$に対して、$ad_{Z}$が対角化可能であり、すべての固有値が整数であるとする。
この時、次の様にして階別Lie代数が得られる。
\begin{eqnarray}
\left\{
\begin{array}{l}
\mathfrak{g}=\bigoplus_{k\in\mathbb{Z}}\mathfrak{g}^{k}\\
\mathfrak{g}^{k}\coloneqq\{X\in\mathfrak{g}|ad_{Z}(X)=kX\}\\
\end{array}
\right.
\end{eqnarray}
なお、$Z\in\mathfrak{g}$を階別Lie代数の特性元と言う。
[1]まず異なる整数$k,l\in\mathbb{Z}$に対して$\mathfrak{g}^{k}\cap\mathfrak{g}^{l}=\{0\}$である事を示す。
実際、$X\in\mathfrak{g}^{k}\cap\mathfrak{g}^{l}$とすると以下の式が成り立つ。
\begin{eqnarray}
ad_{Z}(X)&=&kX\\
&=&lX
\end{eqnarray}
ゆえに$(k-l)X=0$であり、$k-l\neq 0$なので$X=0$を得る。
[2]以下$N=\dim{\mathfrak{g}}$とおく。$ad_{Z}$は対角化可能なので、その表現行列を$A$とするとある正則行列$P\in GL(N,\mathbb{R})$が存在し次式が成り立つ。
\begin{equation}
P^{-1}AP=diag(\underbrace{k_{1},k_{1},...,k_{1}}_{m_{1}個},...,\underbrace{k_{l},k_{l},...,k_{l}}_{m_{l}個})
\end{equation}
また$P$は正則なので、$X_{1},...,X_{N}\in \mathfrak{g}$が存在して$P=\begin{pmatrix}X_{1}&\cdots& X_{N}\end{pmatrix}$が成り立つ。
この事から、
\begin{eqnarray}
AP&=&\begin{pmatrix}AX_{1}&\cdots& AX_{N}\end{pmatrix}\\
&=&\begin{pmatrix}d_{1}X_{1}&\cdots&d_{N}X_{N}\end{pmatrix}\\
&=&Pdiag(\underbrace{k_{1},k_{1},...,k_{1}}_{m_{1}個},...,\underbrace{k_{l},k_{l},...,k_{l}}_{m_{l}個})
\end{eqnarray}
また、$X_{i1},X_{i2},...,X_{im_{i}}$は仮定より一次独立なので、$dim(\mathfrak{g}^{k_{1}})\geq m_{k}$。さらに次の様な不等式が得られる。$m_{1}+m_{2}+\cdots+m_{l}=N\leq dim(\mathfrak{g}^{k_{1}})+dim(\mathfrak{g}^{k_{2}})+\cdots+dim(\mathfrak{g}^{k_{l}})\leq N$
ゆえに、
\begin{equation}
\mathfrak{g}=\mathfrak{g}^{k_{1}}\oplus\mathfrak{g}^{k_{2}}\oplus\cdots\oplus\mathfrak{g}^{k_{l}}
\end{equation}
$\mathfrak{g}=\mathfrak{sl}(2,\mathbb{R})$に対して次の様な行列は特性元である事を示してください。
\begin{equation}
Z\coloneqq\frac{1}{2}\begin{pmatrix}1&0\\0&-1\end{pmatrix}
\end{equation}
[1]$X=\begin{pmatrix}a&b\\c&-a\end{pmatrix}\in\mathfrak{sl}(2,\mathbb{R})$とすると下記の様な計算が出来る。
\begin{eqnarray}
ad_{Z}(X)&=&[Z,X]\\
&=&ZX-XZ\\
&=&\begin{pmatrix}0&b\\-c&0\end{pmatrix}\\
&=&\lambda\begin{pmatrix}a&b\\c&-a\end{pmatrix}
\end{eqnarray}
[2]
$\lambda=0$の場合の固有ベクトルは$\begin{pmatrix}a&0\\0&-a\end{pmatrix}$
$\lambda=1$の場合の固有ベクトルは$\begin{pmatrix}0&b\\0&0\end{pmatrix}$
$\lambda=-1$の場合の固有ベクトルは$\begin{pmatrix}0&0\\c&0\end{pmatrix}$
$\mathfrak{g}=\mathfrak{sl}(3,\mathbb{R})$に対して、次の元は特性元を成す事を証明してください。
\begin{equation}
H^{1}\coloneqq\frac{1}{3}\begin{pmatrix}2&0&0\\0&-1&0\\0&0&-1\end{pmatrix}
\end{equation}
[1]$X=\begin{pmatrix}a&c&d\\e&b&f\\g&h&-a-b\end{pmatrix}$とすると
\begin{eqnarray}
ad_{H^{1}}(X)&=&[H^{1},X]\\
&=&\frac{1}{3}\begin{pmatrix}2&0&0\\0&-1&0\\0&0&-1\end{pmatrix}\begin{pmatrix}2&0&0\\0&-1&0\\0&0&-1\end{pmatrix}-\begin{pmatrix}2&0&0\\0&-1&0\\0&0&-1\end{pmatrix}\frac{1}{3}\begin{pmatrix}2&0&0\\0&-1&0\\0&0&-1\end{pmatrix}\\
&=&\begin{pmatrix}
0&c&d\\-e&0&0\\-g&0&0
\end{pmatrix}\\
&=&\lambda\begin{pmatrix}a&c&d\\e&b&f\\g&h&-a-b\end{pmatrix}
\end{eqnarray}
[2]
$\lambda=0$の場合の固有ベクトルは$\begin{pmatrix}a&0&0\\0&b&f\\0&h&-a-b\end{pmatrix}$
$\lambda=1$の場合の固有ベクトルは$\begin{pmatrix}0&c&d\\0&0&0\\0&0&0\end{pmatrix}$
$\lambda=-1$の場合の固有ベクトルは$\begin{pmatrix}0&0&0\\e&0&0\\g&0&0\end{pmatrix}$
となる事が分かる。
Lie代数$\mathfrak{sl}(n,\mathbb{R})$次の様な行列は特性元である事を示してください。
\begin{equation}
Z=\frac{1}{n}diag(n-1,\underbrace{-1,-1,...,-1}_{n-1個})
\end{equation}
[1]$X=\left(\begin{array}{@{}c|c@{}}x_{11}&\vb*{y}^{t}\\\hline \vb*{z}&\tilde{X}\end{array}\right)\quad(tr(X)=x_{11}+tr(\tilde{X})=0)$とすると
\begin{eqnarray}
ad_{Z}(X)&=&[Z,X]\\
&=&\left(\begin{array}{@{}c|c@{}}0&\begin{matrix}x_{12}&\cdots x_{1n}\end{matrix}\\\hline \begin{matrix}-x_{21}\\-x_{31}\\\vdots\\-x_{n1}\end{matrix}&O_{n-1,n-1}\end{array}\right)\\
&=&\lambda X
\end{eqnarray}
[2]
$\lambda=0$の場合の固有ベクトルは$\left(\begin{array}{@{}c|c@{}}x_{11}&O_{1,n-1}\\\hline O_{1,n-1}&\tilde{X}\end{array}\right)$
$\lambda=1$の場合の固有ベクトルは$\left(\begin{array}{@{}c|c@{}}0&\vb*{y}^{t}\\\hline O_{1,n-1}&O_{n-1,n-1}\end{array}\right)$
$\lambda=1$の場合の固有ベクトルは$\left(\begin{array}{@{}c|c@{}}0&O_{1,n-1}\\\hline \vb*{z}&O_{n-1,n-1}\end{array}\right)$
$\mathfrak{g}^{'}\subset\mathfrak{g}$内のイデアルであるとは次の式が成り立つ事を言う。
- $\mathfrak{g}^{'}$が$\mathfrak{g}$内の線形部分空間
- $\forall X\in\mathfrak{g},\forall Y\in\mathfrak{g}^{'}:[X,Y]\in\mathfrak{g}^{'}$
$\mathfrak{sl}(n,\mathbb{R})\subset\mathfrak{gl}(n,\mathbb{R})$はイデアル。
[1]これは証明済みなので省略
[2]
\begin{eqnarray}
\forall X\in \mathfrak{gl}(n,\mathbb{R}):\forall Y\in\mathfrak{sl}(n,\mathbb{R}):tr([X,Y])&=&tr(XY-YX)\\
&=&tr(XY)-tr(YX)\\
&=&tr(XY)-tr(XY)\\
&=&0
\end{eqnarray}
$\mathfrak{g}$が単純であるとは、$dim{\mathfrak{g}}\gt 1$であり、なおかつ自明なイデアル($\{0\},\mathfrak{g}$)以外を持たない事を言う。
$n\in\mathbb{N}(n\geq 3)$に対して$\mathfrak{sl}(n,\mathbb{R})$は単純Lie代数
[0]
\begin{eqnarray}
[E_{pq},E_{rs}]&=&[(\delta_{pi}\delta_{qj}),(\delta_{ri}\delta_{sj})]\\
&=&(\sum_{j}\delta_{pi}\delta_{qj}\delta_{rj}\delta_{sk}-\sum_{j}\delta_{ri}\delta_{sj}\delta_{pj}\delta_{qk})_{ik}\\
&=&(\delta_{qr}\delta_{pi}\delta_{sk}-\delta_{sp}\delta_{ri}\delta_{qk})_{ik}\\
&=&\delta_{qr}E_{ps}-\delta_{ps}E_{rq}
\end{eqnarray}
特に
[1]$\mathfrak{sl}(n,\mathbb{R})=span\{E_{ij}|i\neq j\}\oplus span\{E_{ii}-E_{i+1i+1}|i=1,2,...,n-1\}$である事を用いる。
[2]$(\{0\},\mathfrak{sl}(n,\mathbb{R})\neq)\mathfrak{J}\subset\mathfrak{sl}(n,\mathbb{R})$がイデアルであるとする。
そして$0\neq X\in\mathfrak{J}$を一つ取る。
[3]$X=\sum_{i,j}X_{ij}E_{ij}\in\mathfrak{J}$の様に書く。
\begin{eqnarray}
[E_{pq},X]&=&\sum_{i,j}X_{ij}[E_{pq},E_{ij}]\\
&=&\sum_{i,j}X_{ij}(\delta_{iq}E_{pj}-\delta_{jp}E_{iq})\\
&=&\sum_{j}X_{qj}E_{pj}-\sum_{i}X_{ip}E_{iq}\\
&=&(X_{qq}-X_{pp})E_{pq}+\sum_{j\neq q}X_{qj}E_{pj}-\sum_{i\neq p}X_{ip}E_{iq}
\end{eqnarray}
特に$X_{pp}\neq X_{qq}$また、$X_{ij}=0\quad(i\neq j)$とすれば$E_{pq}\in\mathfrak{J}$となる事が分かる。
また$X_{pp}=X_{qq}$また$X_{pq}=X_{qp}=1$他は$X_{ij}=0\quad(otherwise)$すると$E_{pp}-E_{qq}\in\mathfrak{J}$が得られる。
[4]また
\begin{eqnarray}
E_{pp}-E_{qq}&=&(E_{pp}-E_{p+1p+1})+(E_{p+1p+1}-E_{p+2p+2})+\cdots+(E_{q-1q-1}-E_{qq})
\end{eqnarray}
なので$E_{ii}-E_{i+1i+1}\in\mathfrak{J}$が得られる。
[5]以上をまとめると$\mathfrak{J}=span\{E_{ij}|i\neq j\}\oplus span\{E_{ii}-E_{i+1i+1}|i=1,2,...,n-1\}\oplus \mathfrak{R}\subset\mathfrak{sl}(n,\mathbb{R})$なので$\mathfrak{R}=\{0\}$がすぐに分かるので$\mathfrak{J}=\mathfrak{sl}(n,\mathbb{R})$
ゆえに、$\mathfrak{sl}(n,\mathbb{R})$は単純なLie代数。
Lie代数$\mathfrak{g}$が半単純であるとは単純Lie代数の直和として書ける事を言う。
次の様な写像$B:\mathfrak{g}\times\mathfrak{g}\rightarrow\mathbb{R}$をKilling形式と言う。
\begin{equation}
B(X,Y)=tr(ad_{X}\circ ad_{Y})
\end{equation}
Killing形式$B$は双線形写像であり次式を満たす。
\begin{equation}
\forall X,Y,Z\in \mathfrak{g}:B([X,Y],Z)+B(Y,[X,Z])=0
\end{equation}
[0]
\begin{eqnarray}
\forall X,Y,Z\in\mathfrak{g}:ad_{X}\circ ad_{Y}(Z)&=&[X,[Y,Z]]\\
&=&-[Y,[Z,X]]-[Z,[X,Y]]\\
&=&[Y,[X,Z]]+[[X,Y],Z]\\
&=&ad_{Y}\circ ad_{X}(Z)+ad_{[X,Y]}(Z)
\end{eqnarray}
[1]後半部分から証明する。
\begin{eqnarray}
B([X,Y],Z)+B(Y,[X,Z])&=&tr(ad_{[X,Y]}\circ ad_{Z})+tr(ad_{Y}\circ ad_{[X,Z]})\\
&=&tr((ad_{X}\circ ad_{Y}-ad_{Y}\circ ad_{X})\circ ad_{Z})+tr(ad_{Y}\circ(ad_{X}\circ ad_{Z}-ad_{Z}\circ ad_{X}))\\
&=&tr(ad_{X}\circ ad_{Y}\circ ad_{Z})-tr(ad_{Y}\circ ad_{X}\circ ad_{Z})+tr(ad_{Y}\circ ad_{X}\circ ad_{Z})-tr(ad_{Y}\circ ad_{Z}\circ ad_{X})\\
&=&tr(ad_{X}\circ ad_{Y}\circ ad_{Z})-tr(ad_{Y}\circ ad_{Z}\circ ad_{X})\\
&=&tr(ad_{X}\circ ad_{Y}\circ ad_{Z})-tr(ad_{X}\circ ad_{Y}\circ ad_{Z})\\
&=&0
\end{eqnarray}
一般線形Lie代数$\mathfrak{gl}(n,\mathbb{R})$のkilling形式$B$は次の様になる。
\begin{equation}
B(X,Y)=2ntr(XY)-2tr(X)tr(Y)
\end{equation}
[0]$[E_{pq},E_{rs}]=\delta_{qr}E_{ps}-\delta_{ps}E_{rq}$を用いる。
[1]$X=\sum_{i,j}x_{ij}E_{ij},Y=\sum_{i,j}y_{ij}E_{ij},Z_{ij}=\sum_{i,j}z_{ij}E_{ij}\in \mathfrak{gl}(n,\mathbb{R})$の様に置く。
すると
\begin{eqnarray}
ad_{X}\circ ad_{Y}(Z)&=&[X,[Y,Z]]\\
&=&\sum_{p,q,r,s,t,u}x_{pq}y_{rs}z_{tu}[E_{pq},[E_{rs},E_{tu}]]\\
&=&\sum_{p,q,r,s,t,u}x_{pq}y_{rs}z_{tu}[E_{pq},\delta_{st}E_{ru}-\delta_{ru}E_{ts}]\\
&=&\sum_{p,q,r,s,u}x_{pq}y_{rs}z_{su}[E_{pq},E_{ru}]-\sum_{p,q,r,s,t}x_{pq}y_{rs}z_{tr}[E_{pq},E_{ts}]\\
&=&\sum_{p,q,r,s,u}x_{pq}y_{rs}z_{su}(\delta_{qr}E_{pu}-\delta_{pu}E_{rq})-\sum_{p,q,r,s,t}x_{pq}y_{rs}z_{tr}(\delta_{qt}E_{ps}-\delta_{ps}E_{tq})\\
&=&\sum_{p,q,s,u}x_{pq}y_{qs}z_{su}E_{pu}-\sum_{p,q,r,s}x_{pq}y_{rs}z_{sp}E_{rq}-\sum_{p,q,r,s}x_{pq}y_{rs}z_{qr}E_{ps}+\sum_{p,q,r,t}x_{pq}y_{rp}z_{tr}E_{tq}
\end{eqnarray}
特に$z=E_{ij}$として
\begin{eqnarray}
ad_{X}\circ ad_{Y}(E_{ij})&=&\sum_{p,q,s,u}x_{pq}y_{qs}\delta_{si}\delta_{uj}E_{pu}-\sum_{p,q,r,s}x_{pq}y_{rs}\delta_{si}\delta_{pj}E_{rq}-\sum_{p,q,r,s}x_{pq}y_{rs}\delta_{qi}\delta_{rj}E_{ps}+\sum_{p,q,r,t}x_{pq}y_{rp}\delta_{ti}\delta_{rj}E_{tq}\\
&=&\sum_{p,q}x_{pq}y_{qi}E_{pj}-\sum_{q,r}x_{jq}y_{ri}E_{rq}-\sum_{p,s}x_{pi}y_{js}E_{ps}+\sum_{p,q}x_{pq}y_{jp}E_{iq}
\end{eqnarray}
さらに両辺のトレースを取って
\begin{eqnarray}
tr(ad_{X}\circ ad_{Y})&=&\sum_{i,j}< E_{ij}|ad_{X}\circ ad_{Y}(E_{ij})>\\
&=&\sum_{i,j,p,q}< E_{ij}|x_{pq}y_{qi}E_{pj}>-\sum_{i,j,q,r}< E_{ij}|x_{jq}y_{ri}E_{rq}>-\sum_{i,j,p,s}< E_{ij}|x_{pi}y_{js}E_{ps}>+\sum_{i,j,p,q}< E_{ij}|x_{pq}y_{jp}E_{iq}>\\
&=&\sum_{j,p,q}x_{pq}y_{qp}-\sum_{q,r}x_{qq}y_{rr}-\sum_{p,s}x_{pp}y_{ss}+\sum_{i,p,q}x_{pq}y_{qp}\\
&=&2n\sum_{p,q}x_{pq}y_{qp}-2\sum_{q,r}x_{qq}y_{rr}\\
&=&2ntr(XY)-2tr(X)tr(Y)
\end{eqnarray}
Lie代数$\mathfrak{g}$のイデアルを$\mathfrak{g}^{'}$とし、それぞれのKilling形式を$B,B^{'}$とする。この時、$B^{'}$は$B$の制限となる。
つまり
\begin{equation}
B^{'}=B|_{\mathfrak{g}^{'}\times\mathfrak{g}^{'}}
\end{equation}
イデアル$\mathfrak{g}^{'}$を張る基底を$\{E_{ij}\}$の様に置くと、killing形式$B^{'}$は定義より
\begin{eqnarray}
\forall X,Y\in\mathfrak{g}^{'}:B(X,Y)&=&\sum_{i,j}< E_{ij}|ad_{X}\circ ad_{Y})E_{ij}>
\end{eqnarray}
なので$B^{'}=B|_{\mathfrak{g}^{'}\times\mathfrak{g}^{'}}$
$\mathfrak{sl}(n,\mathbb{R})$のkilling形式は下記の様に書ける。
\begin{eqnarray}
B(X,Y)=2ntr(XY)
\end{eqnarray}
$tr(X)=tr(Y)=0$なので$B^{'}(X,Y)=B|_{\mathfrak{g}^{'}\times \mathfrak{g}^{'}}(X,Y)=2ntr(XY)$
$\mathfrak{g}$をLie代数とする。この時列
\begin{equation}
\mathfrak{g}=D^{0}\mathfrak{g}\supset D^{1}\mathfrak{g}\supset\cdots D^{k}\mathfrak{g}\coloneqq [D^{k-1}\mathfrak{g},D^{k-1}\mathfrak{g}]\supset
\end{equation}
を$\mathfrak{g}$の導来列と呼ぶ。またある自然数$n\in\mathbb{N}$が存在して$D^{n}\mathfrak{g}=0$が成り立つとき可解Lie代数と呼ぶ。
可換なLie代数$\mathfrak{g}$は可解Lie代数
\begin{eqnarray}
\forall X,Y\in\mathfrak{g}:[X,Y]=XY-YX=0
\end{eqnarray}
なので$D^{1}\mathfrak{g}=[\mathfrak{g},\mathfrak{g}]=0$。ゆえに$\mathfrak{g}$は可解Lie代数。
上三角行列の全体$\mathfrak{Tri}(n,\mathbb{R})\coloneqq\{\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\0&a_{22}&\cdots&a_{2n}\\\cdots&\cdots&\cdots&\cdots\\0&0&\cdots&a_{nn}\end{pmatrix}\in M(n,\mathbb{R})|a_{11},a_{12,...,a_{nn}\in\mathbb{R}}\}$を定めると、これは可解なLie代数。
$X=\left(\begin{array}{@{}c|c@{}}x&\vb*{a}^{t}\\\hline O_{n-1,1}&\tilde{X}\end{array}\right),Y=\left(\begin{array}{@{}c|c@{}}y&\vb*{b}^{t}\\\hline O_{n-1,1}&\tilde{Y}\end{array}\right)$とすると
\begin{eqnarray}
[X,Y]&=&XY-YX\\
&=&\left(\begin{array}{@{}c|c@{}}xy&x\vb*{b}^{t}+\vb*{a}^{t}\tilde{Y}\\\hline O_{n-1,1}&\tilde{X}\tilde{Y}\end{array}\right)-\left(\begin{array}{@{}c|c@{}}yx&y\vb*{a}^{t}+\vb*{b}^{t}\tilde{X}\\\hline O_{n-1,1}&\tilde{Y}\tilde{X}\end{array}\right)\\
&=&\left(\begin{array}{@{}c|c@{}}0&x\vb*{b}^{t}-y\vb*{a}^{t}+\vb*{a}^{t}\tilde{Y}-\vb*{b}^{t}\tilde{X}\\\hline O_{n-1,1}&[\tilde{X},\tilde{Y}]\end{array}\right)\\
&=&\left(\begin{array}{@{}c|c@{}}O_{n-1,1}&A\\\hline 0&0\end{array}\right)\quad(A\in \mathfrak{Tri}(n-1,\mathbb{R}))
\end{eqnarray}
以上の計算から、帰納的に計算する事で$D^{n}\mathfrak{Tri}(n,\mathbb{R})=0$を得るので可解。
$\mathfrak{g}$をLie代数とする。すると下記の事が成り立つ。
- $\mathfrak{g}$が可解であるとする。この時、$\mathfrak{g}$の任意の部分Lie代数$\mathfrak{h}$と$\mathfrak{g}$上の準同型射$\phi$に対して$\mathfrak{h},\phi(\mathfrak{g})$は共に可解
- $\mathfrak{I}$を$\mathfrak{g}$の可解イデアルとし、$\mathfrak{g}/\mathfrak{I}$も可解であるとすると、$\mathfrak{g}$も可解となる。
- $\mathfrak{I},\mathfrak{J}$ともに$\mathfrak{g}$の可解なイデアルであるとするとそのイデアルの和$\mathfrak{I}+\mathfrak{J}$も可解イデアルとなる。
[1]$\mathfrak{h}\subset\mathfrak{g}$なので$D^{k}\mathfrak{h}\subset D^{k}\mathfrak{g}$であるから$\mathfrak{g}$が可解なら$\mathfrak{h}$も可解
以下$\phi(\mathfrak{g})=\mathfrak{k}$とする。この時$\mathfrak{k}$が可解である事を証明する。
\begin{eqnarray}
\phi(D^{0}\mathfrak{g})&=&\phi(\mathfrak{g})\\
&=&\mathfrak{k}\\
&=&D^{0}\mathfrak{k}
\end{eqnarray}
よって$k=0$の場合は成り立つ。
そこで$1,2,....,k$まで$\phi(D^{k}\mathfrak{g})=D^{k}\mathfrak{k}$が成り立つと仮定する。
すると
\begin{eqnarray}
\phi(D^{k+1}\mathfrak{g})&=&\phi[D^{k}\mathfrak{g},D^{k}\mathfrak{g}]\\
&=&[\varphi(D^{k}\mathfrak{g}),\varphi(D^{k}\mathfrak{g})]\\
&=&[D^{k}\mathfrak{k},D^{k}\mathfrak{k}]\\
&=&D^{k+1}\mathfrak{k}
\end{eqnarray}
が得られる。ゆえに、$\mathfrak{g}$が可解ならば$\mathfrak{k}$は可解。
[2]
可解性により
ある自然数$m,n$が存在して$D^{m}\mathfrak{I}=0,D^{n}(\mathfrak{g}/\mathfrak{I})=[\mathfrak{J}]$が成り立つ。
よって$D^{n}\mathfrak{g}\subset \mathfrak{I}$となる事が分かる。ゆえに$D^{m+n}\mathfrak{g}=0$が証明されたので$\mathfrak{g}$は可解
[3]準同型射$\phi:\mathfrak{I}\ni I\mapsto I+\mathfrak{J}\in (\mathfrak{I}+\mathfrak{J})/\mathfrak{J}$を考えれば、$(\mathfrak{I}+\mathfrak{J})/\mathfrak{J}$は[1]より可解。
また、$\mathfrak{I},(\mathfrak{I}+\mathfrak{J})/\mathfrak{J}$は可解なので[2]より$\mathfrak{I}+\mathfrak{J}$も可解。
$\mathfrak{S}\subset\mathfrak{g}$をイデアルとする。
この時、$\mathfrak{g}$の任意のイデアル$\mathfrak{I}$に対して$\mathfrak{I}\subset\mathfrak{S}$が成り立つならば$\mathfrak{S}$を極大イデアルと呼ぶ。また、$\mathfrak{S}=Rad{\mathfrak{g}}$の様に書き、根基と言う。
Lie代数$\mathfrak{g}$に対して以下の様な列を考える。
\begin{equation}
\mathfrak{g}=C^{0}\mathfrak{g}\supset C^{1}\mathfrak{g}=[\mathfrak{g},C^{0}\mathfrak{g}]\supset\cdots\supset C^{k}\mathfrak{g}=[\mathfrak{g},C^{k-1}\mathfrak{g}]\supset\cdots
\end{equation}
この時、ある自然数$n\in\mathbb{N}$が存在して$C^{n}\mathfrak{g}=0$を満たす場合冪零Lie代数と呼ぶ。
$\mathfrak{n}(n,\mathbb{R})=\{\begin{pmatrix}0&a_{12}&a_{13}&\cdots&a_{1n}\\0&0&a_{23}&\cdots&a_{2n}\\\cdots&\cdots&\cdots&\cdots&\cdots\\0&0&0&\cdots&0\end{pmatrix}|a_{12},...,a_{n-1n}\in\mathbb{R}\}$は冪零Lie代数
$X=\left(\begin{array}{@{}c|c@{}}0&\vb*{a}^{t}\\\hline O_{n-1,1}&\tilde{X}\end{array}\right),Y=\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\\\hline O_{n-1,1}&\tilde{Y}\end{array}\right)$とおく。
\begin{eqnarray}
[X,Y]&=&XY-YX\\
&=&\left(\begin{array}{@{}c|c@{}}0&\vb*{a}^{t}\tilde{Y}\\\hline O_{n-1,1}&\tilde{X}\tilde{Y}\end{array}\right)-\left(\begin{array}{@{}c|c@{}}0&\vb*{b}^{t}\tilde{X}\\\hline O_{n-1,1}&\tilde{Y}\tilde{X}\end{array}\right)\\
&=&\left(\begin{array}{@{}c|c@{}}0&\vb*{a}^{t}\tilde{Y}-\vb*{b}^{t}\tilde{X}\\\hline O_{n-1,1}&[\tilde{X},\tilde{Y}]\end{array}\right)\\
&=&\left(\begin{array}{@{}c|c@{}}O_{n-1,1}&Z\\\hline 0&0\end{array}\right)
\end{eqnarray}
ただし$Z\in\mathfrak{n}(n-1,\mathbb{R})$
後は帰納的に計算していけばよい。
$\mathfrak{g}$をLie代数とする。
- $\mathfrak{g}$が冪零であるとする。この時、任意の$\mathfrak{g}$の部分Lie代数$\mathfrak{h}$と$\mathfrak{g}$上の準同型射$\phi$に対して$\mathfrak{h},\phi(\mathfrak{g})$は冪零。
- $\mathfrak{g}/Z(\mathfrak{g})$が冪零である時、$\mathfrak{g}$は冪零
- $\mathfrak{g}$が冪零かつ$\mathfrak{g}\neq 0$であるとすると$Z(\mathfrak{g})\neq 0$
[1]$\mathfrak{h}\subset\mathfrak{g}$なので、$C^{k}\mathfrak{h}\subset C^{k}\mathfrak{g}$ゆえに$\mathfrak{g}$が冪零ならば$\mathfrak{h}$は冪零。
また、以下$\phi(\mathfrak{g})=\mathfrak{k}$の様に置くと
\begin{eqnarray}
\phi(C^{0}\mathfrak{g})&=&\phi(\mathfrak{g})\\
&=&\mathfrak{k}\\
&=&C^{0}\mathfrak{k}
\end{eqnarray}
ゆえに$0,1,2,...,k$まで$\phi(C^{k}\mathfrak{g})=C^{k}\mathfrak{k}$が成り立つと仮定する。すると
\begin{eqnarray}
\phi(C^{k+1}\mathfrak{g})&=&[\phi(\mathfrak{g}),\phi(C^{k}\mathfrak{g})]\\
&=&[\mathfrak{k},C^{k}\mathfrak{k}]\\
&=&C^{k+1}\mathfrak{k}
\end{eqnarray}
ゆえに、$\phi(\mathfrak{g})$が冪零である事が示された。
[2]$\mathfrak{g}/Z(\mathfrak{g})$が冪零であるならば、ある自然数$n\in\mathbb{N}$が存在して$C^{n}\mathfrak{g}\subset Z(\mathfrak{g})$が成り立つ。
ゆえに
\begin{eqnarray}
C^{n+1}\mathfrak{g}&=&[\mathfrak{g},C^{n}\mathfrak{g}]\\
&\subset&[\mathfrak{g},Z(\mathfrak{g})]\\
&=&0
\end{eqnarray}
[3]仮定より$\mathfrak{g}$は冪零なのである自然数$n\in\mathbb{N}$が存在して$C^{n}\mathfrak{g}=0$が成り立つ。
よって、$Z(\mathfrak{g})=C^{n-1}\mathfrak{g}\neq 0$とすれば良い。
$\mathfrak{g}$を冪零なLie代数であるとする。
すると冪零性から任意の$Y\in\mathfrak{g}$に対して適当な列$X_{1},X_{2},...,X_{n}\in\mathfrak{g}$が存在して$ad_{X_{1}}\circ\cdots \circ ad_{X_{n}}(Y)=0$が成り立つ。特に$X_{1}=X_{2}=\cdots=X_{n}=X$である場合$X$をad冪零元と言う。
$\mathfrak{g}$が冪零なLie代数であれば、任意の元$X\in\mathfrak{h}$はad冪零元
$\mathfrak{g}$は冪零ならば、ある自然数$n\in\mathbb{N}$に対して$C^{n}\mathfrak{g}=0$が成り立つ事から
\begin{eqnarray}
\forall X,Y\in\mathfrak{g}:[X,[X,[...,[X,Y\underbrace{]]]\cdots ]}_{n個}&=&(ad_{X})^{n}(Y)\\
&=&0
\end{eqnarray}
Lie代数$\mathfrak{g}$、$\mathfrak{h}$をイデアルとする。
この時、部分集合$\mathfrak{h}^{\perp}\coloneqq\{X\in\mathfrak{g}|B(X,\mathfrak{h})=0\}$はイデアル。
[1]
\begin{eqnarray}
\forall a,b\in\mathbb{R}:\forall X,Y\in \mathfrak{h}^{\perp}:B(aX+bY,\mathfrak{h})&=&aB(X,\mathfrak{h})+bB(Y,\mathfrak{h})\\
&=&0
\end{eqnarray}
より$aX+bY\in\mathfrak{h}^{\perp}$
[2]$\forall X,Y,Z\in \mathfrak{g}:B([X,Y],Z)+B(Y,[X,Z])=0$を用いるだけ
\begin{eqnarray}
\forall Y\in\mathfrak{g}:\forall X\in\mathfrak{h}^{\perp}:H\in\mathfrak{h}:B([Y,X],H)&=&B(X,[Y,H])👈[Y,H]\in\mathfrak{h}\\
&=&0
\end{eqnarray}
$\mathfrak{g}$をLie代数、$\mathfrak{I},\mathfrak{J}$をイデアルとする。この時$\mathfrak{I}\cap\mathfrak{J}$もイデアル
\begin{eqnarray} \forall Y\in\mathfrak{g}:X\in\mathfrak{I}\cap\mathfrak{J}&:&X\in\mathfrak{I}\land X\in\mathfrak{J}\\ &\Rightarrow&[Y,X]\in\mathfrak{I}\land [Y,X]\in\mathfrak{J}\\ &\Leftrightarrow&[Y,X]\in\mathfrak{I}\cap\mathfrak{J} \end{eqnarray}
$\mathfrak{g}$をLie代数、$\mathfrak{h}$をイデアル。そして$\mathfrak{h}^{\perp}\coloneqq\{X\in\mathfrak{g}|B(X,\mathfrak{h})=0\}$とする。
この時、Killing形式$B$が非退化であるとすると$\mathfrak{h}\cap\mathfrak{h}^{\perp}$は可換なイデアル。
\begin{eqnarray}
\forall X,Y\in\mathfrak{h}\cap\mathfrak{h}^{\perp}:\forall Z\in\mathfrak{g}:B([X,Y],Z)+B(Y,[X,Z])=0
\end{eqnarray}
であり、$[X,Z],Y\in \mathfrak{h}\cap\mathfrak{h}^{\perp}$なので$B([X,Y],Z)=0$
仮定より$B$は非退化なので$[X,Y]=0$が示されるので$\mathfrak{h}\cap\mathfrak{h}^{\perp}$は可換なイデアルとなる事が証明された。
$V$を実ベクトル空間、$<,>$を$V$状の双一次形式とする。部分空間$W\subset V$に対して、$V$の部分空間$W^{\perp}\coloneqq \{v\in V|< v,W>=0\}$と定める。この時、下記の式が成り立つ。
\begin{equation}
\dim{W}+\dim{W^{\perp}}=\dim{V}+\dim{(W\cap W^{\perp})}
\end{equation}
[1]以下、$U\coloneqq (V\setminus W)\cup\{0\}$の様なベクトル空間を考える。
また次の様に基底を取る。
\begin{eqnarray}
\left\{
\begin{array}{l}
W=span\{e_{1},e_{2},...,e_{m}\}\\
U=span\{f_{1},f_{2},...,f_{n}\}
\end{array}
\right.
\end{eqnarray}
すると$W\oplus U=V=span\{e_{1},e_{2},...,e_{m},f_{1},f_{2},...,f_{n}\}$と書けるので$\dim{W}+\dim{U}=m+n=\dim{V}$
[2]今度は次の様に記号を定める。
\begin{eqnarray}
\left\{
\begin{array}{l}
< e_{i},e_{j}>=P_{ij}\\
< f_{i},e_{j}>=Q_{ij}
\end{array}
\right.
\end{eqnarray}
任意のベクトル$v\in V$は適当な実数$c_{1},c_{2},...,c_{m},d_{1},d_{2},...,d_{n}\in\mathbb{R}$を用いて次の様に書ける:$v=\sum_{k=1}^{m}c_{k}e_{k}+\sum_{l=1}^{n}d_{l}f_{l}$
これを用いると
\begin{eqnarray}
< v,\sum_{i=1}^{m}a_{i}e_{i}>&=&\sum_{k=1}^{m}\sum_{i=1}^{m}c_{k}P_{ki}a_{i}+\sum_{l=1}^{n}\sum_{i=1}^{n}d_{l}Q_{li}a_{i}\\
&=&0
\end{eqnarray}
[3]$\sum_{i=1}^{m}a_{i}e_{i}$は任意なので結局次の式と等価である事が分かる。
\begin{eqnarray}
\left\{
\begin{array}{l}
\sum_{k=1}^{m}c_{k}P_{k1}+\sum_{l=1}^{n}d_{l}Q_{l1}=0\\
\sum_{k=1}^{m}c_{k}P_{k2}+\sum_{l=1}^{n}d_{l}Q_{l2}=0\\
\cdots\\
\sum_{k=1}^{m}c_{k}P_{km}+\sum_{l=1}^{n}d_{l}Q_{lm}=0
\end{array}
\right.
\end{eqnarray}
ここで以下の様に記号を定めれば
\begin{eqnarray}
\left\{
\begin{array}{l}
P\coloneqq\begin{pmatrix}P_{11}&P_{12}&\cdots&P_{1m}\\P_{21}&P_{22}&\cdots&P_{2m}\\\cdots&\cdots&\cdots&\cdots\\P_{m1}&P_{m2}&\cdots&P_{mm}\end{pmatrix}\\
Q\coloneqq\begin{pmatrix}Q_{11}&Q_{12}&\cdots&Q_{1m}\\Q_{21}&Q_{22}&\cdots&Q_{2m}\\\cdots&\cdots&\cdots&\cdots\\Q_{n1}&Q_{n2}&\cdots&Q_{nm}\end{pmatrix}
\end{array}
\right.
\end{eqnarray}
以下の様な連立方程式を得る事が出来る。
\begin{equation}
\left(\begin{array}{@{}c|c@{}}P^{t}&Q^{t}\end{array}\right)\begin{pmatrix}c_{1}\\c_{2}\\\vdots\\c_{m}\\d_{1}\\d_{2}\\\vdots\\d_{n}\end{pmatrix}=0
\end{equation}
[4]この式から$\dim{W^{\perp}}=Ker{W^{\perp}}=\dim{V}-\rank{\left(\begin{array}{@{}c|c@{}}P^{t}&Q^{t}\end{array}\right)}$が得られる。
[5][1]の結果を代入すると
\begin{eqnarray}
\dim{W}+\dim{W^{\perp}}=\dim{V}+m-\rank{\left(\begin{array}{@{}c|c@{}}P^{t}&Q^{t}\end{array}\right)}
\end{eqnarray}
よって証明すべきは次式となる。
\begin{equation}
\dim{(W\cap W^{\perp})}=m-\rank{\left(\begin{array}{@{}c|c@{}}P^{t}&Q^{t}\end{array}\right)}
\end{equation}
[6]また$\rank{\left(\begin{array}{@{}c|c@{}}P^{t}&Q^{t}\end{array}\right)}=\rank{P}$であり、$W\cap W^{\perp}$は$Q=0$の場合を考えればいいので、$\dim{(W\cap W^{\perp})}=m-\rank{P}$。
以上をまとめると
\begin{equation}
\dim{W}+\dim{W^{\perp}}=\dim{V}+\dim{(W\cap W^{\perp})}
\end{equation}
次元公式にて双一次形式が非退化である場合下記の式が成り立つ。
\begin{equation}
\dim{W}+\dim{W^{\perp}}=\dim{V}
\end{equation}
[1]まず非退化な双一次形式として$B:V\times V\rightarrow \mathbb{R}$を考える。
[2]そして$W^{\ast}\coloneqq Hom(W,\mathbb{R})$として次の様な写像を考える。
\begin{equation}
\varphi:V\ni v\mapsto B(v,\cdot)\in W^{\ast}
\end{equation}
[3]
\begin{eqnarray}
W^{\perp}&=&\{X\in V|B(X,W)=0\}\\
&=&Ker{\varphi}
\end{eqnarray}
[4]また次の様な写像を考える。
\begin{equation}
\beta:V\ni v\mapsto B(v,\cdot)\in V^{\ast}
\end{equation}
すると、非退化性より、$B(v,V)=0\Rightarrow v=0$が得られる。ゆえに$Ker(\beta)=\{0\}$が証明された。
つまり$V\simeq V^{\ast}$である事が証明される。
[5]そこで、包含写像$id|_{W}:W\rightarrow V$を考え、さらに双対写像$id|_{W}^{\ast}:V^{\ast}\ni \lambda\mapsto \lambda|_{W}\in W^{\ast}$を考えれば$V$から$W$への全射な写像が構成出来る。
これから$\varphi=id|_{W}^{\ast}\circ \beta$が得られるので$\varphi$は全射である事が分かる。
[6]また$\dim{V}=\dim{Ker{\varphi}}+\dim{Im{\varphi}}$であり、$Ker{\varphi}=W^{\perp},\dim{Im}{\varphi}=\dim{W}^{\ast}=\dim{W}$
[7]ゆえに以上をまとめると
\begin{equation}
\dim{V}=\dim{W^{\perp}}+\dim{W}
\end{equation}
単純なLie代数$\mathfrak{g}$のKilling形式$B$は非退化
実際$Ker{B}=\{X\in \mathfrak{g}|B(X,\mathfrak{g})=0\}$とすると、$ker{B}$はイデアルなので$Ker{B}=\{0\}$または$\mathfrak{g}$
[1]$\mathfrak{g}=Ker{B}$であるとすると、$\mathfrak{g}$は可解Lie代数になる。
しかし、$\mathfrak{g}$はイデアルなので$[\mathfrak{g},\mathfrak{g}]=\mathfrak{g}\neq 0$なので矛盾。
[2]ゆえに、$Ker{B}=0$なので$B$は非退化である事が証明された。
$\mathfrak{g}$が半単純Lie代数$\Leftrightarrow$killing形式$B$が非退化
[$\Leftarrow$]$\mathfrak{h}\subset\mathfrak{g}$をイデアルとする。また$\mathfrak{h}^{\perp}\coloneqq\{X\in\mathfrak{g}|B(X,\mathfrak{h})=0\}$の様に定める。すると$B$は非退化なので
\begin{equation}
\dim{\mathfrak{g}}=\dim{\mathfrak{h}}+\dim{\mathfrak{h}^{\perp}}
\end{equation}
の様に書ける。この事から、以下の直和分解を得る。
\begin{equation}
\mathfrak{g}=\mathfrak{h}\oplus\mathfrak{h}^{\perp}
\end{equation}
また、$B$の$\mathfrak{h},\mathfrak{h}^{\perp}$への制限はそれぞれ、$\mathfrak{h},\mathfrak{h}^{\perp}$の非退化なkilling形式になる。
ゆえに帰納的に同じ議論を繰り返す事で$\mathfrak{h},\mathfrak{h}^{\perp}$が半単純である事が証明される。
[$\Rightarrow$]$\mathfrak{g}$は半単純であるとする。すると単純なLie代数$\mathfrak{g}^{k}\quad(k\in\mathbb{Z})$を用いて$\mathfrak{g}=\bigoplus_{k\in\mathbb{Z}}\mathfrak{g}^{k}$の様に直和分解できる。
また、下記の様に計算できる。
\begin{eqnarray}
\forall X\in \mathfrak{g}^{k},Y\in\mathfrak{g}^{l}:[X,Y]\in\mathfrak{g}^{k}\cap\mathfrak{g}^{l}=\{0\}\quad(k\neq l)
\end{eqnarray}
それゆえに
\begin{eqnarray}
\forall X\in\mathfrak{g}^{k},\forall Y\in\mathfrak{g}^{l}:\forall Z\in\mathfrak{g}:ad_{X}\circ ad_{Y}(Z)&=&[X,[Y,\sum_{k\in\mathbb{Z}}c_{k}Z_{k}]]\\
&=&\sum_{k\in\mathbb{Z}}c_{k}[X,[Y,Z_{k}]]\\
&=&c_{l}[X,[Y,Z_{l}]]\\
&=&-c_{l}([Y,[Z_{l},X]]+[Z_{l},[X,Y]])\\
&=&-c_{l}[Y,[Z_{l},X]]\\
&=&0
\end{eqnarray}
ゆえに$\forall X\in\mathfrak{g}^{k},\forall Y\in\mathfrak{g}^{l}:ad_{X}\circ ad_{Y}=0$が示される。
この事から
\begin{eqnarray}
\left\{
\begin{array}{l}
\forall X\in\mathfrak{g}:\exists X_{k}\in\mathfrak{g}^{k}\ s.t.\ X=\sum_{k\in\mathbb{Z}}X_{k}\\
\forall Y\in\mathfrak{g}:\exists Y_{k}\in\mathfrak{g}^{k}\ s.t.\ Y=\sum_{k\in\mathbb{Z}}Y_{k}\\
B(X,Y)=\sum_{k\in\mathbb{Z}}B(X_{k},Y_{k})
\end{array}
\right.
\end{eqnarray}
ここで$B(X_{k},Y_{k})=B|_{\mathfrak{g}^{k}\times\mathfrak{g}^{k}}(X_{k},Y_{k})$であり、$\mathfrak{g}^{k}$は単純なLie代数ので$B$は非退化。
半単純なLie代数$\mathfrak{g}$の部分Lie代数$\mathfrak{h}$が次の性質を満たす時、$\mathfrak{h}$をCartan部分代数と呼ぶ。
- $\forall X\in\mathfrak{h}:ad_{X}$は対角化可能
- 1.の条件を満たすもので$\mathfrak{h}$は極大
Cartan部分代数は可換
$\exists X,Y\in\mathfrak{h}\ s.t.\ 0\neq [X,Y]\in\mathfrak{h}$が成立したとする。
$ad_{X}$は対角化出来るので、$\mathfrak{h}$は固有値分解できる。
それを$\mathfrak{h}=\bigoplus_{\lambda}\mathfrak{h}_{\lambda}$の様に書く。
仮定より$0$でない固有値$\lambda$に対する固有ベクトルを$E_{\lambda}$とすれば
\begin{equation}
ad_{X}(E_{\lambda})=[X,E_{\lambda}]=\lambda E_{\lambda}
\end{equation}
が成り立つ。
また、$E_{\lambda}\in\mathfrak{h}$なので、$E_{\lambda}$も対角化可能
そこで$\mathfrak{h}=\bigoplus_{\mu}\overline{\mathfrak{h}}_{\lambda\mu}$の様に新たに固有値分解する。
すると以下の様に計算できるので$E_{\lambda}\in\mathfrak{h}_{\lambda 0}$
\begin{equation}
ad_{E_{\lambda}}(E_{\lambda})=[E_{\lambda},E_{\lambda}]=0
\end{equation}
また$X=\sum_{\mu}X_{\mu}F_{\mu}$の様に固有値ベクトルを用いて展開する。
すると
\begin{eqnarray}
ad_{E_{\lambda}}(X)&=&\sum_{\mu}X_{\mu}[E_{\lambda},F_{\mu}]\\
&=&\sum_{\mu}\mu X_{\mu}F_{\mu}\\
&=&-\lambda E_{\lambda}\in\mathfrak{h}_{\lambda0}
\end{eqnarray}
が得られる。
$\mathfrak{h}$は直和で書けるので、$\mu\neq 0$の場合は$X_{\mu}=0$であり、結局$\lambda E_{\lambda}=0$が導かれ$E_{\lambda}\neq 0$なので$\lambda=0$矛盾
ゆえに、$[X,Y]=0$でなければならない。
👆上記の証明から直ちに、$ad_{X}|_{\mathfrak{h}}$の固有値は$0$である事が分かる。
ルート
$\mathfrak{g}$を半単純なLie代数、$\mathfrak{h}$をカルタン部分代数とする。
この時、下記の性質を満たす双対写像$\alpha\in\mathfrak{h}^{\ast}$をルートと呼ぶ。
\begin{equation}
\exists X\in\mathfrak{g},\exists \alpha\in\mathfrak{h}^{\ast}\ s.t.\ ad_{H}(X)=\alpha(H)X
\end{equation}
$\mathfrak{g}$を半単純なLie代数、$\mathfrak{h}$をカルタン部分代数とする。また次の様な記号を導入する。
\begin{eqnarray}
\left\{
\begin{array}{l}
\mathfrak{g}_{\alpha}\coloneqq\{X\in\mathfrak{g}|ad(H)X=\alpha(H)X,\forall H\in\mathfrak{h}\}\\
\Delta=\{\alpha\in\mathfrak{h}^{\ast}|\alpha(H)\not\equiv 0,\forall H\in\mathfrak{h}\}
\end{array}
\right.
\end{eqnarray}
そして次の様に直和分解を行う。
\begin{eqnarray}
\mathfrak{g}=\mathfrak{h}\oplus\sum_{\alpha\in\Delta}\mathfrak{g}_{\alpha}
\end{eqnarray}
この直和分解をルート分解、$\Delta$の事をルート系と言う。
- $0$でないルート$\alpha$に対して$\dim{\mathfrak{g}_{\alpha}}=1$
- $[\mathfrak{g}_{\alpha},\mathfrak{g}_{\beta}]\subset\mathfrak{g}_{\alpha+\beta}$特に、$\alpha+\beta$がルートでない場合は$\forall X\in\mathfrak{g}_{\alpha},\forall Y\in\mathfrak{g}_{\beta}:[X,Y]=0$
1.$0$でないルート$\alpha$に対して$\dim{\mathfrak{g}_{\alpha}}=1$を証明する。
[1]まず$0$でないルート$\alpha\in\Delta$が存在した場合$-\alpha\in\Delta$も存在する事も示す。
実際$\exists \alpha\in\mathfrak{h}^{\ast},\exists X\in \mathfrak{g}\ s.t.\ \forall H\in\mathfrak{h}:ad_{H}X=\alpha(H)X$が成り立つ。
また、この$X$を用いると
\begin{eqnarray}
ad_{-H}(X)&=&[-H,X]\\
&=&-[H,X]\\
&=&-ad_{H}(X)\\
&=&-\alpha(H)X
\end{eqnarray}
ゆえに、$-\alpha\in\Delta$も示された。
[2]次にルート分解$\mathfrak{g}=\mathfrak{h}\bigoplus_{\alpha\in\Delta}\mathfrak{g}_{\alpha}$の内$\overline{\mathfrak{g}}_{\alpha}\coloneqq\mathfrak{g}_{-\alpha}\oplus\mathfrak{g}_{\alpha}\oplus span\{[E,F]\coloneqq G\}\quad(E\in \mathfrak{g}_{-\alpha},F\in\mathfrak{g}_{\alpha})$の様に定めると$\overline{\mathfrak{g}}_{\alpha}\simeq \mathfrak{sl}_{2}$である事を証明する。
実際
\begin{eqnarray}
\forall X\in\mathfrak{g}_{-\alpha},Y\in\mathfrak{g}_{\alpha}:ad_{H}([X,Y])次に&=&[H,[X,Y]]\\
&=&-[X,[Y,H]]-[Y,[H,X]]\\
&=&[X,[H,Y]]+[[H,X],Y]\\
&=&[X,ad_{H}(Y)]+[ad_{H}X,Y]\\
&=&-\alpha(H)[X,Y]+\alpha(H)[X,Y]\\
&=&0
\end{eqnarray}
なので$[E,F]=G\in\mathfrak{h}$が分かる。
以上の計算により下記の式が得られる。
\begin{eqnarray}
\left\{
\begin{array}{l}
[G,E]=-\alpha(G)E\\
[G,F]=\alpha(G)F\\
[E,F]=G\in\mathfrak{h}
\end{array}
\right.
\end{eqnarray}
[3]次に$\varphi:\mathfrak{h}\ni H\mapsto B(H,)\in\mathfrak{h}^{\ast}$を定めると、$\varphi$が同型写像を定めている事を示す。
実際、$\varphi$は準同型性を持つ事は次の計算により確かめられる。
\begin{eqnarray}
B(\alpha H+\beta \overline{H},\ast)&=&\alpha B(H,\ast)+\beta B(\overline{H},\ast)\\
&=&\alpha\varphi(H)+\beta\varphi(\overline{H})👈Bは双一次形式なので第二引数を固定すれば線形写像として振る舞う事を利用
\end{eqnarray}
これより$Ker{\varphi}=0$を示せばよい。
実際、$Ker{\varphi}=\{H\in\mathfrak{h}|\forall \overline{H}\in\mathfrak{h}:B(H,\overline{H})=B|_{\mathfrak{h}\times\mathfrak{h}}(H,\overline{H})=0\}$なので$B|_{\mathfrak{h}\times\mathfrak{h}}$は非退化である事を示せば、$Ker{\varphi}=0$が得られる。
ゆえに$\varphi$は単射。
以上の議論より$\mathfrak{h}\simeq \mathfrak{h}^{\ast}$が示せる。
そこで$B|_{\mathfrak{h}\times \mathfrak{h}}$が非退化である事を示す。
(1)交差項について
\begin{eqnarray}
\forall H\in\mathfrak{h},\forall X\in\mathfrak{g}_{\alpha},Y\in\mathfrak{g}_{\beta}:ad_{H}\circ ad_{X}(Y)&=&[H,[X,Y]]\\
&=&-[X,[Y,H]]-[Y,[H,X]]\\
&=&[X,[H,Y]]+[[H,X],Y]\\
&=&(\alpha+\beta)(H)[X,Y]
\end{eqnarray}
次に正規直交基底系$\{E_{\alpha},i\}\in\mathfrak{g}_{\alpha}$を考える。すると以下の様に書ける。
\begin{eqnarray}
B(H,X)&=&\sum_{\beta\in\Delta}\sum_{i}< E_{\beta,i}|ad_{H}\circ ad_{X}(E_{\beta,i})>\\
&=&\sum_{\beta\in\Delta}\sum_{i}(\alpha+\beta)(H)< E_{\beta,i}|[X,E_{\beta,i}]>\\
&=&\sum_{\beta\in\Delta}\sum_{i,j}(\alpha+\beta)(H)c_{\alpha+\beta,ij}< E_{\beta,i}|E_{\alpha+\beta,j}>\\
&=&\sum_{\beta\in\Delta}\sum_{i,j}(\alpha+\beta)(H)c_{\alpha+\beta,ij}\delta_{\beta,\alpha+\beta}\delta_{i,j}👈\alpha\neq 0\\
&=&0
\end{eqnarray}
ゆえに$B|_{\mathfrak{h}\times \mathfrak{h}}$は非退化。
(2)これより、
\begin{eqnarray}
\exists H\in\mathfrak{h}\ s.t.\ \forall X\in\mathfrak{h}:B(H,X)=0
\end{eqnarray}
が成り立つとする。しかし、$\forall \alpha\in\Delta:B(H,\mathfrak{g}_{\alpha})=0$であり、$B$は非退化なので$H=0$が得られる。
[4]上記の計算により$\mathfrak{h}\simeq\mathfrak{h}^{\ast}$なのでルート$\alpha\in\mathfrak{h}^{\ast}$に対して適当な$H_{\alpha}\in\mathfrak{h}$が存在して$\alpha\coloneqq B(H_{\alpha},)$が得られる。👈$H_{\alpha}$はco-rootと呼ばれる。
[5]このコルート$H_{\alpha}$を用いると$G=H_{\alpha}$が得られるので
\begin{eqnarray}
\left\{
\begin{array}{l}
[H_{\alpha},E]=-\alpha(H_{\alpha})E\\
[H_{\alpha},F]=\alpha(H_{\alpha})F\\
[E,F]=H_{\alpha}\in\mathfrak{h}
\end{array}
\right.
\end{eqnarray}
[6]次に$\mathfrak{h}^{\ast}$に内積$(\cdot|\cdot):\mathfrak{h}^{\ast}\times\mathfrak{h}^{\ast}\rightarrow \mathbb{R}$を次の様に定義する。
\begin{equation}
\forall \alpha,\beta\in\mathfrak{h}^{\ast}:\exists H_{\alpha},H_{\beta}\in\mathfrak{h}\ s.t.\ (\alpha|\beta)\coloneqq B(H_{\alpha},H_{\beta})
\end{equation}
一応、これが内積の性質を持つ事も確認する。
(1)双線形性
\begin{eqnarray}
\forall p,q\in\mathbb{R}:\forall \alpha,\beta,\gamma\in\mathfrak{h}^{\ast}:\exists H_{\alpha},H_{\beta},H_{\gamma}\in\mathfrak{h}\ s.t.\ (p\alpha+q\beta|\gamma)&=&B(pH_{\alpha}+qH_{\beta},H_{\gamma})\\
&=&pB(H_{\alpha},H_{\gamma})+qB(H_{\beta},H_{\gamma})\\
&=&p(\alpha|\gamma)+q(\beta|\gamma)
\end{eqnarray}
\begin{eqnarray}
\forall p,q\in\mathbb{R}:\forall \alpha,\beta,\gamma\in\mathfrak{h}^{\ast}:\exists H_{\alpha},H_{\beta},H_{\gamma}\in\mathfrak{h}\ s.t.\ (\alpha|p\beta+q\gamma)&=&B(H_{\alpha},pH_{\beta}+qH_{\gamma})\\
&=&pB(H_{\alpha},H_{\beta})+qB(H_{\alpha},H_{\gamma})\\
&=&p(\alpha|\beta)+q(\alpha|\gamma)
\end{eqnarray}
(2)非退化性$(\alpha|\alpha)=B(H_{\alpha},H_{\alpha})=0$が成り立つとすると、$B$の非退化性により$H_{\alpha}=0$が得られるので$\alpha=0$
(3)正定値性
\begin{eqnarray}
(\alpha|\alpha)&=&B(H_{\alpha},H_{\alpha})\\
&=&\sum_{\beta\in\Delta}\sum_{i}< E_{\beta,i}|[H_{\alpha},[H_{\alpha},E_{\beta,i}]]>\\
&=&\sum_{i}\alpha^{2}(H_{\alpha})< E_{\alpha,i}|E_{\alpha,i}>\\
&=&\sum_{i}\alpha^{2}(H_{\alpha})\geq 0
\end{eqnarray}
[7]以上の計算により、以下の様に定める事で下記の式が得られる。
\begin{eqnarray}
\left\{
\begin{array}{l}
\overline{H}_{\alpha}\coloneqq -\frac{2}{(\alpha|\alpha)}[E,F]\\
\overline{E}\coloneqq \sqrt{\frac{2}{(\alpha|\alpha)}}E\\
\overline{F}\coloneqq \sqrt{\frac{2}{(\alpha|\alpha)}}F\\
[\overline{H}_{\alpha},\overline{E}]=-2\overline{E}\\
[\overline{H}_{\alpha},\overline{F}]=2\overline{F}\\
[\overline{E},\overline{F}]=-\overline{H}_{\alpha}
\end{array}
\right.
\end{eqnarray}
[8]$\mathfrak{sl}_{2}=span\{h=\begin{pmatrix}1&0\\0&-1\end{pmatrix},=e=\begin{pmatrix}0&0\\1&0\end{pmatrix},f=\begin{pmatrix}0&1\\0&0\end{pmatrix}\}$の様に定める。
すると、
\begin{eqnarray}
\left\{
\begin{array}{l}
[h,e]=-2e\\
[h,f]=2f\\
[e,f]=-h
\end{array}
\right.
\end{eqnarray}
上記の計算により、準同型射$\varphi:\overline{\mathfrak{g}_{\alpha}}\rightarrow \mathfrak{sl}_{2}$を次の様に構成する。
\begin{eqnarray}
\left\{
\begin{array}{l}
\varphi(\overline{E})=e\\
\varphi(\overline{F})=f\\
\varphi(\overline{H}_{\alpha})=h
\end{array}
\right.
\end{eqnarray}
するとこれは全単射になり同型射である事が簡単な計算により分かるので、$\dim{\overline{\mathfrak{g}}_{\alpha}}=3$。ゆえに$\dim{\mathfrak{g}_{\alpha}}=1$。
2.$[\mathfrak{g}_{\alpha},\mathfrak{g}_{\beta}]\subset\mathfrak{g}_{\alpha+\beta}$特に、$\alpha+\beta$がルートでない場合は$\forall X\in\mathfrak{g}_{\alpha},\forall Y\in\mathfrak{g}_{\beta}:[X,Y]=0$
$[X,Y]\in\mathfrak{g}_{\alpha+\beta}$なので以下の様に計算できる。
\begin{eqnarray}
ad_{H}([X,Y])&=&[H,[X,Y]]\\
&=&-[X,[Y,H]]-[Y,[H,X,]]\\
&=&[X,[H,Y]]+[[H,X],Y]\\
&=&\{\alpha(H)+\beta(H)\}[X,Y]
\end{eqnarray}
ここで$\alpha+\beta\not\in\Delta$なので$[X,Y]=0$しかありえない。
一応上記の計算で用いた内積について再定義しておく。
$\mathfrak{g}$を半単純、$\mathfrak{h}$をカルタン部分代数とする。
この時、killing形式$B$は$\mathfrak{h}$に制限したとき非退化である事が分かっているので、以下の様に書ける。
\begin{equation}
\forall \alpha\in\mathfrak{h}^{\ast}:\exists H_{\alpha}\in\mathfrak{h}\ s.t.\ \alpha=B(H_{\alpha},)
\end{equation}
この$H_{\alpha}$を$\alpha$に対するコルートと呼ぶ。
$\mathfrak{g}$を半単純、$\mathfrak{h}$をカルタン部分代数とする。
この時、内積$(,):\mathfrak{h}^{\ast}\times\mathfrak{h}^{\ast}\rightarrow \mathbb{R}$を次の様に定める。
\begin{equation}
\forall \alpha,\beta\in\mathfrak{h}^{\ast}:\exists H_{\alpha},H_{\beta}\in\mathfrak{h}\ s.t.\ (\alpha|\beta)\coloneqq B(H_{\alpha},H_{\beta})
\end{equation}
$\mathfrak{sl}_{2}$のルート系$\Delta$を構成せよ。
[1]下記の様に記号を定める。
\begin{eqnarray}
\left\{
\begin{array}{l}
h\coloneqq\begin{pmatrix}1&0\\0&-1\end{pmatrix}\\
e\coloneqq\begin{pmatrix}0&1\\0&0\end{pmatrix}\\
f\coloneqq\begin{pmatrix}0&0\\1&0\end{pmatrix}
\end{array}
\right.
\end{eqnarray}
[2]すると以下の様な交換関係が成り立つ事が分かる。
\begin{eqnarray}
\left\{
\begin{array}{l}
[h,e]=2e\\
[h,f]=-2f\\
[e,f]=h
\end{array}
\right.
\end{eqnarray}
[3]実は$\mathfrak{h}=\mathbb{R}h\subset\mathfrak{sl}_{2}$と定めるとこれはカルタン部分代数になる。これは
(1)可換性:これは$\dim{\mathfrak{h}}=1$より明らか。
(2)対角化可能:
\begin{eqnarray}
\left\{
\begin{array}{l}
ad_{h}(h)=[h,h]=0\\
ad_{h}(e)=[h,e]=2e\\
ad_{h}(e)=[h,f]=-2f\\
\end{array}
\right.
\end{eqnarray}
よって$ad_{h}$は$\mathfrak{sl}_{2}$上で対角化可能
(3)極大性
$\forall X\in\mathfrak{h}:\exists A,B,C\in\mathbb{R}\ s.t.\ X=Ah+Be+Cf$と書けるので
\begin{eqnarray}
[h,X]&=&A[h,h]+B[h,e]+C[h,f]\\
&=&B[h,e]+C[h,f]\\
&=&2Be-2Cf
\end{eqnarray}
$h,X$が可換であるとすると$[h,X]=0$であるが、$e,f$は一次独立であるため$B=C=0$が得られる。
(4)ゆえに$\mathbb{R}h$はカルタン部分代数。
先の計算より、$X=Be+Cf$とすると、次の式が成り立つので
\begin{equation}
ad_{h}(X)=2Be-2Cf
\end{equation}
これから次の様にしてルートを求める事が出来る。
$B=1,C=0$の場合$\alpha(h)=2$
また$B=0,C=1$の場合$\alpha(h)=-2$
ゆえに$\Delta=\{\pm\alpha\}$
$\mathfrak{sl}_{3}$のルート系$\Delta$を構成せよ。
また図次せよ。
[1]実は$\mathfrak{h}=\{H=\begin{pmatrix}a&0&0\\0&b&0\\0&0&-a-b\end{pmatrix}|a,b\in\mathbb{R}\}$とするとこれはCartan部分代数になる。
[2]
(1)可換性:これは対角行列は行列に関する積に関して可換なので明らか。
(2)対角化可能$h_{1}=a,h_{2}=b,h_{3}=-a-b$とおく
\begin{eqnarray}
ad_{H}(E_{ij})&=&[H,E_{ij}]\\
&=&h_{i}E_{ij}-h_{j}E_{ij}\\
&=&(h_{i}-h_{j})E_{ij}
\end{eqnarray}
なので、対角化可能性も示せた。
(3)極大性
$X=\displaystyle{\sum_{i\neq j}c_{ij}E_{ij}}$の様に置く。すると以下の式が得られる。
\begin{eqnarray}
ad_{H}(X)&=&[H,X]\\
&=&\sum_{i\neq j}c_{ij}[H,E_{ij}]\\
&=&\sum_{i\neq j}c_{ij}(h_{i}-h_{j})E_{ij}
\end{eqnarray}
この時、$[H,X]=0$が成り立つとすると、$E_{12},E_{13},...,E_{32}$は一次独立なので$c_{ij}=0\quad(i\neq j)$が得られる。
以上から$\mathfrak{h}$はCartan部分代数である事が示せた。
次にルート系についてだが(2)の計算により
\begin{equation}
\Delta=\{h_{i}-h_{j}|i\neq j\}
\end{equation}
が得られる。
また$h_{i}-h_{j}$のコルートを$H_{ij}=\frac{1}{6}(\delta_{ik}\delta_{il}-\delta_{jk}\delta_{jl})_{kl}$とすると
\begin{eqnarray}
B(H_{ij},H_{kl})&=&6tr(H_{ij}H_{kl})\\
&=&\sum_{m,n}(\delta_{im}\delta_{in}-\delta_{jm}\delta_{jn})(\delta_{kn}\delta_{km}-\delta_{ln}\delta_{lm})\\
&=&\sum_{m,n}(\delta_{im}\delta_{in}\delta_{kn}\delta_{km}-\delta_{im}\delta_{in}\delta_{ln}\delta_{lm}-\delta_{jm}\delta_{jn}\delta_{kn}\delta_{km}+\delta_{jm}\delta_{jn}\delta_{ln}\delta_{lm})\\
&=&\delta_{ik}-\delta_{il}-\delta_{jk}+\delta_{jl}
\end{eqnarray}
よって、
\begin{eqnarray}
(h_{i}-h_{j}|h_{i}-h_{j})&=&2
\end{eqnarray}
また、鳩ノ巣原理より$i,j,k,l$のどれかは必ず一致する。そこで$l=j$であるとすると
\begin{eqnarray}
(h_{i}-h_{j}|h_{k}-h_{j})&=&1
\end{eqnarray}
ゆえにルート$h_{i}-h_{j},h_{k}-h_{j}$のなす角を$\theta$とすると
\begin{eqnarray}
\cos{\theta}&=&\frac{(h_{i}-h_{j}|h_{k}-h_{j})}{\sqrt{(h_{i}-h_{j}|h_{i}-h_{j})}\sqrt{(h_{k}-h_{l}|h_{k}-h_{l})}}\\
&=&\frac{1}{2}
\end{eqnarray}
よって、$\theta=\pm\frac{\pi}{3}$
これを図示すると下記の様になる。
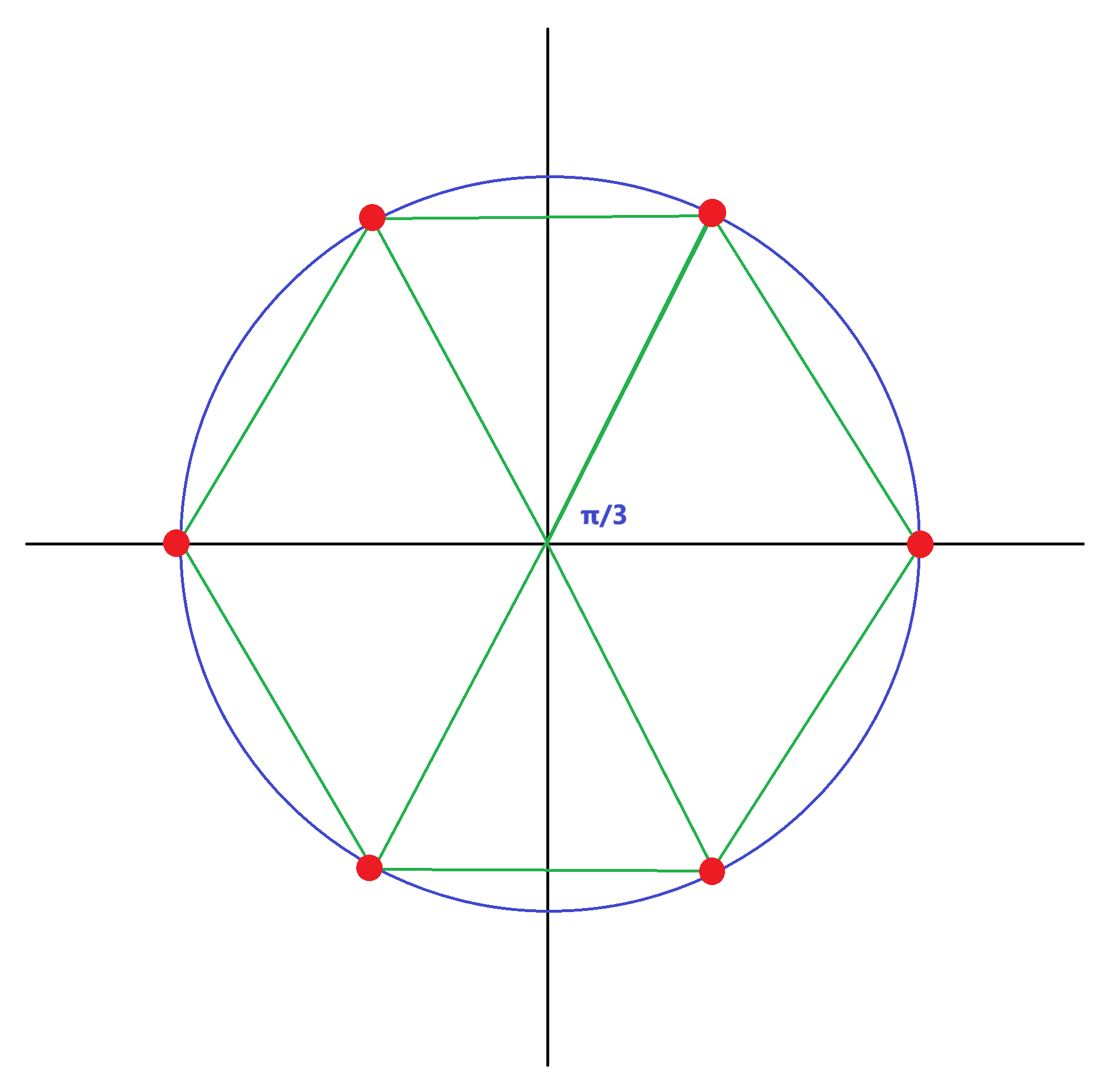
カルタン部分代数$\mathfrak{h}$の次元を$m$とする。この時ルート系$\Delta$の部分集合$\{\alpha_{k}\}_{k=1}^{m}$で以下の性質を満たすものを単純ルートと呼ぶ。
- $\{\alpha_{k}\}_{k=1}^{m}$は$\mathfrak{h}^{\ast}$の基底
- 任意のルート$\alpha\in\mathfrak{h}$は次の様な整数係数一次結合で書ける:$\exists c_{k}\in\mathbb{Z}_{\geq 0}\ s.t. \alpha=\sum_{k=1}^{m}c_{k}\alpha_{k}$または$\exists c_{k}\in\mathbb{Z}_{\geq 0}\ s.t. \alpha=-\sum_{k=1}^{m}c_{k}\alpha_{k}$時、単純ルートと呼ぶ。
なお、正整数のみを考えた単純ルートの一次結合全体を$\Delta_{+}$と書き正ルート。
負の場合を$\Delta_{-}$と書き、負ルートと呼ぶ。
あるルート$\omega\in\mathfrak{h}^{\ast}$について$\omega+\sum_{k=1}^{m}c_{k}\alpha_{k},c_{k}\geq 0$がルートになるのは$k=1,2,...,m$に対して$c_{k}=0$に限るとき$\omega$を極大ルートと呼ぶ。
$\mathfrak{sl}_{3}$の単純ルート、極大ルートを求めよ。
まず次の様に記号を定める。
\begin{eqnarray}
\left\{
\begin{array}{l}
\epsilon_{1}=h_{2}-h_{3}\\
\epsilon_{2}=h_{1}-h_{3}\\
\epsilon_{3}=h_{1}-h_{2}
\end{array}
\right.
\end{eqnarray}
$\mathfrak{sl}_{3}$のルート系は次の様に与えられている事を思い出そう。
\begin{equation}
\Delta=\{\pm\epsilon_{1},\pm\epsilon_{2},\pm\epsilon_{3}\}
\end{equation}
よって、単純ルートは次の様になる。$\{\epsilon_{1},-\epsilon_{2}\}$
また正ルートは
\begin{eqnarray}
\Delta_{+}=\{\epsilon_{1},-\epsilon_{2},\epsilon_{1}+(-\epsilon_{2})\}
\end{eqnarray}
また極大ルートは$\epsilon_{1}+(-\epsilon_{2})$
戸田格子への応用
質点$m_{1},m_{2},...,m_{n}$が位置$q_{1},q_{2},...,q_{n}$に置かれており、また質点$m_{i},m_{i+1(mod\ n)}\quad(i=1,2,...,n)$がばね定数$k$のばねにより繋がれているとする。
この様な質点系のハミルトニアン$H$を求めてくださ
また運動方程式を求めてください。
今回、質点により構成される輪は十分大きくかつ何も外力が加わっていない状態では円環と一致し、さらにばねは、常に接戦方向のみ伸縮し、質点の位置は円環のある点$O$を始点にし円環に沿って反時計回りに測った最短の弧長であるとする。
[1]
\begin{eqnarray}
H&=&\frac{1}{2}\sum_{k=1}^{n}\{m_{k}\dot{q_{k}}^{2}+k(q_{k+1(mod n)}-q_{k})^{2}\}\\
&=&\frac{1}{2}\sum_{k=1}^{n}\{\frac{p_{k}^{2}}{m_{k}}+k(q_{k+1(mod n)}-q_{k})^{2}\}
\end{eqnarray}
[2]
\begin{eqnarray}
\left\{
\begin{array}{l}
\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}=\frac{p_{i}}{m_{i}}\\
\dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}=k(q_{i+1(mod\ n)}-q_{i})-k(q_{i}-q_{i-1})=k(q_{i+1(mod\ n)}-2q_{i}+q_{i-1(mod\ n)})
\end{array}
\right.
\end{eqnarray}
上記の問題において、$m_{1}=m_{2}=\cdots=m_{n}=1$とし、ばねを非線形なばねに変更しその弾性エネルギーを$\frac{1}{2}e^{-(q_{i+1}-q_{i})}$の様にしたものを考える。
するとハミルトニアン$H$は次の様に書ける。
\begin{equation}
H=\frac{1}{2}\sum_{k=1}^{n}\{p_{k}^{2}+e^{-(q_{k+1(mod n)}-q_{k})}\}
\end{equation}
このハミルトニアンから得られる下記の微分方程式を戸田格子と言う。
\begin{eqnarray}
\left\{
\begin{array}{l}
\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}=p_{i}\\
\dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}=e^{q_{i-1}-q_{i}}-e^{q_{i}-q_{i+1}}
\end{array}
\right.
\end{eqnarray}
戸田格子にて下記の様に記号を定め直す。
\begin{eqnarray}
\left\{
\begin{array}{l}
a_{i}=\frac{1}{2}e^{\frac{q_{i}-q_{i+1}}{2}}\\
b_{i}=\frac{1}{2}p_{i}
\end{array}
\right.
\end{eqnarray}
すると、これらは下記の微分方程式を満たす。
\begin{eqnarray}
\left\{
\begin{array}{l}
\dot{a}_{i}=a_{i}(b_{i}-b_{i+1})\\
\dot{b}_{i}=2(a_{i-1}^{2}-a_{i}^{2})
\end{array}
\right.
\end{eqnarray}
次に以下の様な行列$L,A$を定義する。
\begin{eqnarray}
\left\{
\begin{array}{l}
L\coloneqq \begin{pmatrix}b_{1}&a_{1}&0&\cdots&0&1_{n}\\a_{1}&b_{2}&a_{2}&\cdots&0&0\\0&a_{2}&b_{3}&\cdots&0&0\\&&&\ddots&&\\0&0&0&\cdots&b_{n-1}&a_{n-1}\\a_{n}&0&0&\cdots&a_{n-1}&b_{n}\end{pmatrix}\\
A\coloneqq \begin{pmatrix}0&a_{1}&0&\cdots&0&-a_{1}\\-a_{1}&0&a_{2}&\cdots&0&0\\0&-a_{2}&0&\cdots&0&0\\&&&\ddots&0&0\\0&0&0&\cdots&0&a_{n-1}\\a_{n}&0&0&\cdots&-a_{n-1}&0\end{pmatrix}
\end{array}
\right.
\end{eqnarray}
すると以下の微分方程式を満たす事が分かる。
この微分方程式をLAX形式と言う。
\begin{equation}
\dot{L}=[L,A]
\end{equation}
上記LAX形式について$n=3$の場合で成り立つ事を確認せよ。
\begin{eqnarray}
\left\{
\begin{array}{l}
L=\begin{pmatrix}b_{1}&a_{1}&a_{3}\\a_{1}&b_{2}&a_{2}\\a_{3}&a_{2}&b_{3}\end{pmatrix}\\
A=\begin{pmatrix}0&a_{1}&-a_{3}\\-a_{1}&0&a_{2}\\a_{3}&-a_{2}&0\end{pmatrix}
\end{array}
\right.
\end{eqnarray}
\begin{eqnarray}
[L,A]&=&\begin{pmatrix}b_{1}&a_{1}&a_{3}\\a_{1}&b_{2}&a_{2}\\a_{3}&a_{2}&b_{3}\end{pmatrix}\begin{pmatrix}0&a_{1}&-a_{3}\\-a_{1}&0&a_{2}\\a_{3}&-a_{2}&0\end{pmatrix}-\begin{pmatrix}0&a_{1}&-a_{3}\\-a_{1}&0&a_{2}\\a_{3}&-a_{2}&0\end{pmatrix}\begin{pmatrix}b_{1}&a_{1}&a_{3}\\a_{1}&b_{2}&a_{2}\\a_{3}&a_{2}&b_{3}\end{pmatrix}\\
&=&\begin{pmatrix}-a_{1}^{2}+a_{3}^{2}&a_{1}b_{1}-a_{2}a_{3}&a_{1}a_{2}-a_{3}b_{1}\\-a_{1}b_{2}+a_{2}a_{3}&a_{1}^{2}-a_{2}^{2}&-a_{1}a_{3}+a_{2}b_{2}\\-a_{1}a_{2}+a_{3}b_{3}&a_{1}a_{3}-a_{2}b_{3}&a_{2}^{2}-a_{3}^{2}\end{pmatrix}-\begin{pmatrix}a_{1}^{2}-a_{3}^{2}&a_{1}b_{2}-a_{2}a_{3}&a_{1}a_{2}-a_{3}b_{3}\\-a_{1}b_{1}+a_{2}a_{3}&-a_{1}^{2}+a_{2}^{2}&-a_{1}a_{3}+a_{2}b_{3}\\-a_{1}a_{2}+a_{3}b_{1}&a_{1}a_{3}-a_{2}b_{2}&-a_{2}^{2}+a_{3}^{2}\end{pmatrix}\\
&=&\begin{pmatrix}2(a_{3}^{2}-a_{1}^{2})&a_{1}(b_{1}-b_{2})&a_{3}(b_{3}-b_{1})\\a_{1}(b_{1}-b_{2})&2(a_{1}^{2}-a_{2}^{2})&a_{2}(b_{2}-b_{3})\\a_{3}(b_{3}-b_{1})&a_{2}(b_{2}-b_{3})&2(a_{2}^{2}-a_{3}^{2})\end{pmatrix}\\
&=&\begin{pmatrix}\dot{b}_{1}&\dot{a}_{1}&\dot{a}_{3}\\\dot{a}_{1}&\dot{b}_{2}&\dot{a}_{2}\\\dot{a}_{3}&\dot{a}_{2}&\dot{b}_{3}\end{pmatrix}\\
&=&\dot{L}
\end{eqnarray}
\begin{eqnarray} \frac{d}{dt}L^{k}&=&kL^{k-1}\dot{L}\\ &=&kL^{k-1}[L,A] \end{eqnarray}
であり
\begin{eqnarray} tr(\frac{d}{dt}L^{k})&=&ktr(L^{k-1}[L,A])\\ &=&k\{tr(L^{k}A)-tr(L^{k-1}AL)\}\\ &=&k\{tr(L^{k}A)-tr(L^{k}A)\}\\ &=&0 \end{eqnarray}
ゆえに、$\frac{d}{dt}tr(L^{k})$が保存量になる事が分かる。
\begin{eqnarray}
\left\{
\begin{array}{l}
\vb*{\alpha}_{1}=(1,-1,0,0,...,0,0)^{t}\\
\vb*{\alpha}_{2}=(0,1,-1,0,...,0,0)^{t}\\
\vdots\\
\vb*{\alpha}_{n-1}=(0,0,0,0,...,1,-1)^{t}\\
\vb*{\alpha}_{n}=(-1,0,0,0,...,0,1)^{t}
\end{array}
\right.
\end{eqnarray}
を用いると$\vb*{q}\coloneqq\begin{pmatrix}q_{1}\\q_{2}\\\vdots\\q_{n}\end{pmatrix}$の様におけば戸田格子に関するハミルトニアンは下記の様に書ける事が分かる。
\begin{equation}
H=\frac{1}{2}\sum_{k=1}^{n}p_{k}^{2}+\sum_{k=1}^{n}e^{<\vb*{\alpha}_{k}|\vb*{q}>}
\end{equation}
これを一般化し、ベクトル列$\{\vb*{\alpha}_{k}\}$を任意に選んで出来るハミルトニアンから導かれる微分方程式を一般化戸田格子と呼ぶ。
以下一般化戸田格子がLAX形式で書ける条件について考察します。
$\mathfrak{g}$を半単純Lie代数とする。また、$\mathfrak{h}=span\{h_{1},h_{2},...,h_{n}\}$をカルタン部分代数とする。また、ルート系$\Delta$の部分集合$R\coloneqq \{\alpha_{1},\alpha_{2},...,\alpha_{m}|\alpha_{i}+\alpha_{j}は非零ルートにならない。\}\subset\Delta$を定める。
また、killing形式$B$に対して$B(e_{\alpha_{i}},e_{-\alpha_{i}})=1$となる様に$\mathfrak{g}_{\alpha_{i}}$の基底$e_{\alpha_{i}}$を取る。
上記条件のもと、ルート$\alpha_{i}$のコルートが$t_{\alpha_{i}}=\sum_{j=1}^{n}d_{ij}h_{j} $の様に書けたとする。
すると下記のハミルトニアンを持つ系はLAX形式で書ける。
\begin{equation}
H=\frac{1}{2}\sum_{k,l}B(h_{k},h_{l})p_{k}p_{l}+\sum_{k=1}^{m}e^{2\sum_{j=1}^{n}d_{kj}q_{j}}
\end{equation}
[1]$x_{k}\coloneqq e^{\sum_{j=1}^{n}d_{kj}q_{j}}$の様に置くと、
\begin{eqnarray}
\dot{x_{k}}&=&x_{k}\sum_{j=1}^{n}d_{kj}\dot{q}_{j}\\
&=&x_{k}\sum_{j=1}^{n}d_{kj}\frac{\partial H}{\partial p_{j}}\\
&=&x_{k}\frac{1}{2}\sum_{j,m,n}d_{kj}B(h_{m},h_{n})(\delta_{jm}p_{n}+p_{m}\delta_{jn})\\
&=&x_{k}\frac{1}{2}\sum_{j,n}d_{kj}B(h_{j},h_{n})p_{n}+\frac{1}{2}\sum_{j,m}d_{kj}B(h_{m},h_{j})p_{m}\\
&=&x_{k}\sum_{j,n}d_{kj}B(h_{j},h_{n})p_{n}\\
&=&x_{k}\sum_{i,j}d_{kj}p_{i}B(h_{j},h_{i})
\end{eqnarray}
\begin{eqnarray}
\dot{p}_{k}&=&-\frac{\partial H}{\partial q_{k}}\\
&=&-2\sum_{i=1}^{m}x_{i}\frac{\partial x_{i}}{\partial q_{k}}\\
&=&-2\sum_{i=1}^{m}x_{i}^{2}d_{ik}
\end{eqnarray}
[2]
次に、$\mathfrak{g}$の元を次の様に定める。
\begin{eqnarray}
\left\{
\begin{array}{l}
L\coloneqq\sum_{k=1}^{m}x_{k}(e_{\alpha_{k}}+e_{-\alpha_{k}})+\sum_{j=1}^{n}p_{j}h_{j}\\
A\coloneqq\sum_{k=1}^{m}x_{k}(e_{\alpha_{k}}-e_{-\alpha_{k}})
\end{array}
\right.
\end{eqnarray}
と定める。
するとこれは$\dot{L}=[L,A]$を満たす。
実際
\begin{eqnarray}
\left\{
\begin{array}{l}
[e_{\alpha_{i}},e_{\alpha_{j}}]=0👈\alpha_{i}+\alpha_{j}は非零ルートにならない\\
[e_{\alpha_{i}},e_{-\alpha_{i}}]=t_{\alpha_{i}}👈ルート系の性質で話た議論を踏襲\\
[h_{k},e_{\alpha_{i}}]=ad_{h_{k}}(e_{\alpha_{i}})=\alpha_{i}(h_{k})e_{\alpha_{i}}👈ルートの定義\\
[h_{j},h_{k}]=0👈カルタン部分代数は可換
\end{array}
\right.
\end{eqnarray}
を用いると下記の計算が出来る。
\begin{eqnarray}
[L,A]&=&\sum_{k,l}[x_{k}(e_{\alpha_{k}}+e_{-\alpha_{k}}),x_{l}(e_{\alpha_{l}}-e_{-\alpha_{l}})]+\sum_{k=1}^{m}\sum_{j=1}^{n}[p_{j}h_{j},x_{k}(e_{\alpha_{k}}-e_{-\alpha_{k}})]\\
&=&\sum_{k,l}x_{k}x_{l}([e_{\alpha_{k}},e_{\alpha_{l}}]-[e_{\alpha_{k}},e_{-\alpha_{l}}]+[e_{-\alpha_{k}},e_{\alpha_{l}}]-[e_{-\alpha_{k}},e_{-\alpha_{l}}])+\sum_{k=1}^{m}\sum_{j=1}^{n}p_{j}x_{k}([h_{j},e_{\alpha_{k}}]-[h_{j},e_{-\alpha_{k}}])\\
&=&-2\sum_{k}x_{k}^{2}t_{\alpha_{k}}+\sum_{k=1}^{m}\sum_{j=1}^{n}p_{j}x_{k}\alpha_{k}(h_{j})(e_{\alpha_{k}}+e_{-\alpha_{k}})\\
&=&-2\sum_{k}x_{k}^{2}t_{\alpha_{k}}+\sum_{k=1}^{m}\sum_{j=1}^{n}p_{j}x_{k}B(t_{\alpha_{k}},h_{j})(e_{\alpha_{k}}+e_{-\alpha_{k}})
\end{eqnarray}
\begin{eqnarray}
\dot{L}&=&\sum_{k=1}^{m}\dot{x}_{k}(e_{\alpha_{k}}+e_{-\alpha_{k}})+\sum_{j=1}^{n}\dot{p}_{j}h_{j}\\
&=&\sum_{k=1}x_{k}\sum_{i,j}d_{kj}p_{i}B(h_{j},h_{i})(e_{\alpha_{k}}+e_{-\alpha_{k}})-2\sum_{k=1}^{n}\sum_{i=1}^{m}x_{i}^{2}d_{ik}h_{k}\\
&=&-2\sum_{i}x_{i}^{2}t_{\alpha_{i}}+\sum_{k=1}^{m}\sum_{i=1}^{n}p_{i}x_{k}B(\sum_{j=1}^{n}d_{kj}h_{j},h_{i})(e_{\alpha_{k}}+e_{-\alpha_{k}})\\
&=&-2\sum_{i}x_{i}^{2}t_{\alpha_{i}}+\sum_{k=1}^{m}\sum_{i=1}^{n}p_{i}x_{k}B(t_{\alpha_{k}},h_{i})(e_{\alpha_{k}}+e_{-\alpha_{k}})
\end{eqnarray}
最後に、半単純Lie代数と同型な行列の集合で定義されたLie代数を用意すればそれは同型なのである適当な行列$L,A$を用いて$\dot{L}=[L,A]$と書ける。
ゆえに、LAX形式で書ける事が証明された。
