マルコフ圏,条件付き期待値(メモ)
$\C$をマルコフ圏とする.
条件付き期待値
$R\in\C$は次をみたすときregularであるという:
任意の$X\in\C$と任意の$\psi\colon I\to R\otimes X$に対し,conditional distribution $\psi_{|X}\colon X\to R$(F, Definition 11.1)が存在する.
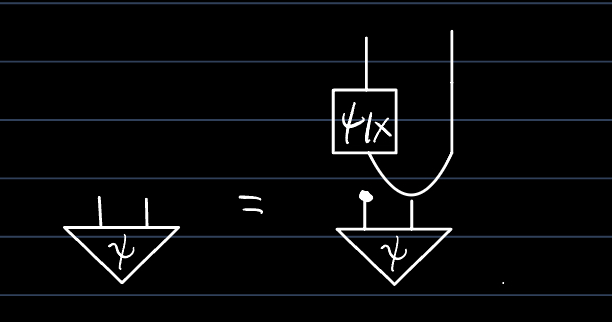
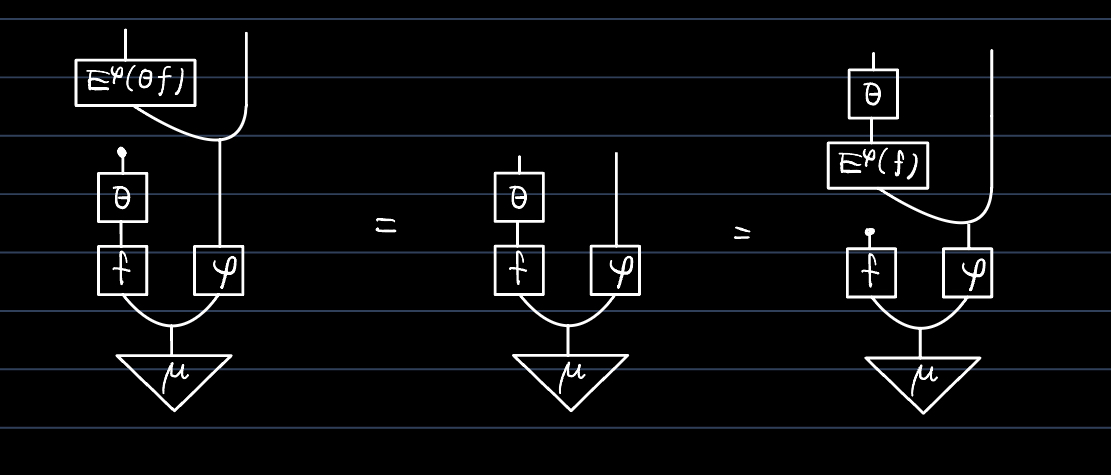
$R\in\C$をregular objectとし,$X\in\C$, $\mu\colon I\to X$とする.任意の$Y\in\C$と$\varphi\colon X\to Y$および$f\colon X\to R$に対し,$E^\varphi(f)\colon Y\to R$を以下のように定める:
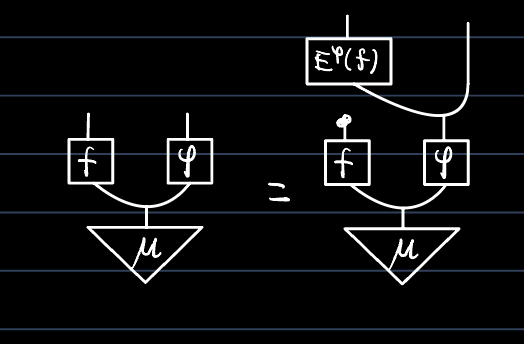
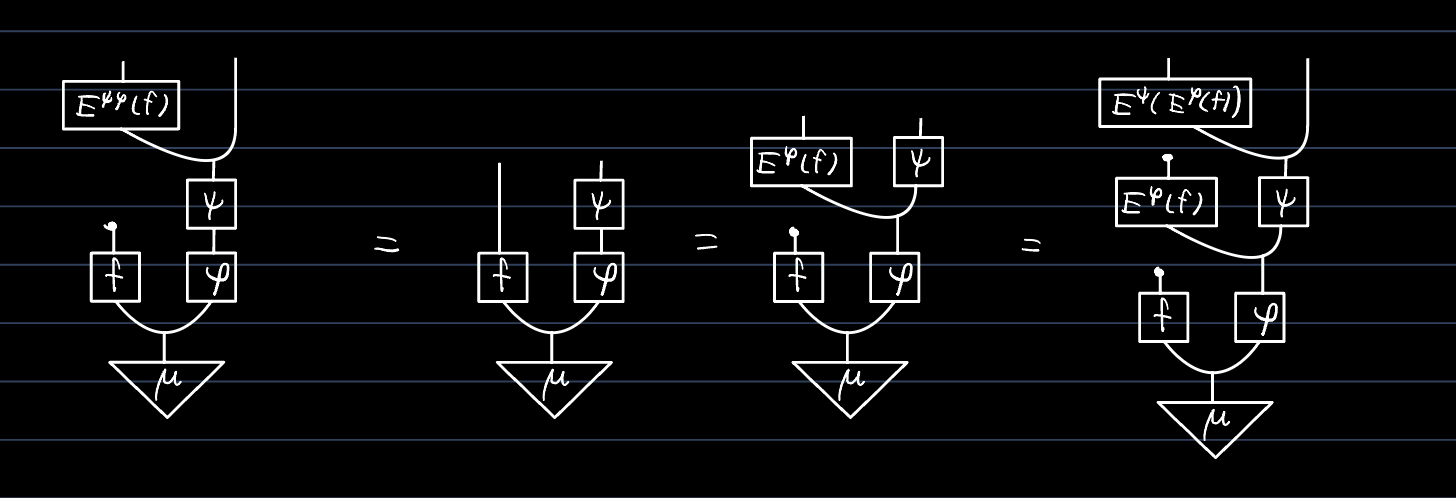
$E^\varphi(f)$はmodulo$\varphi\mu$-a.s.(F, Definition 13.1)で定まる.また,$\mu$-a.s.で等しい$\varphi,\varphi'\colon X\to Y$および$f,f'\colon X\to R$に対して$\varphi\mu$-a.s.で$E^\varphi(f)=E^{\varphi'}(f')$である.
$\varphi\colon X\to Y$, $\psi\colon Y \to Z$に対し,$E^{\psi\varphi}(f)=E^\psi(E^\varphi(f))$ ($\psi\varphi\mu$-a.s.) である.
以下$\C$はcausal(F, Definition 11.31)とする.このとき$\C$の確率空間の圏$\ProbStoch(\C)$ (F, Definition 13.8)が定義される.
regular object $R\in\C$と$(X,\mu)\in\ProbStoch(\C)$に対し,$E(X,\mu)=E_R(X,\mu):=\C(X,R)/\mu$とおく($/\mu$はmodulo $\mu$-a.s. equalとする).$E$は関手$\ProbStoch(\C)\to\mathsf{Set}$を定める.
regular objectsの部分圏
明らかに$I\in\C$はregularである.$\Reg(\C)$で$\C$のregular objectsからなる部分圏を表す.
$R,S\in\Reg(\C)\Rightarrow R\otimes S\in\Reg(\C)$.
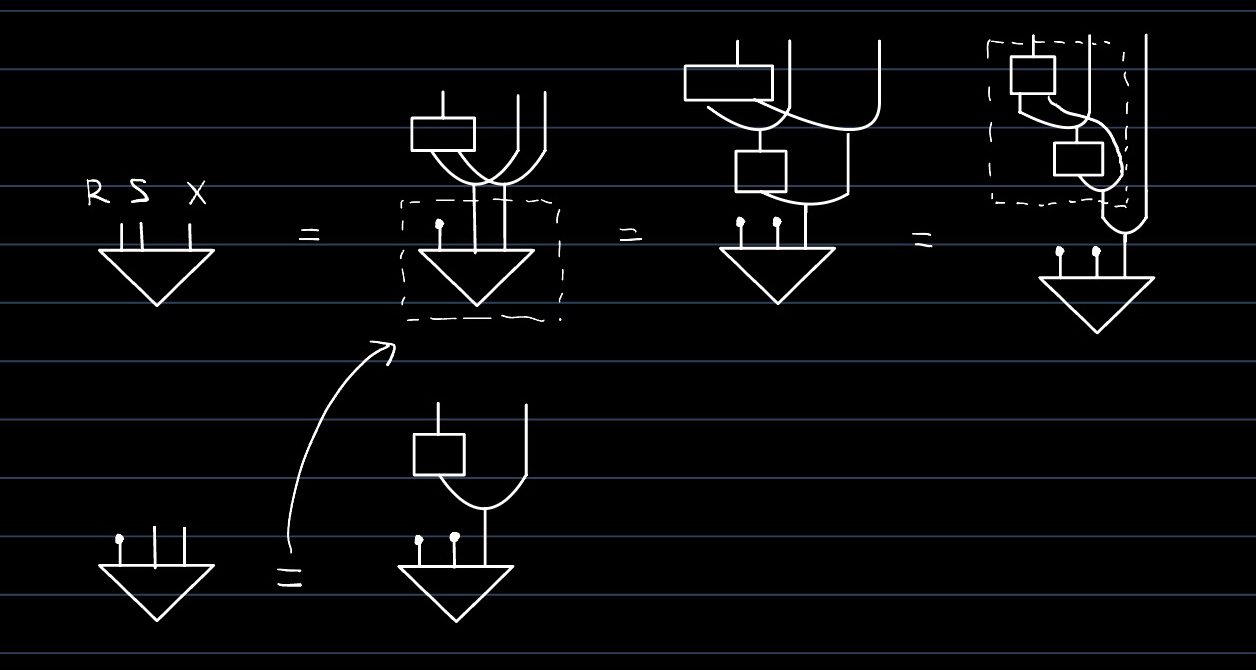
$\psi\colon I\to R\otimes X$がconditional distributionを持つことは,$\psi$ displays the conditional independence $I\perp'R\mid X$ ($\perp'$は縦棒が二本のやつの代わり,出し方わかんない,F, Definition 12.19) と同値であるから,補題はF, Proposition 12.20 (b) から直ちに従う.記事の証明は$A=I$の場合に書き直しただけである.
補題から,$\Reg(\C)$はマルコフ圏であって,またconditional distributionを持つ.
$(X,\mu)\in\ProbStoch(\C)$とする.$\Reg(\C)$の射$\theta\colon R\to S$はpost-compositionによって写像$\theta_{X,\mu}\colon E_R(X,\mu)\to E_S(X,\mu)$を定める.この対応によって関手$\Reg(\C)\to\mathsf{Set}$が定まる.
$\ProbStoch(\C)$の射$\varphi\colon(X,\mu)\to(Y,\nu)$および$\Reg(\C)$の射$\theta\colon R\to S$に対し,下図は可換である:
\begin{xy}\xymatrix{
E_R(X,\mu) \ar[r]^{\theta_{X,\mu}} \ar[d]_{E_R^\varphi} & E_S(X,\mu) \ar[d]^{E_S^\varphi}\\
E_R(Y,\nu) \ar[r]_{\theta_{Y,\nu}} & E_S(Y,\nu).\\
}\end{xy}
よって双関手$E\colon \Reg(\C)\times\ProbStoch(\C)\to\mathsf{Set}$を得る.
$\Stoch$における条件付き期待値
$\Stoch$を可測空間とマルコフ核のなすマルコフ圏とする.$[2]=\setex{0,1}\in\Stoch$を離散可測空間とする.$X\in\Stoch$に対し,射$f\colon X\to[2]$は,$f\mapsto f(\setex{1}\mid\mathchar`-)$により可測写像$X\to[0,1]$と1対1に対応する.
$[2]$はregularである.
より一般にstandard Borel(ポーランド空間の定めるボレル可測空間)はregularであるが一応証明する.
任意の可測空間$X$と$\mu\colon I\to[2]\otimes X$をとる.$\mu_i=\mu(\setex{i},\mathchar`-)$, $i=0,1$, とおき,$\mu$の周辺化を$\bar\mu=\mu_0+\mu_1$とおく.$\mu_i\ll\bar\mu$であるから,Radon-Nikodymにより$\mu_i=f_i\bar\mu$なる$X$上の非負値可測写像が存在する.$\bar\mu=(f_0+f_1)\bar\mu$であるから$\bar\mu$-a.s.で$f_0+f_1=1$である.よって$\Stoch$の射$f\colon X\to[2]$が$f(\setex{i}\mid x)=f_i(x)$ ($\bar\mu$-a.s.) によって定まる.($f_0(x)+f_1(x)\neq1$なる$x$については適当に値を置き換えればよい.) $f$は$\mu$のconditional distributionである.
$(X,\Sigma_X,\mu)$を確率空間,$\mathcal{F}\subset\Sigma_X$をsub$\sigma$-algebraとし,$\varphi$を可測写像$(X,\Sigma_X)\ni x\mapsto x\in(X,\mathcal{F})$に対応するマルコフ核とする.$\Stoch$の射$f\colon(X,\Sigma_X)\to[2]$に対し,$E^\varphi(f)$は通常の条件付き期待値$\mathbb{E}[f\mid\mathcal{F}]$に一致する(記号を濫用して$\Stoch$の射$X\to[2]$と可測写像$X\to[0,1]$を同一視している).