力学系と数理生物学

駒場理数サークルのアドカレ11日目の記事をご覧いただきありがとうございます。
初めまして、東京大学統合自然科学科４年のsfgです。
物理学、数学、生物等幅広い分野に興味を持っています。
さて、今回僕が書く記事のテーマは「力学系と数理生物学」です。
以下の記事では仮定する前提知識としては、簡単な微分方程式の知識のみで、生物に関する知識はほとんどなくて大丈夫です。
数理的なことに興味がある方、生物学に興味がある方、はたまた特に興味はないけどたまたまこの記事を開いてくださった方、全員が最後まで読めるよう、なるべく基礎的、それでいて興味深い内容で構成しました。
最後まで読んでくださると幸いです。

力学系とは何か

そもそもで皆さん「力学系」とは何だと思いますか。
多くの方は物理で習うような「力学」をイメージするかもしれません。もちろんその「力学」と関連がないわけではないのですが、ここでいう「力学系」とはもう少し広い概念です。
Wikipediaにおいて、力学系とは

力学系（りきがくけい、英語: dynamical system）とは、一定の規則に従って時間の経過とともに状態が変化するシステム（系）、あるいはそのシステムを記述するための数学的なモデルのことである。 https://ja.wikipedia.org/wiki/%E5%8A%9B%E5%AD%A6%E7%B3%BB

と述べられています。より純粋数学的に力学系の理論を扱いたい場合は、もう少し厳密に定義を確認するべきでしょうが、今回の話においてはこの程度の認識で十分です。

要はあるルールにしたがって時間発展する系について扱おう、という話が広い意味での「力学系の理論」だと思って差し支えありません。(以下では力学系を扱う理論のことも「力学系」と呼称することにします)

では、時間発展を記述する、といった場合何を思い浮かべますか？多くの方は「微分方程式」を思い浮かべるのではないでしょうか？
その考え方は良いと思います。ところが、微分方程式の講義等を取ったことがある人ならわかると思いますが、微分方程式って、見た目以上に解くのが難しいんですよね。
特に、生物に関わる現象を記述する微分方程式は、そもそも解析的に解けない(あるいは非常に困難)といった場合がほとんどです。
次の式をご覧ください。

$\begin{eqnarray} \left\{ \begin{array}{l} \frac{dp_1}{dt}=\frac{\alpha}{1+p^2_2}-p_1\\ \frac{dp_2}{dt}=\frac{\alpha}{1+p^2_1}-p_2 \end{array} \right. \end{eqnarray}$
こちらの連立微分方程式、非常に対称性のよい形をしていますね。
一見簡単に解けそうですが、これをきちんと解こうとすると非常に難しいです。
理由はシンプルで、非線形かつ連立な微分方程式になってしまっているからです。

ちなみにこちらは、以下のような生物現象を簡単にモデル化したものとなっています。

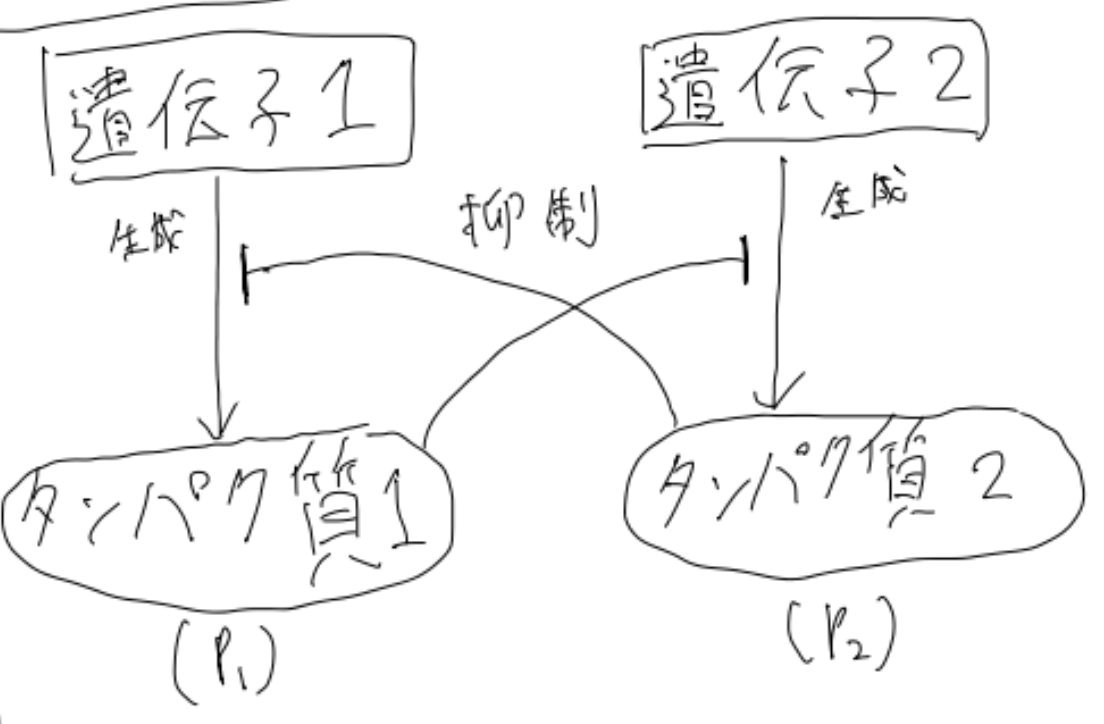
(手書きの図で見づらくてすみません)
こちらは「トグルスイッチ」と呼ばれるものです。簡単にいうと、タンパク質１がタンパク質２の、タンパク質２がタンパク質１の生成をそれぞれ抑制する、という系をモデル化したものです。

さて、話を数学に戻しましょう。
このような系が一体どんな振る舞いをするのか、それを知るのに微分方程式を実際に「解く」というのは実は不要です。
ではどのようにして、この系の振る舞いについて調べていくのか、そのことについて以下で詳しく述べていくこととします。

非線形微分方程式の定性的な扱い

ここからは、非線形な微分方程式を定性的に扱う方法について述べていきます。
「定性的」といっているのは、具体的にどのような解になるのかを考えるのではなく、解の挙動について分類していく、ということです。

１次元の場合。

相図とは何か

まずは１次元の場合について考えてみましょう。
$$ \frac{dx(t)}{dt}=\sin x(t) $$
このような微分方程式について考えます。
実はこの方程式は、解析的に解を求めることはそう難しくありません。いわゆる「変数分離」の形をしているので。(気になる方はChatGPT等のAIに聞いてみるとすぐ教えてくれると思います)
とはいえそのためには、積分を行う必要があるなど、多少面倒くさい計算が必要なのも事実です。
ここで「$t\rightarrow\infty$のとき$x$はどのような挙動をするのか」という問いを立てたとします。
要は十分時間が経過した後はどのような状態なのか、ということですね。
この問いに答えるのに、実際に解を求める必要はありません。
以下の図をご覧ください。

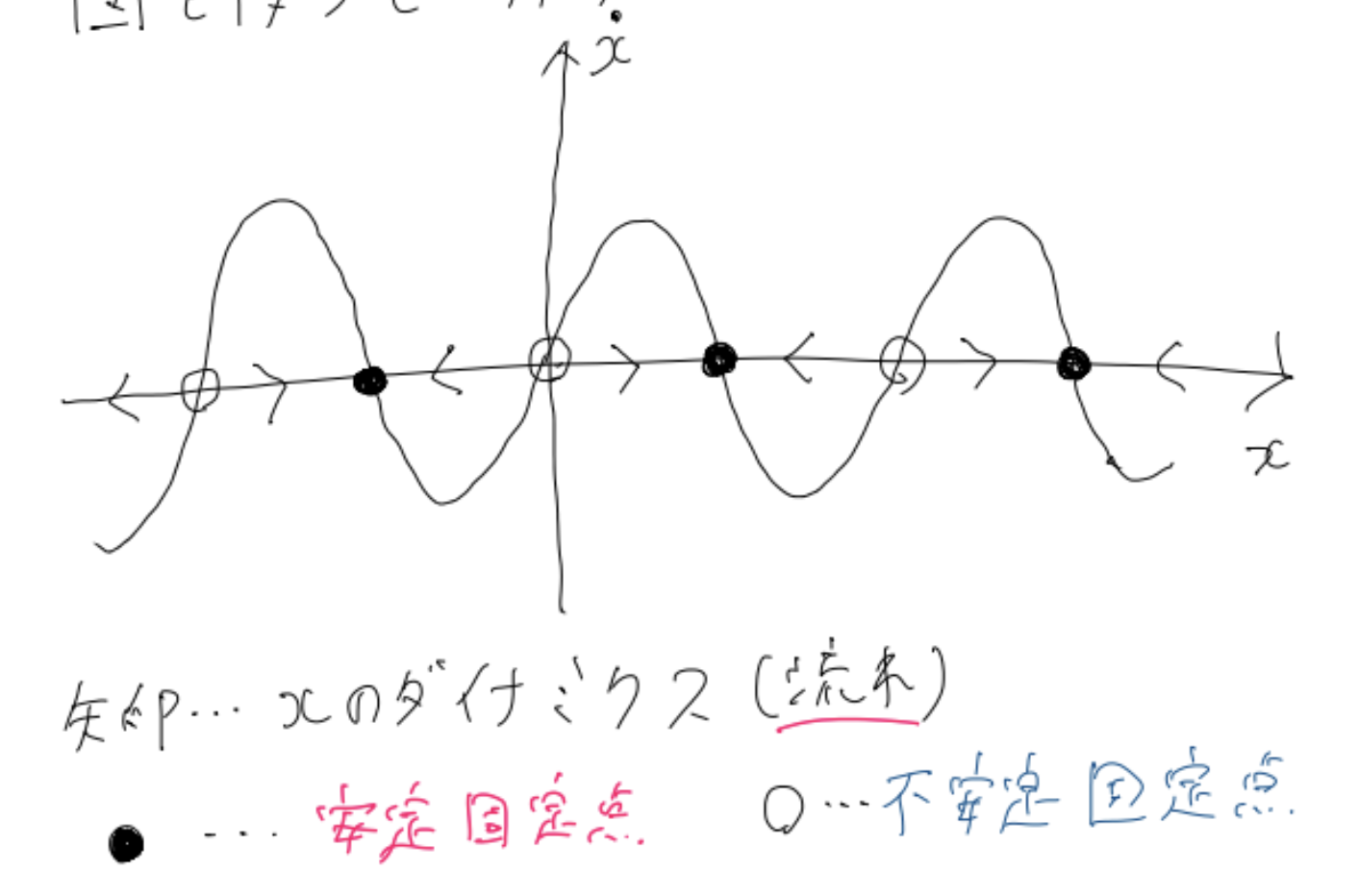
これは、横軸を$x$、縦軸をその時間微分$\dot{x}$、としたものです。
$\dot{x}$が正のとき$x$は増えようと、$\dot{x}$が負のとき$x$は減ろうとします。そのようなダイナミクス(流れ)を表したのが$x$軸上の矢印です。
これをみると一目瞭然。十分時間が経過した後に$x$は$x$軸上の黒丸で表される「安定固定点」に行き着きます。どの安定固定点に行き着くかは初期値次第ですね。
このような図を「相図」と呼びます。(相図と呼ばれるものは他にも多くありますが定性的な挙動がことなる「相」をわけた図として考えると、個体液体気体とうの相図と本質的に似通ったものだとわかりますね)
こうして、相図を描くことによって、その微分方程式の挙動が一目瞭然にわかります。
今回は簡単な図だったので手書きでしたが、もう少し複雑な場合だとコンピュータを使って図をプロットする、ということもありえます。

分岐

次にこの相図を用いることで、より明確にわかる「分岐」というものについて解説していきます。
簡単にいうと分岐とは、微分方程式に含まれるパラメータを変化させていくことで、その解の挙動が定性的に変化する、ということです。
百聞は一見にしかず、主な分岐について解説していきましょう。
まず一つ目は「サドルノード分岐」と呼ばれるものです。
$\dot{x}=r+x^2$
という非常にシンプルな微分方程式を考えます。(ここで$\dot{x}$は$\frac{dx(t)}{dt}$を表します。物理でよく使われる記法ですね)
この時、相図は以下のようになります。

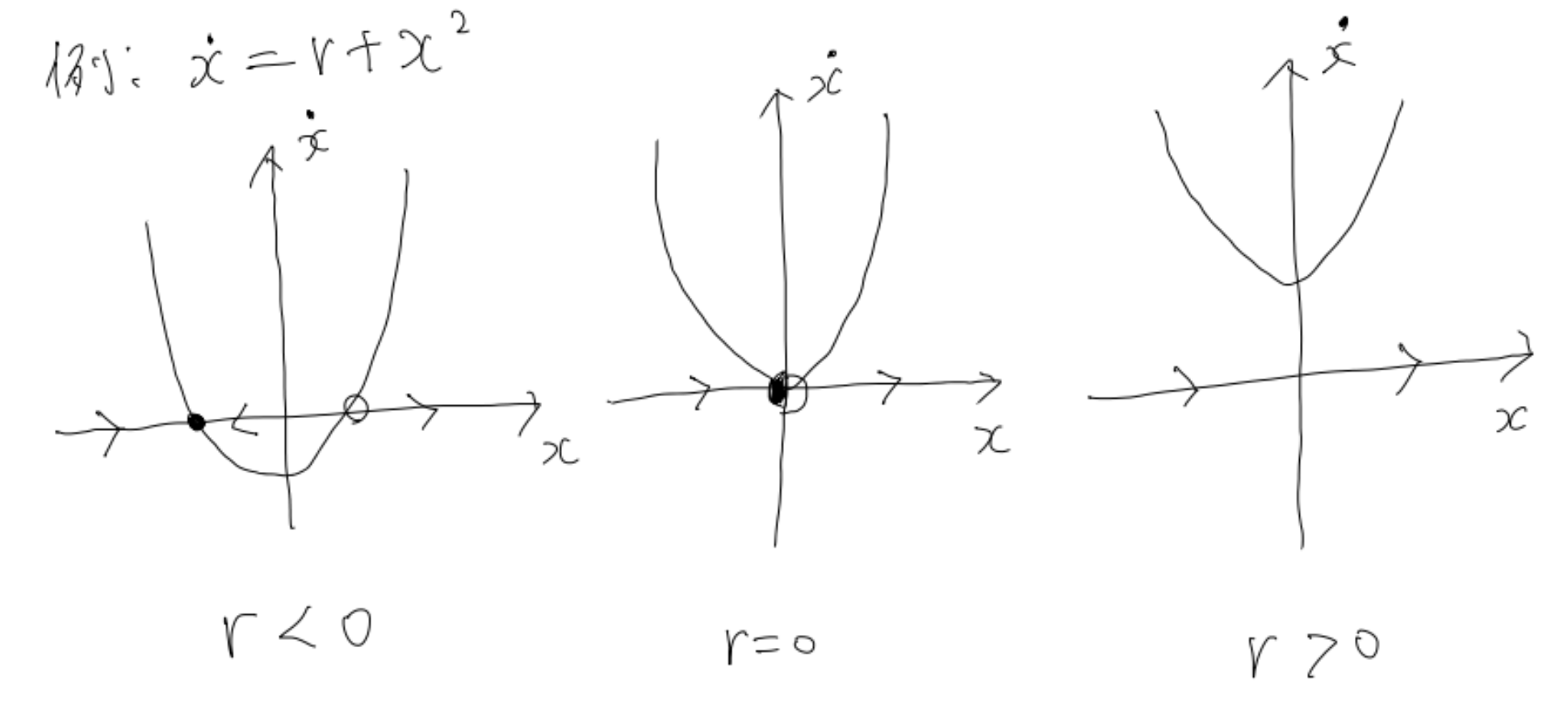
この図からも分かる通り、$r$が負のときは安定固定点が存在する一方、正になると消失し常に解は発散してしまいます。
もう少し具体的に述べましょう。
例えば初期値が同じ$x(0)=0$であっても、$r<0$なら、十分時間が経った後には$x=-\sqrt{|r|}$という安定固定点に行き着く一方、$r>0$の場合は正の無限大に発散してしまいます。
他にも以下のような分岐が存在します。


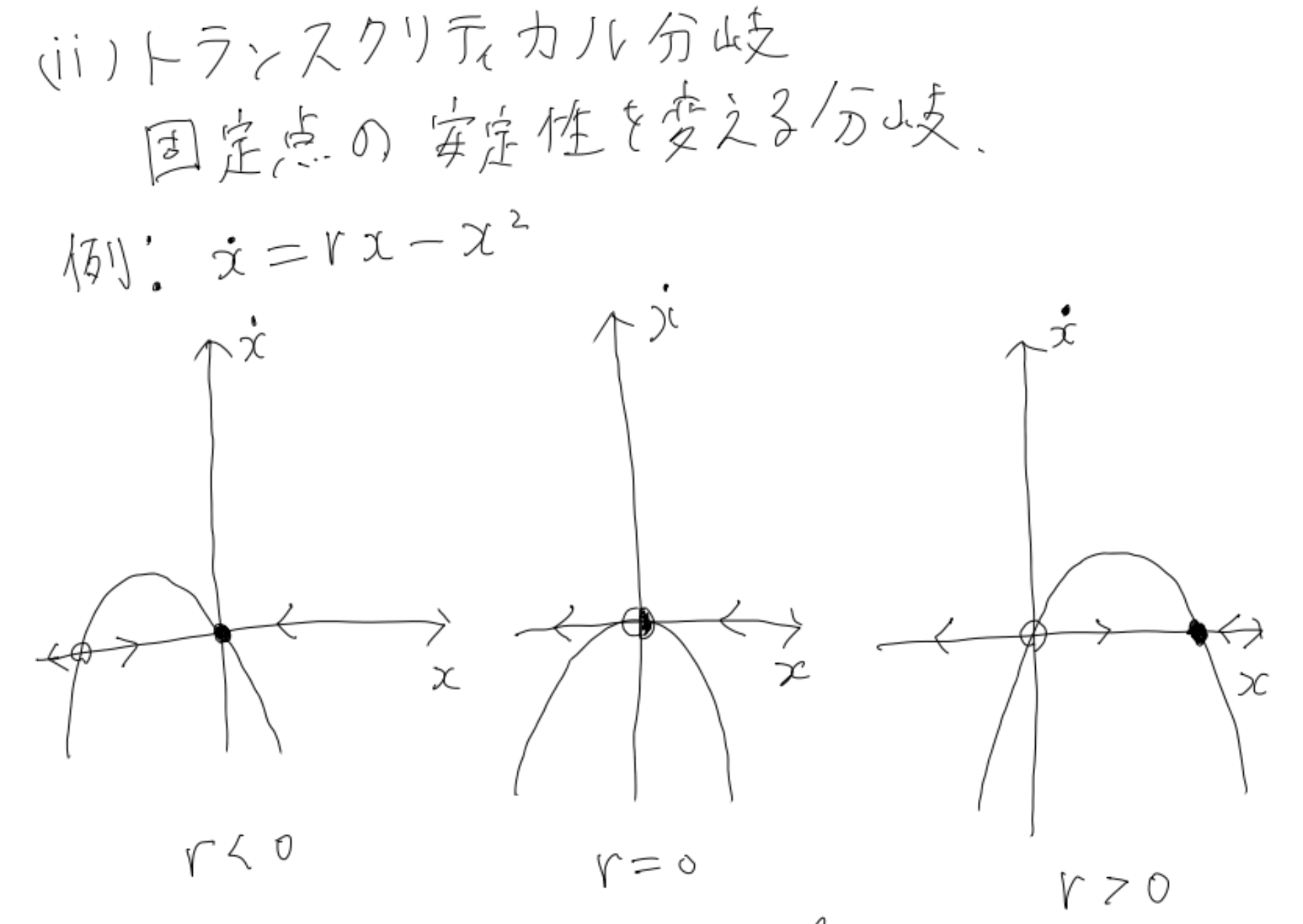
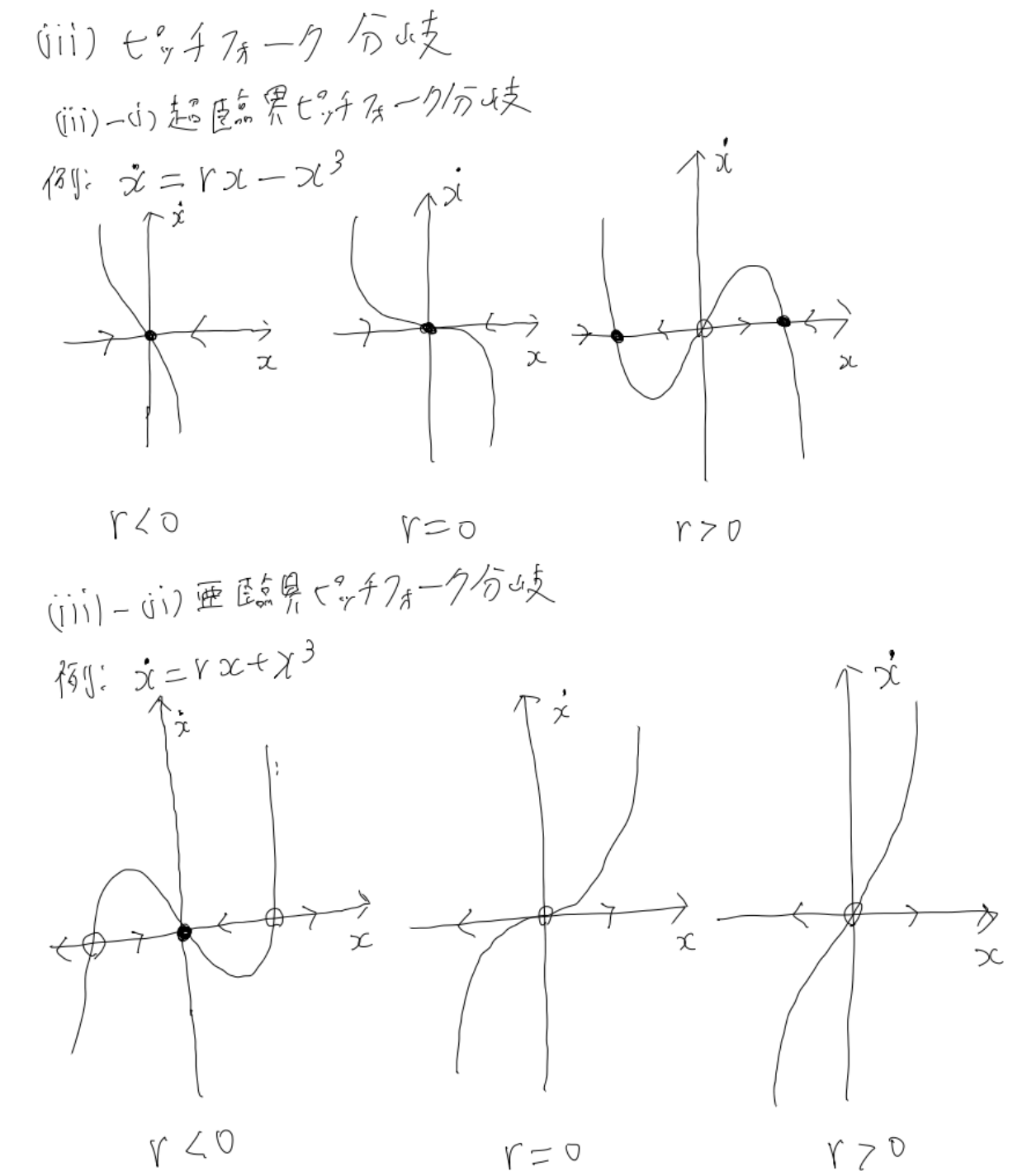
超臨界ピッチフォーク分岐なんかは、物理をやっている人だと相転移らへんで見たことがあるのではないでしょうか？
このように、パラメータを変化させることで系の定性的な挙動がガラッと変化することがあります。

生物への応用

それではこれらを実際に生命現象に応用していきましょう。この記事の「数理生物学」の部分です。
ここでは昆虫の個体数の変化について考えます。個体数を$N$とすると、その時間変化をモデル化した微分方程式として以下のようなものを挙げることができます。

$\dot{N}=RN(1-\frac{N}{K})-\frac{BN^2}{A^2+N^2}$

ここで$R$は増殖率(要はどれだけ子供が生まれるかのような指標)、$K$は環境収容力(要は個体数がこれを超えると減少しようとする指標)です。
また、第２項は捕食による影響を入れたものです。
物理をやったことがある人間なら馴染みがあるかと思いますが、この挙動をより見やすくするために出てくる物理量を全て無次元化します。
すると、上記の微分方程式は

$\frac{dx}{d\tau}=rx(1-\frac{x}{k})-\frac{x^2}{1+x^2}$

となります。それぞれ小文字になった部分は、元の大文字の部分を無次元化したものです。
この系の固定点つまり時間微分が０になるような値$x^*$は$x^*=0$と、$r(1-\frac{x^*}{k})=\frac{x^*}{1+x^{*2}}$の解です。

相図を描くと以下のようになります。(ただし右辺の正負をそのまま考えるのではなく、右辺を二つの関数に分けその上下関係で考えます)

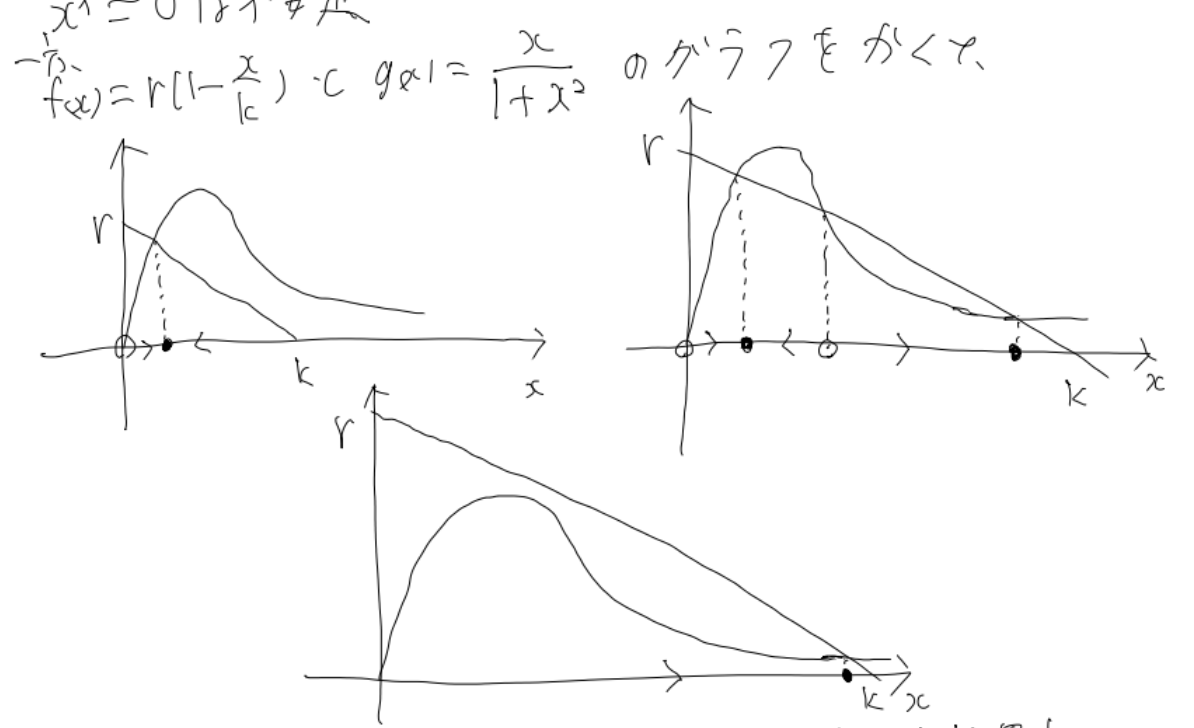
ここで3つの相図は、$r$をある程度大きい値で固定した上で、$k$を増やしていくとどうなるのかを表した図です。(具体的には左上、右上、真ん中、の順番です)

サドルノード分岐が２回起こっているのが分かるでしょうか？
具体的には、もともと一つしかなかった安定固定点が、2つに増えたのちに、元々あった安定固定点が消失しているのです。

さて、これによって昆虫の大発生を説明することができます。
まず、元々そこまで環境収容力が大きくなかったとしましょう。この場合は左上の相図の状態に相当します。この時、系は十分時間が経った後だとすると、個体数は固定点における値を取ると考えることができます。
そこから何らかの影響で環境収容率が上昇し、今現在いる安定固定点が消失し、十分大きい方の安定固定点のみが存在する、真ん中の相図の状態になったとします。
すると、個体数は、消失した固定点の代わりに新たに生じた安定固定点に行きつこうと爆発的の増加するのです。

いかがでしょうか。
このように、解析的に解くことが困難な微分方程式を、相図を用いて扱うことにより、個体数の爆発的な増加という生命現象を数理的に扱うことができました。
もちろん、現実の生命現象をこのようなシンプルなモデルのみで考えることが適切かと言われると怪しくはあります。
ですが、環境が少し変化するだけでも、個体数が爆発的に増える、という現象を理論的にこのようにして説明できる、ということは、現象の本質を抜き出してモデル化する「物理学」として大成功である、と僕は思います。

ただこの１次元の議論だけでは、冒頭にあげたトグルスイッチについて考えることはできません。
それでは次に２次元の話について考えてみましょう。

２次元の場合

２次元の場合でも相図を書いて考えることができますが1次元と2次元以上では違いがいくつかあります。
特に重要な相違点として挙げられるのは、固定点付近での挙動を分類することができる、という点です。
以下では、線形の場合について議論します。
これは、非線形の場合は議論することができない、というわけではありません。もし非線形な連立微分方程式について考えたい場合は、固定点周りでテイラー展開を行うことで微分方程式を線形化し、着目したい固定点周囲での挙動を考えることができます。あるいは、数値的にプロットを行うことで大域的な挙動を見ることも可能です。

相図による固定点の分類

まず「サドル」と呼ばれる固定点を、具体的な方程式とともに説明します。
$ \begin{eqnarray} \left\{ \begin{array}{l} \dot{x}=x+y \\ \dot{y}=4x-2y \end{array} \right. \end{eqnarray} $
このような方程式は$\boldsymbol{x}= \begin{pmatrix} x \\ y \end{pmatrix},A= \begin{eqnarray} \left( \begin{array}{cc} 1 & 1 \\ 4 & -2 \end{array} \right) \end{eqnarray} $
を用いると
$$ \dot{\boldsymbol{x}}=A\boldsymbol{x} $$
と書くことができます。
このとき一般解は、$A$の固有ベクトルを用いることで、
$$ \begin{eqnarray} \left( \begin{array}{cc} x \\ y \end{array} \right) ＝c_1e^{2t} \left( \begin{array}{cc} 1 \\ 1 \end{array} \right) +c_2e^{-3t} \left( \begin{array}{cc} 1 \\ -4 \end{array} \right) \end{eqnarray} $$
と書くことができます。（但し$c_1,c_2$は定数）
実際に方程式に代入することで確かめることもできます。

そしてこの方程式の相図を書くと、以下のようになります。

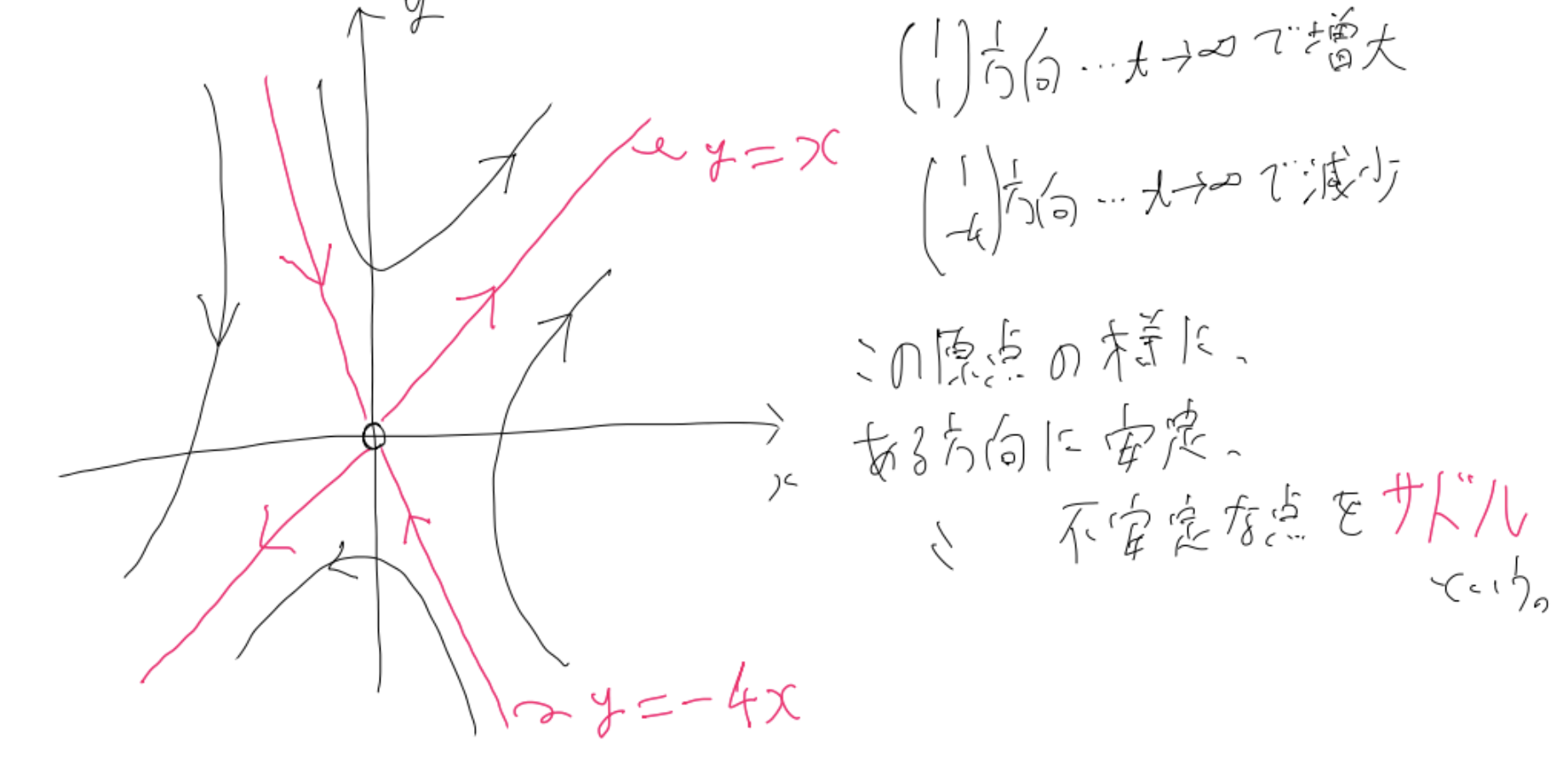
この図からも分かる通り、$A$の固有値が正の方向には固定点から離れるような、負の方向には固定点に近づくような挙動をします。
他の場合の相図についても以下に掲載します。($\lambda$は固有値のこと)

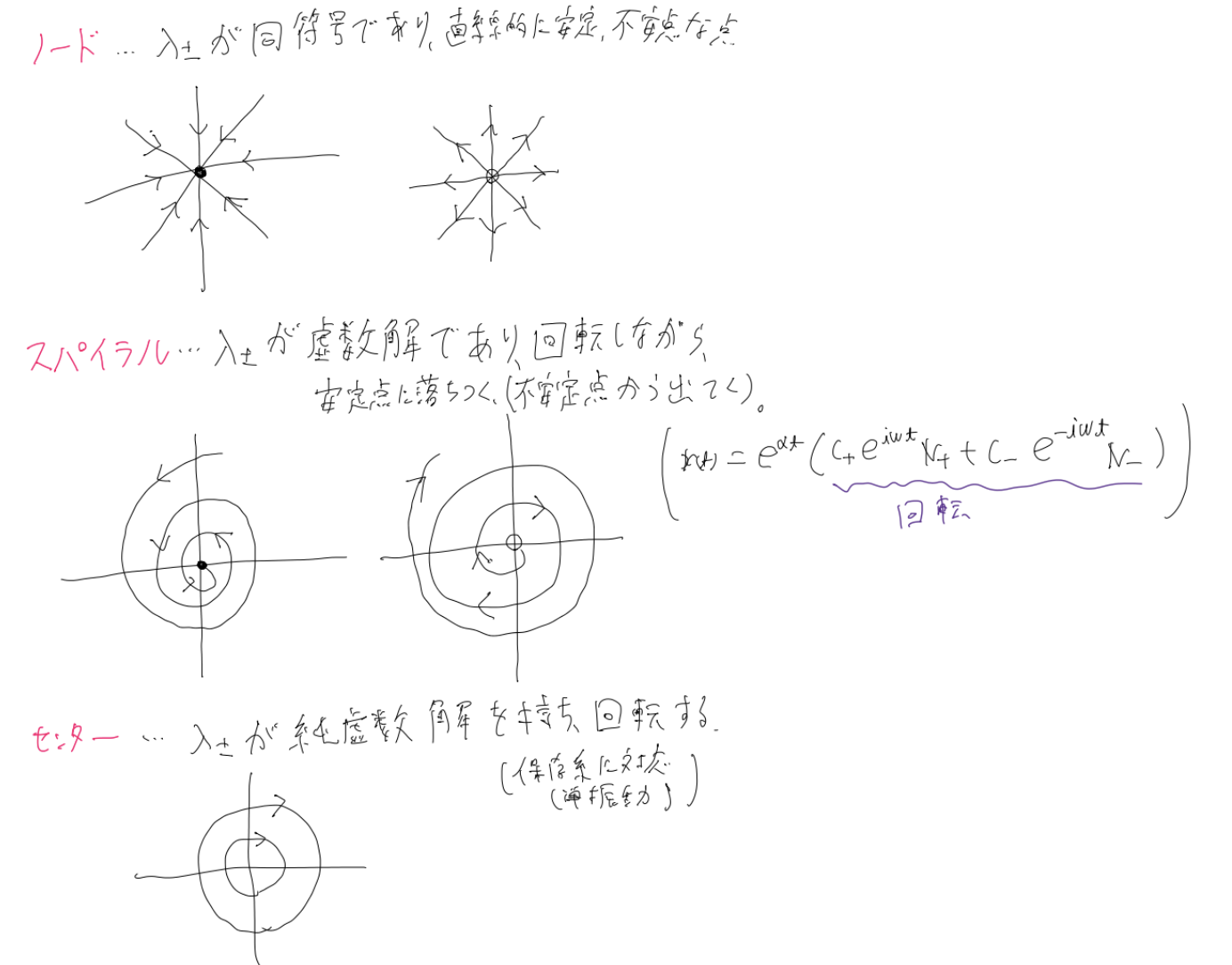
これらの図から分かる通り、微分方程式を線形化したときの行列の固有値によって、固定点を分類することができるのです。
また、$\dot{x}=0$や$\dot{y}=0$を満たす曲線を「ヌルクライン」と呼び、それらを図示することでも、微分方程式の解の定性的な挙動について考えることができます。

このヌルクラインを用いた方法を、最初に挙げた「トグルスイッチ」の例を用いて紹介しましょう。
再びその系の微分方程式を以下に記します。
$\begin{eqnarray} \left\{ \begin{array}{l} \frac{dp_1}{dt}=\frac{\alpha}{1+p^2_2}-p_1\\ \frac{dp_2}{dt}=\frac{\alpha}{1+p^2_1}-p_2 \end{array} \right. \end{eqnarray}$
そして、この系のヌルクライン、および挙動を図示したものが、以下の図です。

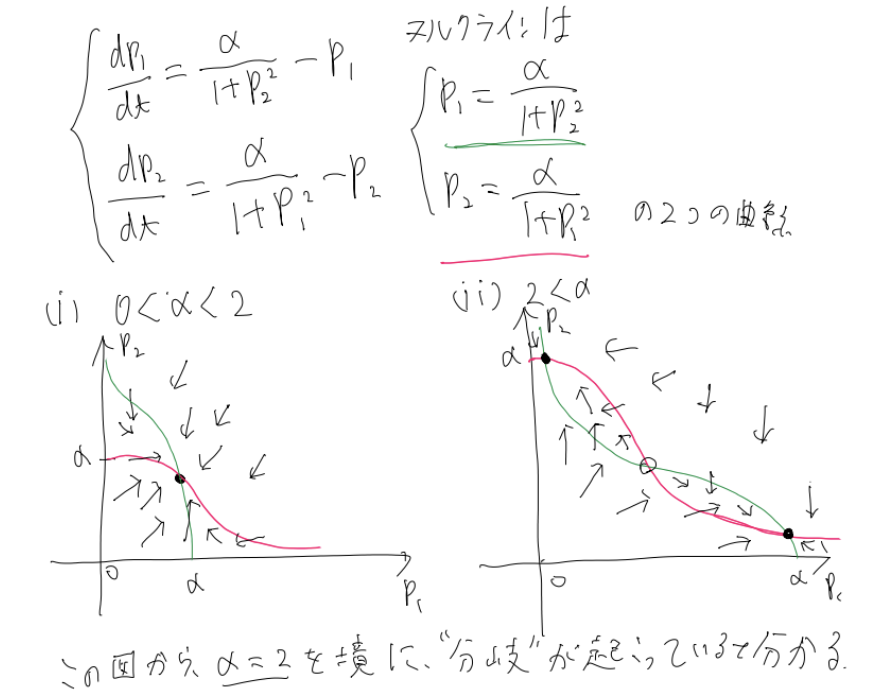
この図から分かる通り、$\alpha$というパラメータの値に応じて、2つのタンパク質が同じくらい生成されているか、あるいは片方が多く生成されているか、という状態が変化しています。
このようにして、生体内のダイナミクスについても数理的に解析することができるのです。

おわりに

いかがでしたでしょうか？
今回扱ったような力学系の理論を用いることで、複雑な式で記述される生命現象についても、理解することができます。
もちろん今回紹介したのは、力学系の理論の一部であり、他にも非線形な微分方程式を扱う方法はいくつもあります。
また、カオスなどといった面白い挙動も、生命現象の理解には重要な要素の1つです。
是非この記事を読んだことをきっかけとして、貴方も数理生物学をより詳しく学んでみませんか？？