ガウスの消去法の幾何的解釈

はじめに

線形代数の最初のゴールである連立方程式の解は，幾何的には複数の直線（一般には超平面）の交点であることは有名かと思います．

では，その解法であるガウスの消去法は，幾何的にはどんな操作をしているのでしょうか？「きっと誰かは解説しているだろう」と思い，
googleで画像を検索してみたのですが，意外にもそれらしい絵は見つかりませんでした．

そこで，本記事では，ガウスの消去法を幾何的に解釈してみることにしました．普段は数値的にしか扱わないガウスの消去法に新しい解釈を加えることで，より深く理解する手助けにもなると思います．

なお，本記事では簡単のために，2変数の場合を扱いますが，$n$変数の場合にも容易に拡張できます．

ガウスの消去法

まずは，ガウスの消去法を復習しましょう．ガウスの消去法は，一言でいえば，「式を足し引きして，変数を消していく」アルゴリズムです．詳細はこちら[1]を参照ください．本記事では，アルゴリズムの挙動の例を一つ見てみます．

以下の問題を扱います．

\begin{align} f_1(x, y) = 2 x + y - 3 = 0 \\ f_2(x, y) = x + 2 y - 3 = 0 \end{align}

行列表記すると以下になります．

\begin{align} \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 3 \end{pmatrix} \end{align}

まずは，式$f_2$から変数$x$を消してみましょう．式$f_1$を$1/2$倍して，式$f_2$から引いてみます：$f_2(x, y) - 0.5 f_1(x, y) = 0$．

\begin{align} \begin{pmatrix} 2 & 1 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 3/2 \end{pmatrix} \end{align}

次に，式$f_1$から変数$y$を消してみましょう．式$f_2$を$2/3$倍して，式$f_1$から引いてみます：$f_1(x, y) - 2/3 f_2(x, y) = 0$．

\begin{align} \begin{pmatrix} 2 & 0 \\ 0 & 3/2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 3/2 \end{pmatrix} \end{align}

最後に，係数を1に直して終わりです．

\begin{align} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{align}

解は$x = 1, y = 1$となりました．

幾何的解釈

では，ガウスの消去法を幾何的に解釈してみましょう．

まずは，連立方程式の絵を描いてみます．表示しているベクトルは各直線に対応している行ベクトルで，これは各直線に垂直なベクトル（法線ベクトル）となります．

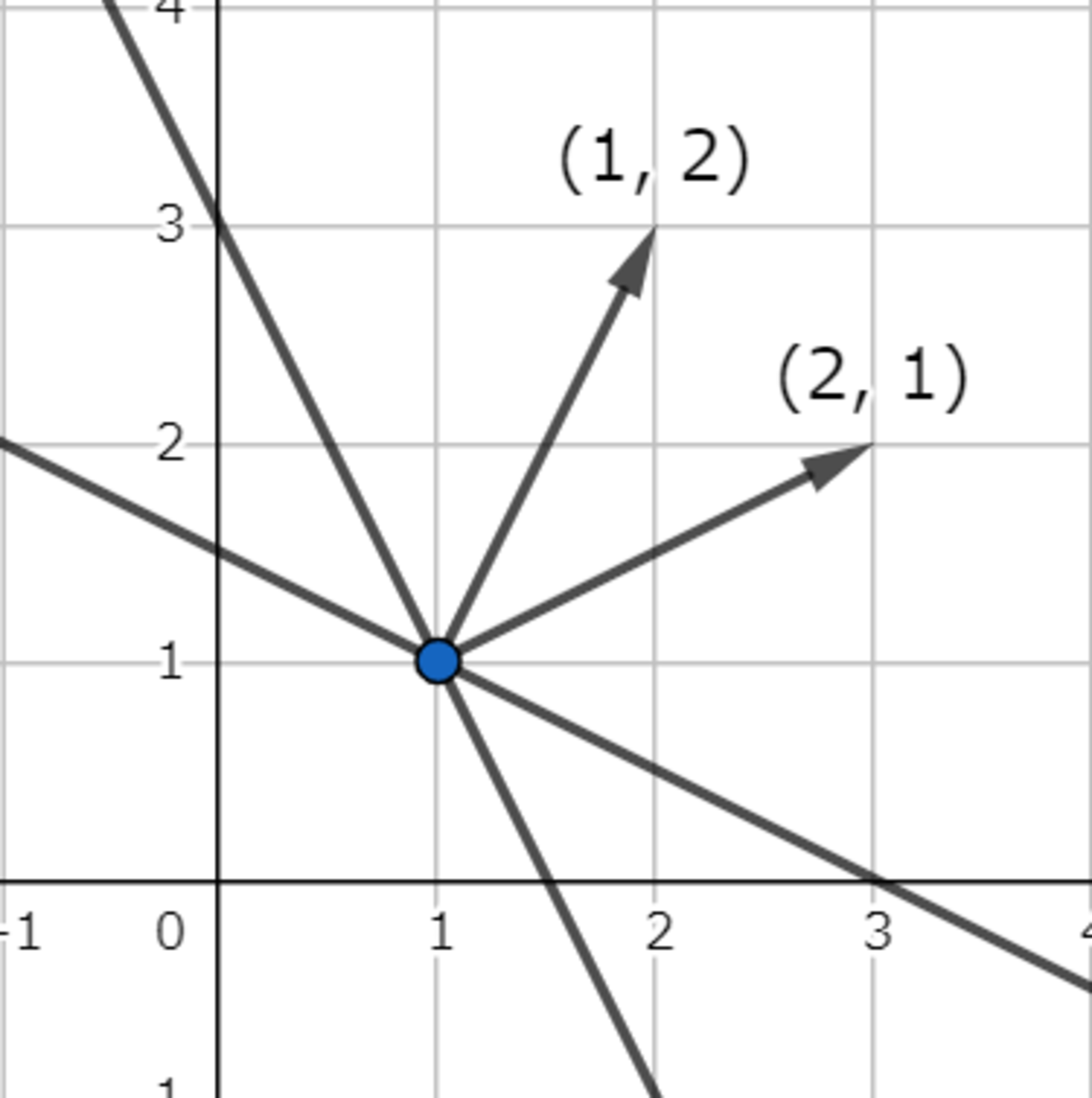連立方程式の解

では，ガウスの消去法における「式の足し引き」は何を意味するのでしょうか？これは，「二つの直線の交点を通ったまま，直線を回転させること」に相当します．一般に，二つの直線$f_1, f_2$に対して，実数$k$を用いて表される直線$f(x, y) = k f_1(x, y) + f_2(x, y) = 0$は，二つの直線$f_1, f_2$の交点を通ることが知られています[2]．これは，高校数学での「二つの直線の交点を通る直線」に相当します．以下の図では，$k$の値をいくつか変えたときの直線を示しています．いずれも元々の二つの直線の交点を通っていることが分かります．

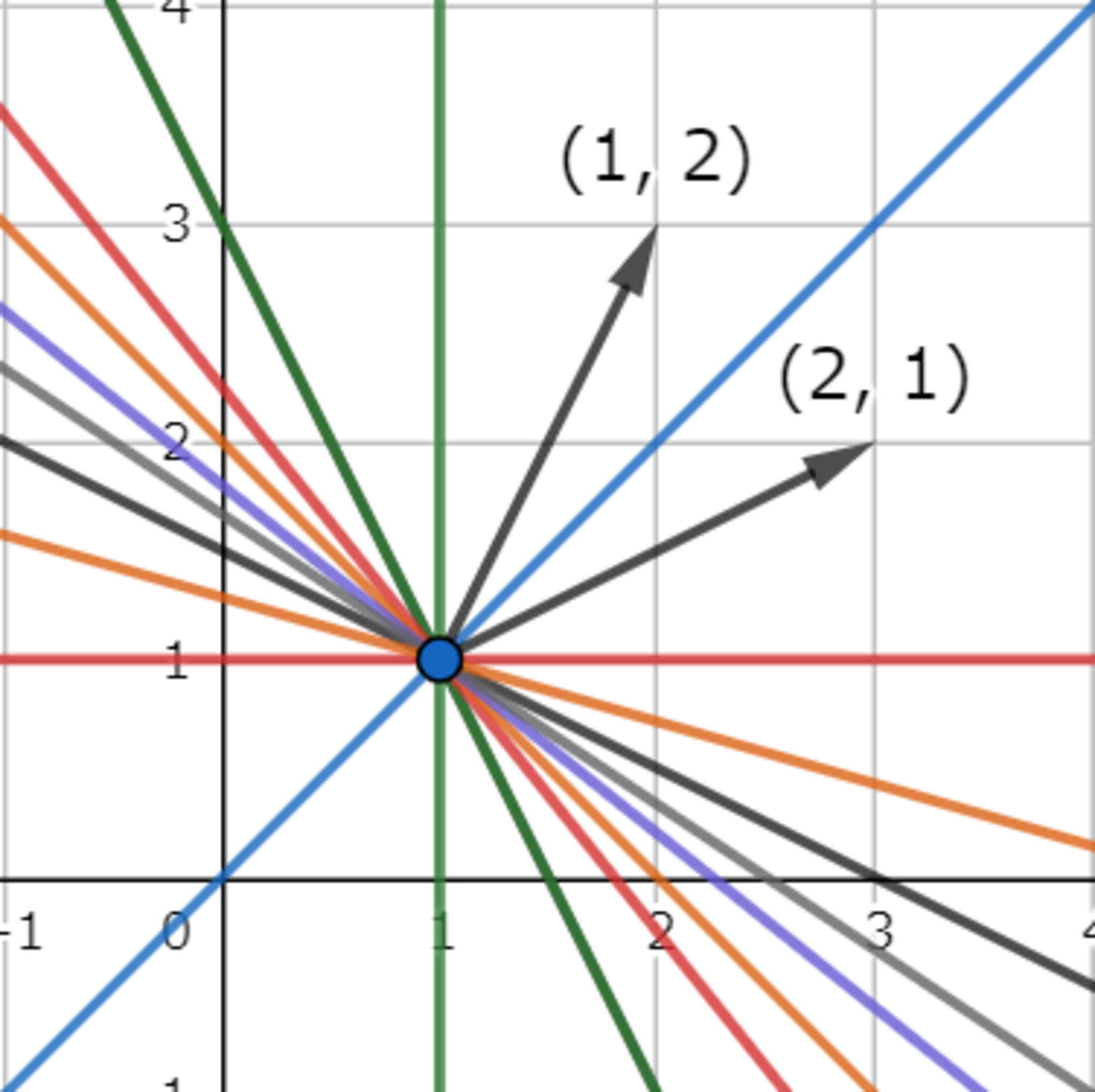二つの直線の交点を通る直線

では，「変数を減らす」は何を意味するのでしょうか？これは，「x軸／y軸と平行になるように直線を回転させること」に相当します．なぜなら，変数が減ると，その変数に対応する軸と法線ベクトルが垂直になり，一方で，その法線ベクトルに対応する直線が軸と平行になるからです．

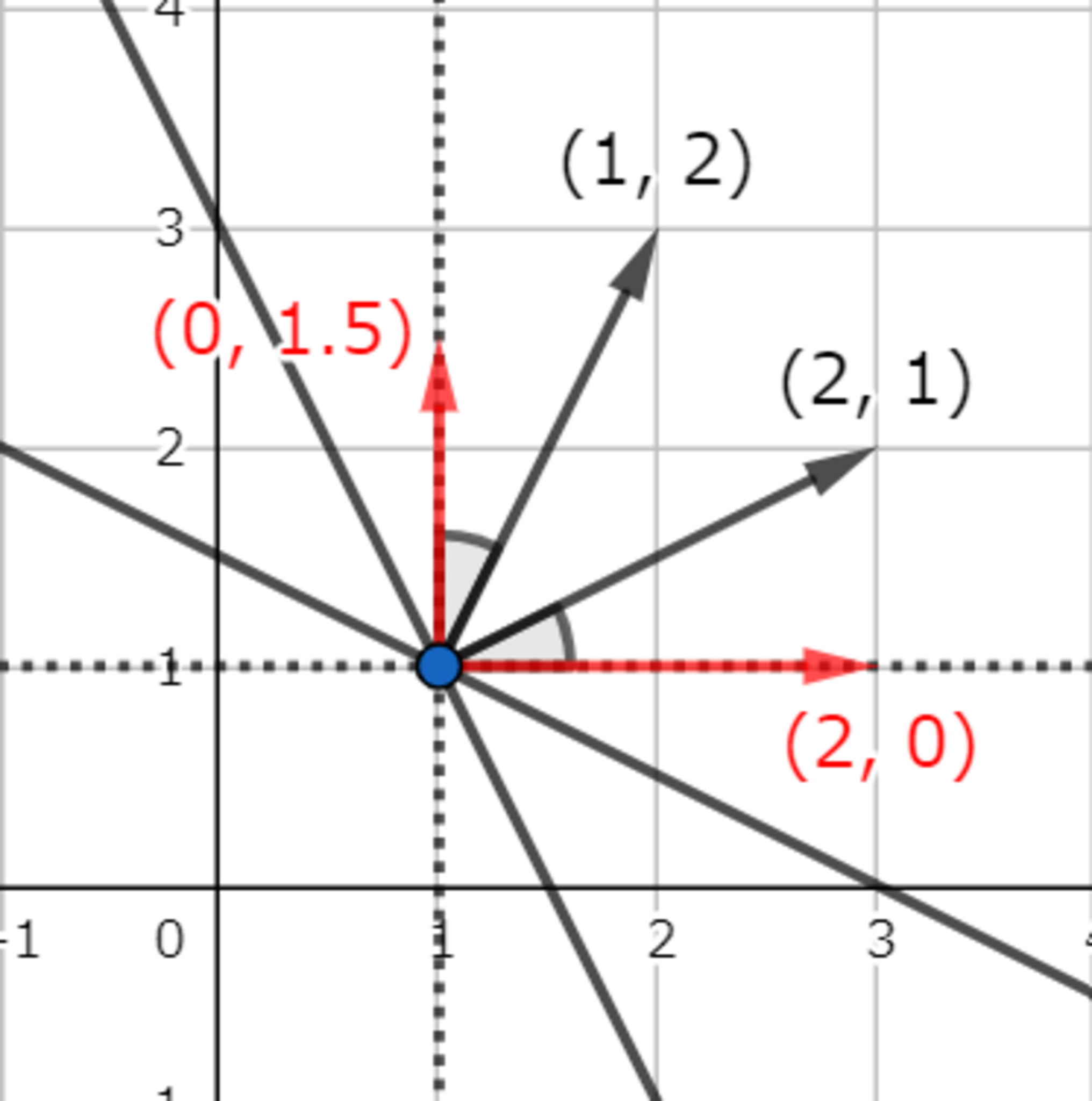変数を減らす操作

式の足し引きによる法線ベクトルの移動は，式に対応する法線ベクトルの足し引きですので，図で表現できます．以下の図でガウスの消去法の各ステップの動きを見てみましょう．

まず，直線$f_2$の法線ベクトル$(1, 2)$は，直線$f_1$の法線ベクトル$(2, 1)$を$-1/2$倍した分だけ移動させると，y軸と平行になります．

直線$f_2$の回転

次に，直線$f_1$の法線ベクトル$(2, 1)$は，直線$f_2$の法線ベクトル$(0, 3/2)$を$-2/3$倍した分だけ移動させると，x軸と平行になります．

直線$f_1$の回転

最後に，各法線ベクトルを正の値の単位ベクトルに直して終わりです．

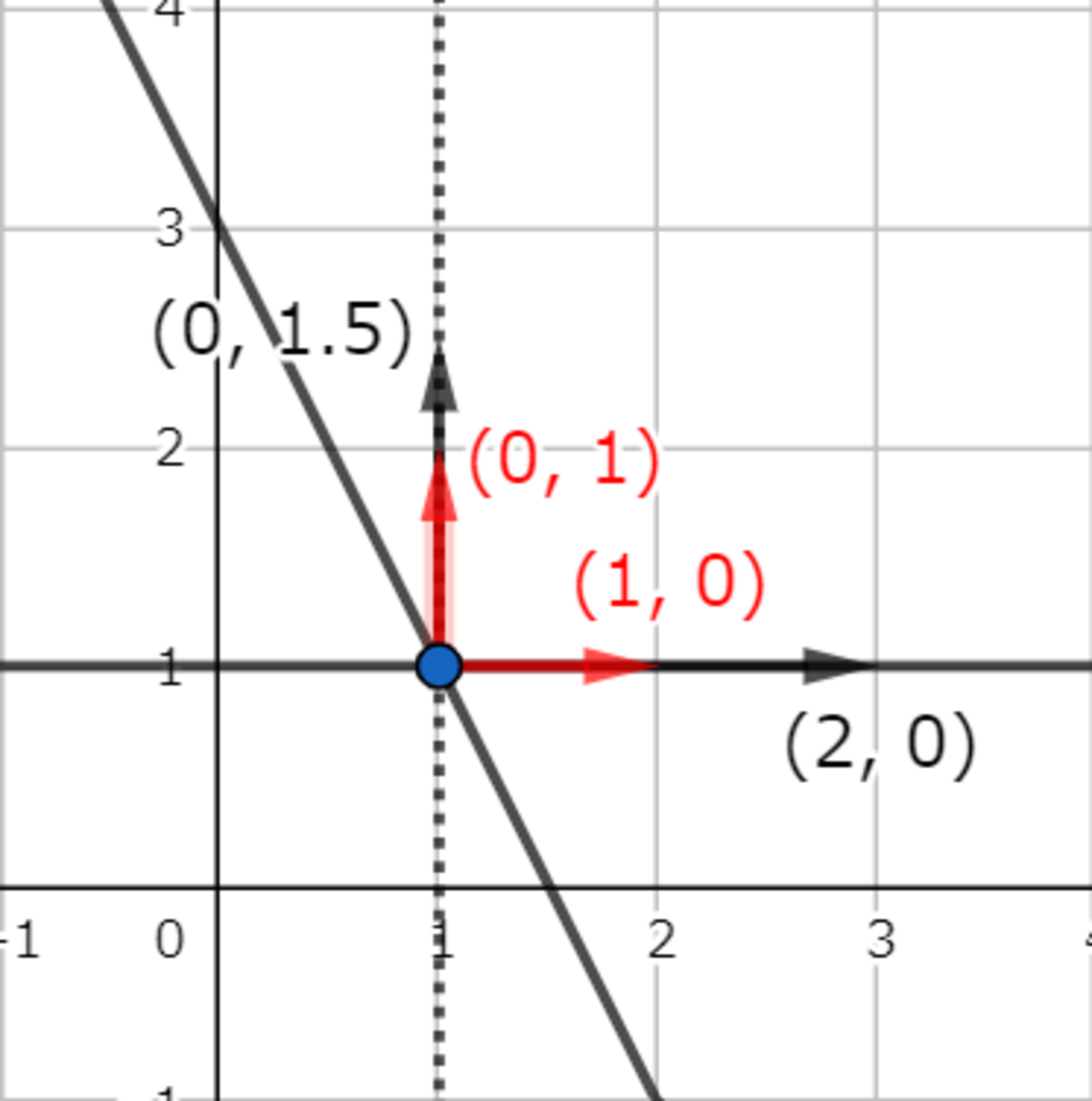ベクトルの正規化

このように，直線がx軸／y軸と平行になれば，$b$の値を見るだけで解が分かります．

おわりに

本記事では，ガウスの消去法の幾何的な解釈を紹介し，ガウスの消去法が「交点を通ったまま直線を回転させて軸と平行にすることで自明な解を持つ問題に変換する」アルゴリズムだと理解できるようになりました．

記事を書いていて，式の足し引きが交点を通ったまま直線を回転させる操作だと気づいたとき，こんなことも理解せずに使っていたのか，と正直自分に落胆してしまいました．今後も幾何的解釈を通して理解を深めていきたいです．