文献あり

「写像は二項関係の特殊なもの」という考え方によるwell-definedの解釈

3214

この記事では商集合上の写像を定義するときに出てくるwell-defined性に解釈を与えます。
「写像は二項関係の特殊なもの」という考え方を使い、商集合上の写像の定義がwell-definedであることを「写像であると期待して定義したものを二項関係として見て、それが写像である」という解釈を与えます。
「写像は二項関係の特殊なもの」という考え方では、二項関係のうち左全域性と右一意性を満たすものを写像といいます。well-defined性を考える上では右一意性が重要になります。

well-definedとは

なにか写像を定義したとします。その定義には問題があって、写像だと思って定義したものが実は写像ではなかった、ということがあります。そういうときに定義がwell-definedでないと言います。
逆に写像だと思って定義したものが確かに写像である場合（問題がない場合）、定義がwell-definedであるといいます。ここでは、商集合上の写像のwell-defined性について例を用いて説明します。まずは例のための準備をします。

準備

$Z$ 上の同値関係 $\sim$ を $x \sim y ⟺ x \equiv y (\mod 3) (x, y \in Z)$ と定義します。
同値関係 $\sim$ に関する $a \in Z$ の同値類を $[a] = {x \in Z ∣ x \sim a}$ と定義します（ $a$ を代表元と呼びます）。
$Z$ の同値関係 $\sim$ による商集合を $Z / \sim = {[a] ∣ a \in Z}$ と定義します。

次の式が成り立ちます。

$\dots = [- 6] = [- 3] = [0] = [3] = [6] = \dots$
$\dots = [- 5] = [- 2] = [1] = [4] = [7] = \dots$
$\dots = [- 4] = [- 1] = [2] = [5] = [8] = \dots$

また、 $Z / \sim = {[0], [1], [2]}$ と書けます。

この $Z / \sim$ のことを $Z / 3 Z$ と書くことが多いですが、ここではそのまま $Z / \sim$ を使います。

well-definedでない例

まずはwell-definedでない写像の定義の例を見てみます。

$f_{1} : Z / \sim \to Z / \sim; [a] \mapsto [| a |] (a \in Z)$ について考えます。結論から言うと $f_{1}$ は写像ではなく、 $f_{1}$ を写像だと思うと次のような問題が発生します。

次の式が成り立ちます。

$[1] = [- 2]$
$f_{1} ([1]) \neq f_{1} ([- 2])$ （ $f_{1} ([1]) = [1], f_{1} ([- 2]) = [2]$ で、 $[1] \neq [2]$ なので）

ここで、 $[1] = [- 2]$ なのに、 $f_{1} ([1]) \neq f_{1} ([- 2])$ であるという問題が発生しています。

このことから、 $f_{1}$ は写像ではない（写像の定義として問題がある）と言えます。

そもそも写像というのは、直感的に言うと「定義域の各元に対して、値域の元をひとつ定める対応」です。今回の場合は、定義域の元 $[1] = [- 2]$ に対して、2つの異なる元 $[1], [2]$ が対応してしまっているので写像ではない、と言えます。

このように、写像だと思って定義しようとしたけど、うっかり定義域のある元に対して値域の元を2つ以上定めてしまい、写像だと思ってたものが実は写像ではなかったというとき、写像の定義がwell-definedでないと言います。

今回の場合は
(1) 「ある $a_{1}, a_{2} \in Z$ が存在して、 $[a_{1}] = [a_{2}]$ だが $[| a_{1} |] \neq [| a_{2} |]$ 」
が成り立つ(例: $a_{1} = 1, a_{2} = - 2)$ からwell-definedでないと言えます。
また別の言い方をすると、同じ同値類でも代表元のとり方( $a_{1} = 1, a_{2} = - 2)$ によって計算結果( $f_{1}$ の出力)が異なるからwell-definedでない、という言い方もできます。

well-definedな例

$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ について考えます（これは $Z / \sim$ 上の足し算です）。

$f_{2}$ は本当に写像（定義がwell-defined）なのでしょうか。つまり、定義域の各元に対して、値域の元をひとつ定めているのでしょうか。

命題(1)と同じ考え方で
(2) 「ある $a_{1}, b_{1}, a_{2}, b_{2} \in Z$ が存在して、 $([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ だが $[a_{1} + b_{1}] \neq [a_{2} + b_{2}]$ 」
が成り立った場合には、定義域のある元に対して異なる2つの元を対応させてしまっているので写像では無い(well-definedではない)ことになってしまいます。
ただし、命題(2)は成り立たず、命題(2)を否定した次の命題(3)が成り立ちます。

(3) 「任意の $a_{1}, b_{1}, a_{2}, b_{2} \in Z$ に対して、 $([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ ならば $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ 」

余談:命題(3)が成り立つことの証明

証明

$[a_{1}] = [a_{2}]$ から、 $a_{1} \equiv a_{2} (\mod 3)$ が成り立ちます。
また、 $[b_{1}] = [b_{2}]$ から、 $b_{1} \equiv b_{2} (\mod 3)$ が成り立ちます。
$a_{1} \equiv a_{2} (\mod 3)$ と $b_{1} \equiv b_{2} (\mod 3)$ から、 $a_{1} + b_{1} \equiv b_{1} + b_{2} (\mod 3)$ が成り立ちます。
つまり、 $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ が成り立ちます。

命題(3)は $f_{2}$ の出力が代表元のとり方によらずに定まるということを表しています。

直感的には、命題(3)が成り立つことから定義域の各元に対して値域の元をひとつ定めている、つまり $f_{2}$ が写像である(定義がwell-definedである)と言えます（数学の本や講義資料ではよく、「 $f_{2}$ の定義がwell-definedであることをいうためには命題(3)を示せば良い」という言い方をします）。ただし、本当にそう言えるということを厳密に示そうとすると、少し曖昧な部分があってモヤっとします。

「命題(3)が成り立つ

⟹

f_{2}

の定義がwell-defined」の証明

命題(3)が成り立つ

⟹

f_{2}

の定義がwell-defined

定義域 $Z / \sim \times Z / \sim$ の各元に対して値域 $Z / \sim$ の元を1つ定めていることを示せばよいです。定義域の各元に対して値域の元を1つ以上定めていることは明らかです。そこで、定義域の各元に対して、値域の元が対応していれば一意であること、つまり任意の $x \in Z / \sim \times Z / \sim$ 、任意の $y_{1}, y_{2} \in Z / \sim$ に対して、 $x \mapsto y_{1}$ ( $f_{2}$ の定義による $x$ から $y_{1}$ への対応)と $x \mapsto y_{2}$ ( $f_{2}$ の定義による $x$ から $y_{2}$ への対応)があるならば、 $y_{1} = y_{2}$ であることを示せば良いです。

任意の $x \in Z / \sim \times Z / \sim$ 、任意の $y_{1}, y_{2} \in Z / \sim$ に対して、 $x \mapsto y_{1}$ と $x \mapsto y_{2}$ の対応があるとします。
$f_{2}$ の定義と $x \mapsto y_{1}$ から、ある $a_{1}, b_{1} \in Z$ が存在して、 $x = ([a_{1}], [b_{1}]), y_{1} = [a_{1} + b_{1}]$ が成り立ちます。
同様に、 $f_{2}$ の定義と $x \mapsto y_{2}$ から、ある $a_{2}, b_{2} \in Z$ が存在して、 $x = ([a_{2}], [b_{1}]), y_{2} = [a_{2} + b_{2}]$ が成り立ちます。
命題(3)と $x = ([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ から、 $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ 、つまり $y_{1} = y_{2}$ が成り立ちます。

以上から、定義域の各元に対して値域の元を1つ定めている、つまり

f_{2}

の定義がwell-definedであることが言えます。

モヤッとなる原因として次の２つが挙げられます。

写像の定義（定義域の各元に対して、値域の元をひとつ定める対応）が少し曖昧なこと（対応とはなにか）
$f_{2}$ が写像かどうかまだわからない段階では、 $f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ という定義は何を定義しているのかが謎。何を定義しているのか謎だが証明に使うことになる。

そこでこの記事では、写像とはなにかを厳密に定義します。具体的には、写像を二項関係の特殊なものとして定義します。
また、 $f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ という定義は、 $f_{2}$ が写像かどうかわからない段階では ${(([a], [b]), [a + b]) ∣ a, b \in Z}$ で定まる $Z / \sim \times Z / \sim$ と $Z / \sim$ の間の二項関係を定義していると解釈します。この二項関係が写像の条件を満たすかどうかということを考えることで、 $f_{2}$ の定義が写像の定義としてwell-definedであるかを考えます。

写像は二項関係の特殊なもの

写像は二項関係の特殊なものとして定義できることを紹介します。まずは二項関係を定義します。

二項関係

$X, Y$ を集合とします。 $G \subseteq X \times Y$ とします。このとき、3つ組 $R = ⟨ X, Y, G ⟩$ を $X$ と $Y$ との間の二項関係といいます。 $G$ を二項関係 $R$ のグラフといいます。

一般には $G$ 自体を二項関係と呼ぶことが多いですが、この記事では写像の一般化として二項関係を用いるため、 $X, Y$ を含めた3つ組として二項関係を定義します。
次に二項関係を用いて写像を定義します。

写像

$f = ⟨ X, Y, G ⟩$ を二項関係とします。二項関係 $f$ が次の性質を満たしているとします。

左全域性: 任意の $x \in X$ に対して、ある $y \in Y$ が存在して、 $(x, y) \in G$
右一意性: 任意の $x \in X$ と任意の $y_{1}, y_{2} \in Y$ に対して、 $(x, y_{1}), (x, y_{2}) \in G$ ならば $y_{1} = y_{2}$

このとき、二項関係 $f$ を $X$ から $Y$ への写像といいます。二項関係 $f$ が $X$ から $Y$ への写像であることを $f : X \to Y$ と書きます。

$x \in X$ を任意に取ります。左全域性と右一意性から、「ある $y \in Y$ が一意に存在して、 $(x, y) \in G$ 」が成り立ちます。そのような $y$ を $f (x)$ と表記します。つまり、任意の $x \in X, y \in Y$ に対して $(x, y) \in G ⟺ y = f (x)$ が成り立ちます。

$G$ を写像 $f$ のグラフといいます。また、 $G = {(x, f (x)) ∣ x \in X}$ が成り立ちます。

左全域性は「任意の $x \in X$ に対して、 $x$ に対応する $Y$ の元が少なくても一つは存在する」ことを言っていて、右一意性は「任意の $x \in X$ に対して、 $x$ に対応する $Y$ の元は存在すれば一意である」ことを言っています。

写像の例

$X = {0, 1, 2}$ , $Y = {3, 4, 5}$ とし、 $G = {(0, 3), (1, 4), (2, 3)}$ とします。このとき、二項関係 $f = ⟨ X, Y, G ⟩$ は写像です。 $f (0) = 3$ , $f (1) = 4$ , $f (2) = 3$ を満たします。

写像でない例（左全域性を満たさない）

$X = {0, 1, 2}$ , $Y = {3, 4, 5}$ とし、 $G = {(0, 3), (1, 4)}$ とします。このとき、二項関係 $f = ⟨ X, Y, G ⟩$ は左全域性を満たさないので、写像ではありません。（ $(2, y) \in G$ となる $y \in Y$ が存在しないため、左全域性を満たしていないです。）

写像でない例（右一意性を満たさない）

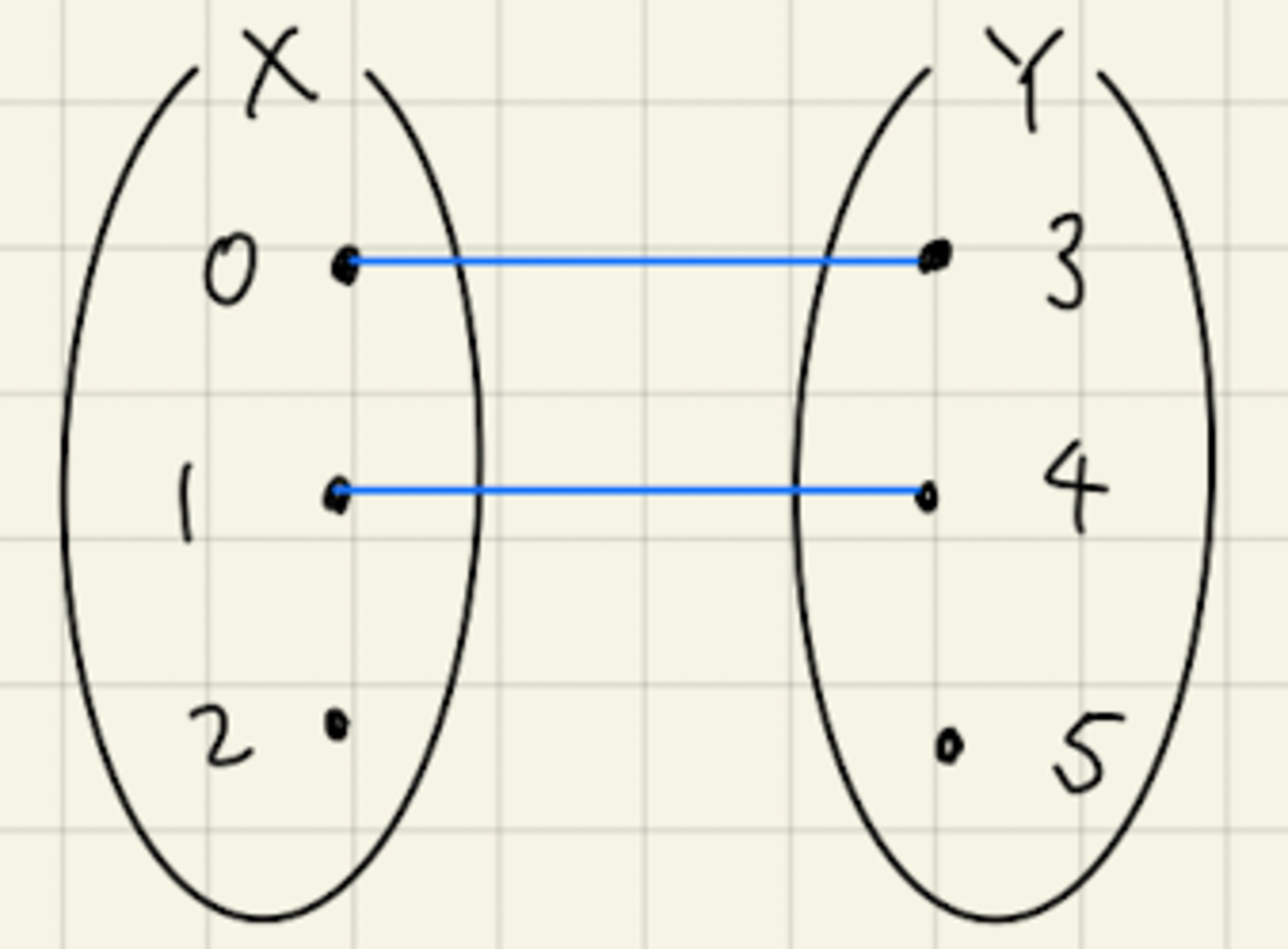
$X = {0, 1, 2}$ , $Y = {3, 4, 5}$ とし、 $G = {(0, 3), (0, 5), (1, 3), (2, 4)}$ とします。このとき、二項関係 $f = ⟨ X, Y, G ⟩$ は右一意性を満たさないので、写像ではありません。（ $(0, 3), (0, 5) \in G$ ですが、 $3 \neq 5$ です。入力 $0$ に対して、 $3, 5$ の2つの出力が対応してしまっています。つまり右一意性を満たしていません。）

写像を定義する表記

一般に写像を定義するとき、 $f : Z \to Z; n \mapsto n + 1$ のように書くことがあります。この記事の定式化では $f = ⟨ Z, Z, G ⟩$ （ただし、 $G = {(n, n + 1) ∣ n \in Z}$ ）と書けます。

本題

「well-definedとは」の章では、次の2つの写像の定義を例に上げました。

$f_{1} : Z / \sim \to Z / \sim; [a] \mapsto [| a |] (a \in Z)$
$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$

$f_{1}$ の例はwell-definedでない例として紹介し、 $f_{2}$ はwell-definedの例として紹介しました。
「写像は二項関係の特別なもの」という考え方を用いると、写像の定義がwell-definedであるとは、「その写像の定義を二項関係としてみたときに、その二項関係が写像である」という解釈を与えることができます。
ここでは、 $f_{1}, f_{2}$ の定義を二項関係の定義としてみて、その二項関係が写像であるかどうかを見てwell-definedかどうかを見ていきます。

$f_{1} : Z / \sim \to Z / \sim; [a] \mapsto [| a |] (a \in Z)$ の場合、
$f_{1} = ⟨ Z / \sim, Z / \sim, G_{1} ⟩$ (ただし、 $G_{1} = {([a], [| a |]) ∣ a \in Z}$ )という二項関係を定義しているという解釈ができます。 $f_{1}$ を二項関係として見たとき、二項関係 $f_{1}$ は右一意性（任意の $x \in Z / \sim$ 、任意の $y_{1}, y_{2} \in Z / \sim$ に対して $(x, y_{1}), (x, y_{2}) \in G_{1}$ ならば $y_{1} = y_{2}$ ）を満たしません( $x = [1] = [- 2], y_{1} = [1], y_{2} = [2]$ )。よって、二項関係 $f_{1}$ は写像でないです（なお、左全域性は満たします）。こういうときは $f_{1}$ の定義はwell-definedでないと言えます。

$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ の場合は、
$f_{2} = ⟨ Z / \sim \times Z / \sim, Z / \sim, G_{2} ⟩$ (ただし、 $G_{2} = {(([a], [b]), [a + b]) ∣ a, b \in Z}$ )という二項関係を定義しているという解釈ができます。 $f_{2}$ を二項関係としてみたとき、後で見るように二項関係 $f_{2}$ は左全域性と右一意性を満たします。よって、二項関係 $f_{2}$ は写像です。こういう場合には $f_{2}$ の定義はwell-definedであると言えます。

次に、二項関係 $f_{2}$ が左全域性と右一意性が成り立つことを確認します。左全域性を満たすことは明らかです。一応証明を書くと次のようになります。

二項関係

f_{2}

の左全域性

左全域性の定義から「任意の $x \in Z / \sim \times Z / \sim$ に対して、ある $y \in Z / \sim$ が存在して、 $(x, y) \in G_{2}$ 」であることを示せばよいです。

$x \in Z / \sim \times Z / \sim$ を任意にとります。 $Z / \sim$ の定義から、ある $a, b \in Z$ が存在して、 $x = ([a], [b])$ が成り立ちます。
$y = [a + b]$ とすると、 $(x, y) \in G_{2}$ が成り立ちます。

以上から、二項関係 $f_{2}$ は左全域性を満たします。

次に右一意性を満たすことを証明します。この証明には「well-definedとは」の章で出てきた命題(3)
(3) 「任意の $a_{1}, b_{1}, a_{2}, b_{2} \in Z$ に対して、 $([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ ならば $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ 」
が成り立つことを用います。

二項関係

f_{2}

の右一意性

右一意性の定義から「任意の $x \in Z / \sim \times Z / \sim$ と任意の $y_{1}, y_{2} \in Z / \sim$ に対して、 $(x, y_{1}), (x, y_{2}) \in G_{2}$ ならば $y_{1} = y_{2}$ 」であることを示せばよいです。

$x \in Z / \sim \times Z / \sim$ と $y_{1}, y_{2} \in Z / \sim$ を任意にとって固定し、 $(x, y_{1}), (x, y_{2}) \in G_{2}$ が成り立つと仮定します。
$(x, y_{1}) \in G_{2}$ から、ある $a_{1}, b_{1} \in Z$ が存在して、 $(x, y_{1}) = (([a_{1}], [b_{1}]), [a_{1} + b_{1}])$ が成り立ちます。
$(x, y_{2}) \in G_{2}$ から、ある $a_{2}, b_{2} \in Z$ が存在して、 $(x, y_{2}) = (([a_{2}], [b_{2}]), [a_{2} + b_{2}])$ が成り立ちます。
$x = ([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ と命題(3)から $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ が成り立ちます。
つまり、 $y_{1} = y_{2}$ が成り立ちます。

以上から、二項関係 $f_{2}$ は右一意性を満たします。

命題(3)が右一意性を示すのに重要な命題になっていて、命題(3)が示せたら右一意性が言える、と表現することができます。左全域性はほとんど自明なので、命題(3)が示せたらwell-definedであることが言える、と表現することもできます。

実は、右一意性を認めたら命題(3)を導出することができます（後で一般化して示します）。つまり命題(3)と右一意性は同値で、命題(3)は右一意性を表していると解釈することもできます。

一般化

今までの話を一般化して考えていきます。

$f_{1}, f_{2}$ の写像の定義

$f_{1} : Z / \sim \to Z / \sim; [a] \mapsto [| a |] (a \in Z)$
$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$

のwell-defined性の話は次のように一般化できます。

写像のwell-defined性

$X, X^{'}, Y$ を集合とし、 $p : X \to X^{'}, f : X \to Y$ を写像とします。
$\tilde{f} : X^{'} \to Y; p (x) \mapsto f (x) (x \in X)$ が写像の定義としてwell-definedであることを次のように定義します。

$\tilde{f}$ を二項関係として $\tilde{f} = ⟨ X^{'}, Y, G ⟩$ （ただし $G = {(p (x), f (x)) ∣ x \in X}$ ）と定義したとき、二項関係 $\tilde{f}$ が写像である（つまり二項関係 $\tilde{f}$ が左全域性と右一意性を満たす）。

$\tilde{f}$ の定義がwell-definedである場合、3つの写像 $p, f, \tilde{f}$ には次の関係があります（つまり $f = \tilde{f} \circ p$ が成り立ちます）。

$X f p Y X^{'} \tilde{f}$

f_{1}

での例

$f_{1} : Z / \sim \to Z / \sim; [a] \mapsto [| a |] (a \in Z)$ について

$\tilde{f} : X^{'} \to Y; p (x) \mapsto f (x) (x \in X)$
の $X, X^{'}, Y, p, f$ を次のように設定すると、 $f_{1} = \tilde{f}$ になります。

$X = Z$
$X^{'} = Z / \sim$
$Y = Z / \sim$
$p : Z \to Z / \sim; a \mapsto [a]$
$f : Z \to Z / \sim; a \mapsto [| a |]$

先程見たとおり、 $f_{1}$ を二項関係としてみたとき右一意性を満たさないので写像ではない、つまりwell-definedではないです。

f_{2}

での例

$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ について

$\tilde{f} : X^{'} \to Y; p (x) \mapsto f (x) (x \in X)$
の $X, X^{'}, Y, p, f$ を次のように設定すると、 $f_{2} = \tilde{f}$ になります。

$X = Z \times Z$
$X^{'} = Z / \sim \times Z / \sim$
$Y = Z / \sim$
$p : Z \times Z \to Z / \sim \times Z / \sim; (a, b) \mapsto ([a], [b])$
$f : Z \times Z \to Z / \sim; (a, b) \mapsto [a + b]$

$p, f, \tilde{f} (= f_{2})$ の関係を図に表すと次のようになります。

先程見たとおり、 $f_{2}$ を二項関係としてみたとき左全域性と右一意性を満たすので写像で、つまりwell-definedです。

$\tilde{f} : X^{'} \to Y; p (x) \mapsto f (x) (x \in X)$ の形で定義される写像のwell-defined性の確認（つまり左全域性と右一意性の確認）には次の定理が使えます。

$X, X^{'}, Y$ を集合とし、 $p : X \to X^{'}, f : X \to Y$ を写像とします。 $\tilde{f} : X^{'} \to Y; p (x) \mapsto f (x) (x \in X)$ が写像の定義としてwell-definedかどうかについて考えます。 $\tilde{f}$ を二項関係として $\tilde{f} = ⟨ X^{'}, Y, G ⟩$ （ただし $G = {(p (x), f (x)) ∣ x \in X}$ ）と定義したとき、次の命題が成り立ちます。

二項関係 $\tilde{f}$ が左全域性を満たす $⟺$ 写像 $p$ が全射
二項関係 $\tilde{f}$ が右一意性を満たす $⟺$ 任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$

証明は後に載せます。この定理は $\tilde{f} : X^{'} \to Y; p (x) \mapsto f (x) (x \in X)$ の定義がwell-definedであることを示すためには次の2つを示せば良いということを言っています。

写像 $p$ が全射であること
任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$ が成り立つこと

多くの場合 $p$ が全射なのは自明で、2つめを示せばwell-definedであることが言えます。
以下、定理を用いた例を提示します。

f_{1}

の例

$f_{1} : Z / \sim \to Z / \sim; [a] \mapsto [| a |] (a \in Z)$ について
（ $p : Z \to Z / \sim; a \mapsto [a]$ , $f : Z \to Z / \sim; a \mapsto [| a |]$ ）

$p$ は全射です（ $f_{1}$ の定義によらず、商集合の性質から言えます）。つまり、 $f_{1}$ は左全域性を満たします。

一方、「任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$ 」すなわち「任意の $a_{1}, a_{2} \in Z$ に対して $[a_{1}] = [a_{2}]$ ならば $[| a_{1} |] = [| a_{2} |]$ 」は成り立ちません（ $a_{1} = 1, a_{2} = - 2$ ）。よって $f_{1}$ は右一意性を満たしません。

f_{2}

の例

$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ について
（ $p : Z \times Z \to Z / \sim \times Z / \sim; (a, b) \mapsto ([a], [b])$ , $f : Z \times Z \to Z / \sim; (a, b) \mapsto [a + b]$ ）

$p$ は全射です（ $f_{2}$ の定義によらず、商集合の性質から言えます）。つまり、 $f_{2}$ は左全域性を満たします。

「任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$ 」すなわち「任意の $(a_{1}, b_{1}), (a_{2}, b_{2}) \in Z \times Z$ に対して $([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ ならば $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ 」(これは命題(3)と同じことをいっています)は成り立ちます。よって、 $f_{2}$ は右一意性を満たします。

以上から、 $f_{2}$ の定義は写像の定義としてwell-definedと言えます。

この定理からも分かる通り、命題(3)は右一意性と同値な命題になっていて、命題(3)は右一意性を表しているという解釈ができます。

最後に定理1の証明を与えておきます。

二項関係

\tilde{f}

が左全域性を満たす

⟹

写像

p

が全射

$\tilde{f}$ が左全域性を満たすと仮定します。
$p$ が全射、つまり「任意の $x^{'} \in X$ に対してある $x \in X$ が存在して $x^{'} = p (x)$ が成り立つ」ことを示します。

$x^{'} \in X^{'}$ を任意に取って固定します。 $\tilde{f}$ の左全域性から、ある $y \in Y$ が存在して $(x^{'}, y) \in G$ が成り立ちます。 $G$ の定義からある $x \in X$ が存在して、 $(x^{'}, y) = (p (x), f (x))$ が成り立ち、とくに $x^{'} = p (x)$ が成り立ちます。

以上から $p$ は全射です。

二項関係

\tilde{f}

が左全域性を満たす

⟸

写像

p

が全射

$p$ が全射であると仮定します。
$\tilde{f}$ が左全域性を満たす、つまり「任意の $x^{'} \in X^{'}$ に対してある $y \in Y$ が存在して $(x^{'}, y) \in G$ が成り立つ」ことを証明します。

$x^{'} \in X^{'}$ を任意に取って固定します。 $p$ が全射であることから、ある $x \in X$ が存在して、 $x^{'} = p (x)$ が成り立ちます。ここで $y = f (x)$ とすると、 $y \in Y$ で、 $(x^{'}, y) = (p (x), f (x)) \in G$ が成り立ちます。

よって、 $\tilde{f}$ は左全域性を満たします。

二項関係

\tilde{f}

が右一意性を満たす

⟹

任意の

x_{1}, x_{2} \in X

に対して

p (x_{1}) = p (x_{2})

ならば

f (x_{1}) = f (x_{2})

$\tilde{f}$ が右一意性（任意の $x^{'} \in X$ , $y_{1}, y_{2} \in Y$ に対して $(x^{'}, y_{1}), (x^{'}, y_{2}) \in G$ ならば $y_{1} = y_{2}$ ）を満たすと仮定します。
「任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$ 」が成り立つことを示します。

$x_{1}, x_{2} \in X$ を任意にとって固定し、 $p (x_{1}) = p (x_{2})$ が成り立つと仮定します。 $G$ の定義から $(p (x_{1}), f (x_{1})), (p (x_{2}), f (x_{2})) \in G$ が成り立ちます。
$\tilde{f}$ の右一意性と $p (x_{1}) = p (x_{2})$ と $(p (x_{1}), f (x_{1})), (p (x_{2}), f (x_{2})) \in G$ から $f (x_{1}) = f (x_{2})$ が成り立ちます。

よって、「任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$ 」が成り立ちます。

二項関係

\tilde{f}

が右一意性を満たす

⟸

任意の

x_{1}, x_{2} \in X

に対して

p (x_{1}) = p (x_{2})

ならば

f (x_{1}) = f (x_{2})

「任意の $x_{1}, x_{2} \in X$ に対して $p (x_{1}) = p (x_{2})$ ならば $f (x_{1}) = f (x_{2})$ 」（☆）が成り立つと仮定します。
$\tilde{f}$ が右一意性を満たす、つまり「任意の $x^{'} \in X$ , $y_{1}, y_{2} \in Y$ に対して $(x^{'}, y_{1}), (x^{'}, y_{2}) \in G$ ならば $y_{1} = y_{2}$ を満たす」ことを示します。

$x^{'} \in X^{'}, y_{1}, y_{2} \in Y$ を任意にとって固定し、 $(x^{'}, y_{1}), (x^{'}, y_{2}) \in G$ が成り立つと仮定します。
$(x^{'}, y_{1}) \in G$ から、ある $x_{1} \in X$ が存在して、 $(x^{'}, y_{1}) = (p (x_{1}), f (x_{1}))$ が成り立ちます。
$(x^{'}, y_{2}) \in G$ から、ある $x_{2} \in X$ が存在して、 $(x^{'}, y_{2}) = (p (x_{2}), f (x_{2}))$ が成り立ちます。
仮定の（☆）と $x^{'} = p (x_{1}) = p (x_{2})$ から $f (x_{1}) = f (x_{2})$ が成り立ちます。つまり、 $y_{1} = y_{2}$ が成り立ちます。

よって、 $\tilde{f}$ は右一意性を満たします。

おわりに

写像であると期待して定義したものが写像かどうかまだわからない段階では、その定義をある二項関係の定義として見て、その二項関係が写像である（左全域性と右一意性を満たしている）ときに写像の定義としてwell-definedである、という解釈を与えました。

写像の定義がwell-definedであることをいうときに示す命題、例えば
$f_{2} : Z / \sim \times Z / \sim \to Z / \sim; ([a], [b]) \mapsto [a + b] (a, b \in Z)$ がwell-definedであることをいうときに示す命題
(3) 「任意の $a_{1}, b_{1}, a_{2}, b_{2} \in Z$ に対して、 $([a_{1}], [b_{1}]) = ([a_{2}], [b_{2}])$ ならば $[a_{1} + b_{1}] = [a_{2} + b_{2}]$ 」
は二項関係の右一意性という解釈ができて、確かに命題(3)が言えればwell-definedであることがすぐに言えることを確認しました。