図形と複素数２

解答

$|z|=1$である。$\displaystyle{z=\frac{w-i}2}$として，代入し，

$$\left|\frac{w-i}2\right|=1$$

$$\frac{|w-i|}{2}=1$$

$$|w-i|=2$$

よって，点$w$は点$i$を中心，半径$2$の円を描く。

図形的な説明（変換）

• 点$w$は点$z$をどのように動かした（変換した）のか考えてみる。$w=2z+i$なので，点$z$を原点を中心に2倍に拡大して，その後，$i$だけ，平行移動すると，点$w$となる。

• また，$w=2z+i$は

$$w+i=2(z+i)$$

と変形できるので，『点$z$を点$-i$を中心に2倍に拡大すると，点$w$となる。』とも説明できる。この$-i$は不動点を求める計算は次のようになる。数列の漸化式の特性方程式と類似性がある。

$$\alpha=2\alpha+i\quad \therefore \alpha=-i$$

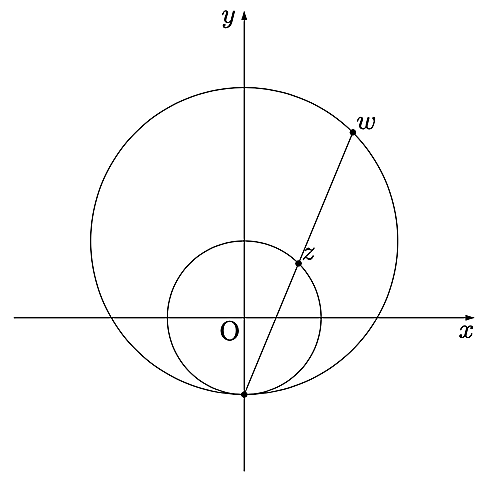変換の様子