ロピタルの定理のWikipedia記事を見て考えたこと
はじめに
この記事はロピタルの定理のWikipedia記事( 日本語版 ・ 英語版 )を見て気になったところを書いたものです。
まずはロピタルの定理をおさらいしましょう。
$I$は$c\in[-\infty,+\infty]$を含む開区間($c=\pm\infty$なら、$I$は十分大きい(小さい)実数の集合)で、
$f,g:I\rightarrow\mathbb{R}$は微分可能関数で、次の(1),(2)のどちらかの条件を満たすものとする。
(1) $\displaystyle\lim_{x\rightarrow c}f(x)=0$かつ$\displaystyle\lim_{x\rightarrow c}g(x)=0$
(2) $\displaystyle\lim_{x\rightarrow c}f(x)=\pm\infty$かつ$\displaystyle\lim_{x\rightarrow c}g(x)=\pm\infty$
また、任意の$x\in I-\{c\}$において、$g'(x)\ne0$であるとする。
ここで、$\displaystyle\lim_{x\rightarrow c}\frac{f'(x)}{g'(x)}=L\in[-\infty,+\infty]$となる$L$が存在すれば、$\displaystyle\lim_{x\rightarrow c}\frac{f(x)}{g(x)}=L$である。
日本語版ロピタルの定理の記事にあったあやしい記述
2021/03/29時点で、日本語版Wikipedia記事に以下の記述があります。
問題の箇所
誤字修正&ところどころ改行したものがこちら↓
ロピタルの定理はしばしば巧妙な方法において引き合いに出される。
ここで$\displaystyle f(x)+f'(x)$が$\displaystyle x\to\infty$で収束すると、
\begin{align}
\lim_{x\to\infty}f(x) & = \lim_{x\to\infty}{e^{x}f(x)\over e^{x}} & \cdots(1)\\
& = \lim_{x\to\infty}{e^{x}(f(x)+f'(x))\over e^{x}} & \cdots(2)\\
& = \lim_{x\to\infty}(f(x)+f'(x)) & \cdots(3)
\end{align}
であるので極限$\displaystyle\lim_{x\to\infty}f(x)$が存在し、$\displaystyle\lim_{x\to\infty}f'(x)=0$である。
つまり、敢えて分母・分子に$e^x$を掛けて(1)、
$\frac{\infty}{\infty}$の不定形にした上でロピタルの定理を適用し(2)、
再び分母・分子の$e^x$を約分しています(3)。
なかなか技巧的・・・。
しかし、よく考えてみると、$e^xf(x)$が$\infty$に発散するとは限りません。
例えば$f(x)=e^{-x}$だと$e^xf(x)=1$になってしまい、ロピタルの定理が使えないです。
この論証は、$\displaystyle\lim_{x\to\infty}e^xf(x)=\pm\infty$のときに限った話になりそうです。
$f:\mathbb{R}\rightarrow\mathbb{R}$は微分可能関数で、$\displaystyle\lim_{x\to\infty}\displaystyle f(x)+f'(x)$が収束し、$\displaystyle\lim_{x\to\infty}e^xf(x)=\pm\infty$であるとする。
このとき、極限$\displaystyle\lim_{x\to\infty}f(x)$が存在し、$\displaystyle\lim_{x\to\infty}f'(x)=0$である。
ここで気になった疑問
もし、$\displaystyle\lim_{x\to\infty}e^xf(x)\ne\pm\infty$だった場合にはロピタルの定理は使えないのは前述の通りですが、結論の「$f(x)$の極限の存在」や「$f'(x)\to0$」は本当なのでしょうか？
$f:\mathbb{R}\rightarrow\mathbb{R}$は微分可能関数で、$\displaystyle\lim_{x\to\infty}\displaystyle f(x)+f'(x)$が収束するとする。
このとき、極限$\displaystyle\lim_{x\to\infty}f(x)$が存在し、$\displaystyle\lim_{x\to\infty}f'(x)=0$になるという主張は真だろうか？
偽だとしたら反例はどのようなものだろうか？
これが偽だと思って反例しばらく探しても全然見つからないんです・・・
例えば、$\displaystyle\lim_{x\to\infty}e^xf(x)$が$M$に収束するとしましょう。
すると、
\begin{align}
\lim_{x\to\infty}f(x) & = \lim_{x\to\infty}e^{x}f(x)\times e^{-x}\\
& = M\times0\\
& = 0
\end{align}
となります。
さらに仮定より$\displaystyle\lim_{x\to\infty}f'(x)$が収束することが分かります。その極限値を$L$とします。
もし$L\ne0$だったら、十分大きい実数$x$に対し、$f(x)$は傾き$L$の$1$次関数に近い挙動を示すことになり、従って$\displaystyle\lim_{x\to\infty}f(x)$は発散するので矛盾しています。(厳密には$\varepsilon-\delta$論法を使うことになると思います)
以上のことから、$\displaystyle\lim_{x\to\infty}f'(x)=0$となります。
よって、$\displaystyle\lim_{x\to\infty}e^xf(x)=\pm\infty$の場合と同様、$\displaystyle\lim_{x\to\infty}e^xf(x)$が収束する場合でも同じ結論に至ることがわかりました。
しかし、$e^xf(x)$が振動する場合がまだ残っています。振動するといっても、有界の範囲で振動するパターンもあれば、非有界のパターンもあります。非有界のパターンも、上限か下限の一方はあってもう一方がない場合もあるし、上にも下にも非有界の場合もあります。そう考えていくと、いろいろ細かく場合分けして別々に証明・反証を考えるのはなかなか面倒な気がしますね。
英語版Wikipediaの記載
日本語版Wikipedia記事は、昔(2009年頃)の英語版の和訳をそのまま書いているだけで、現在の英語版には注意書きがあります。
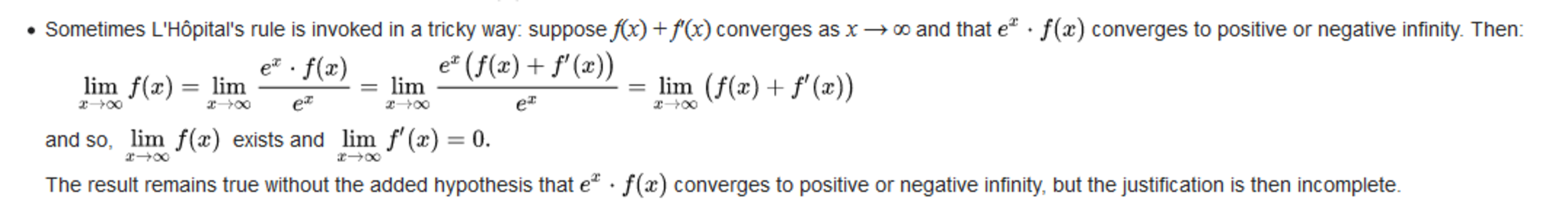現在の英語版Wikipediaの記載
Sometimes L'Hôpital's rule is invoked in a tricky way: suppose f(x) + f′(x) converges as x → ∞ and that $\displaystyle e^{x}\cdot f(x)$ converges to positive or negative infinity. Then:
$\displaystyle \lim _{x\to \infty }f(x)=\lim _{x\to \infty }{\frac {e^{x}\cdot f(x)}{e^{x}}}=\lim _{x\to \infty }{\frac {e^{x}{\bigl (}f(x)+f'(x){\bigr )}}{e^{x}}}=\lim _{x\to \infty }{\bigl (}f(x)+f'(x){\bigr )}$
and so, $\displaystyle \lim _{x\to \infty }f(x)$ exists and $\displaystyle \lim _{x\to \infty }f'(x)=0.$
The result remains true without the added hypothesis that $\displaystyle e^{x}\cdot f(x)$ converges to positive or negative infinity, but the justification is then incomplete.
ざっとこんなこと言ってる↓
ロピタルの定理はしばしばトリッキーな方法で使われる。
ここで、$f(x)+f'(x)$が$x\to\infty$で収束し、$e^{x}\cdot f(x)$が正または負の無限大に発散するとする。
このとき、
$\displaystyle \lim_{x\to\infty}f(x)=\lim_{x\to\infty}{\frac{e^{x}\cdot f(x)}{e^{x}}}=\lim_{x\to\infty}{\frac{e^{x}{\bigl(}f(x)+f'(x){\bigr)}}{e^{x}}}=\lim_{x\to\infty}{\bigl(}f(x)+f'(x){\bigr)}$
であるから、$\displaystyle\lim_{x\to\infty}f(x)$が存在し$\displaystyle \lim_{x\to\infty}f'(x)=0$である。
$e^{x}\cdot f(x)$が正または負の無限大に収束するという仮定がなくても結論は正しいままだが、(このままでは)不完全だから正当化できない。
厳密な証明は書かれてないものの、$\displaystyle\lim_{x\to\infty}e^xf(x)$の極限にかかわらず、主張は正しいようです。
あやしい主張を証明してみる
$\displaystyle\lim_{x\to\infty}e^xf(x)$の振る舞いによって細かくパターン分けせずに、統一した証明を考えます。($\varepsilon-\delta$論法を使います)
$f:\mathbb{R}\rightarrow\mathbb{R}$は微分可能関数で、$\displaystyle\lim_{x\to\infty}\displaystyle f(x)+f'(x)$が収束するとする。
このとき、極限$\displaystyle\lim_{x\to\infty}f(x)$が存在し、$\displaystyle\lim_{x\to\infty}f'(x)=0$である。
$\displaystyle\lim_{x\to\infty}\displaystyle f(x)+f'(x)$の極限値を$a$とします。
目標は$\displaystyle\lim_{x\to\infty}\displaystyle f(x)=a$を証明することで、これにより$\displaystyle\lim_{x\to\infty}\displaystyle f'(x)=0$は自動的にわかります。
$\displaystyle\lim_{x\to\infty}\displaystyle f(x)+f'(x)=a$は、
どんな$\varepsilon>0$に対しても、命題「$x>R\Rightarrow -\varepsilon< f(x)+f'(x)-a<\varepsilon$」が真となるような実数$R$があるということです。
ここで、$t\in(R,x)$に対し、関数$e^{t-R}(f(t)-a)$を考えます。
$t$で微分した式は、
$\displaystyle \frac{d}{dt}e^{t-R}(f(t)-a)=e^{t-R}(f(t)+f'(t)-a)<\varepsilon e^{t-R}$
と評価できます。
さらに、$t$を$R$から$x$の範囲で積分すると、
$e^{x-R}(f(x)-a)-(f(R)-a)<\varepsilon(e^{x-R}-1)$
右辺の分かりやすさのために、評価を甘くして
$e^{x-R}(f(x)-a)-(f(R)-a)<\varepsilon e^{x-R}$
としましょう。式を変形して、
$f(x)-a<(f(R)-a)e^{-(x-R)}+\varepsilon$
$x$を大きくすると、右辺の$(f(R)-a)e^{-(x-R)}$は$0$に近づきます。
具体的には$x>\max\{R,R-\log\frac{\varepsilon}{|f(R)-a|}\}$となるように$x$を再定義してあげれば、
$(f(R)-a)e^{-(x-R)}<\varepsilon$になりますので、
$f(x)-a<(f(R)-a)e^{-(x-R)}+\varepsilon<\varepsilon+\varepsilon=2\varepsilon$
と上から評価できました。
同様に$-\varepsilon< f(x)+f'(x)-a$は$-f(x)-f'(x)+a<\varepsilon$なので、
関数$-e^{t-R}(f(t)-a)$を考えれば、上記と同じように、
$-f(x)+a<2\varepsilon$
すなわち
$-2\varepsilon< f(x)-a$
と下から評価ができます。
したがって、任意の$\varepsilon>0$に対して、十分大きい$x$について$-2\varepsilon< f(x)-a<2\varepsilon$となり、
$\displaystyle\lim_{x\to\infty}\displaystyle f(x)=a$が証明できました。
これでロピタルの定理では説明ができないあやしい部分も補うことができました。
個人的に満足です。
以上、読んでいただきありがとうございました。