小学生でもπ>3.05を証明したい！

はじめに

このサイトを利用するほど数学が好きな皆さんなら恐らく99%の方がご存じかとは思いますが、東京大学の入試問題でかつてこのような問題が出されたことがありました。

この問題文の圧倒的な短さ、小学生でもわかる簡潔さなどから18年経った今でも有名なこちらの問題、その話題性から数多くのサイト、YouTube上に解説動画が上げられました。ある解説では余弦定理を用いて、ある解説では積分を用いて、またある解説では三平方の定理までの定理、公式を用いた解法など、様々な解き方が考えられてきました。

今回はこの問題を初等教育の範囲だけで解いていきたいと思います。

レギュレーション

今回のレギュレーションは 文部科学省のホームページ に従います。

これを見るのが面倒だよって人向けの簡易的なリストも置いておきます。

できる・使えることの一例

• 円周率の定義
• 円周の公式、円の面積の公式
• 四則演算
• 相似、合同
• 等積変形
• 反例を示すことによる否定
• 不等式

(おもに)以上のことが使用可能です。

できない・使えないことの一例

• 平方根
• 三平方の定理
• 三角関数
• 球の体積、表面積
• 因数分解

(おもに)以上のことは使用不可能です。

証明

半径2の円に内接する正十角形を考える。
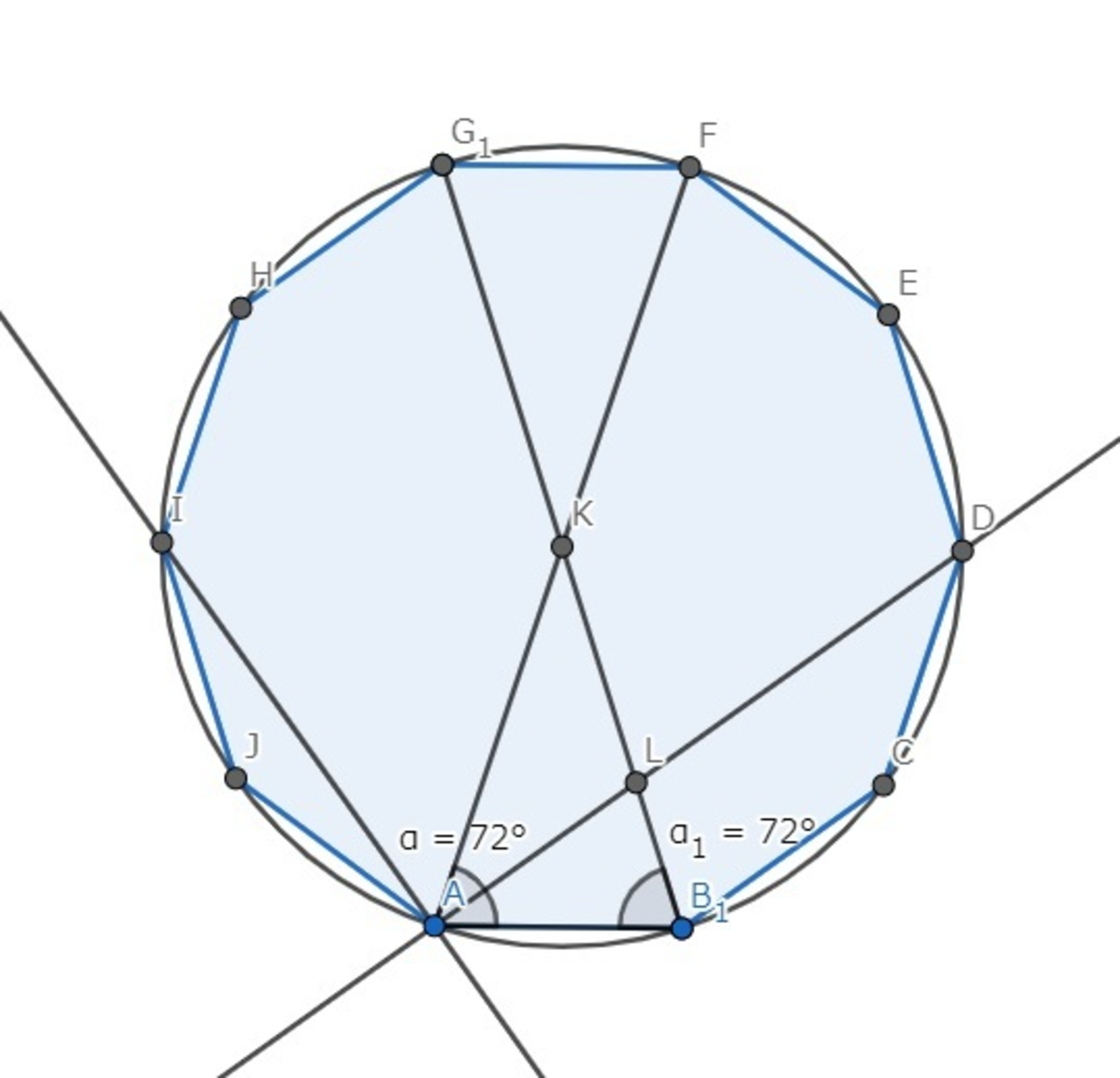(GeoGebraの使い方が雑なのは許してください)

A～Jは円を10等分しているため∠AKB=36°であり、△KABは∠KAB=∠KBA=72°の二等辺三角形である。∠KABの角の二等分線を引き、線分KBとの交点をLとすると、∠LAB=36°、∠ALB=180-(36+72)=72°より△ALBはAL=ABの二等辺三角形である。また、∠LAK=36°より△ALKはAL=KLの二等辺三角形である。

AB=〇、LB=△とおくと

AB=KL、KL+LB=KBより　〇+△=2　……①

また、∠LAB=∠AKB、∠ALB=∠KABより△KABと△ALKは相似である。相似の比の関係より、AB:BL=KA:AB
比の性質よりAB×AB=BL×KAが言えるので　〇×〇=2×△　……②

以上の二式が導出できる。

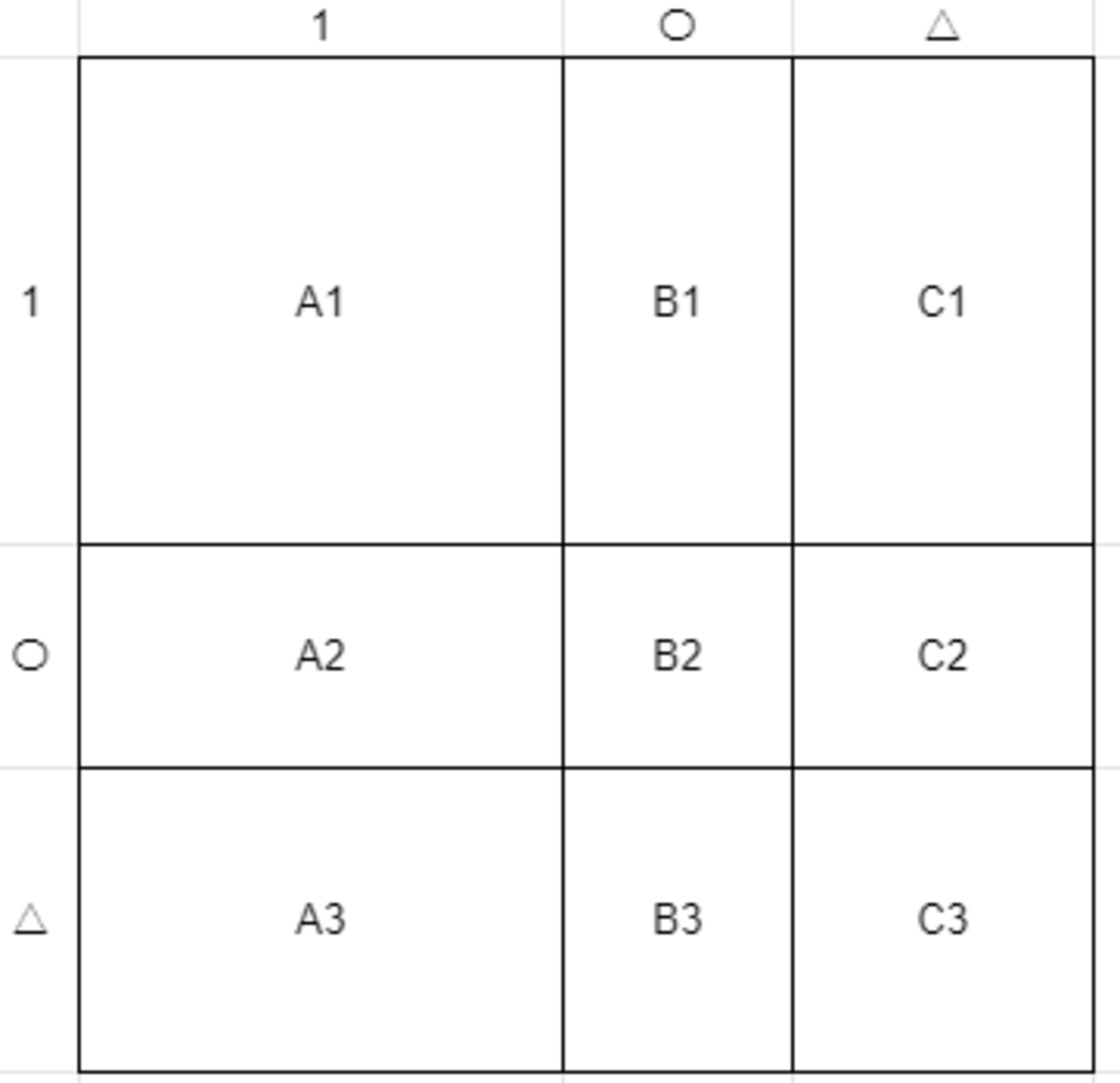(Excelで作成した画像なので長さは厳密ではありません)

①より、B2+B3の面積は〇×2である。したがって、C3の面積はA2+B1の面積に等しい。また、②よりC2+C3の面積はB2に等しい。①よりB2+B3+C2+C3の面積は4であるから、A1+A2+B1+B2=B2+B3+C2+C3+1=5となる。

2.23×2.23=4.9729より、〇>1.23である。

従って、正十角形の辺の長さの合計は1.23×10=12.3以上である。一方、正十角形に外接する円弧の長さは4×円周率であり、正十角形の辺の長さの合計よりも長い。従って、円周率は12.3÷4=3.075以上である。

よって、円周率は3.05より大きい。(証明終)

あとがき

いかがでしたでしょうか。

当初は正十二角形を用いて証明を試みて苦戦していましたが、正十角形に登場する黄金比の性質を用いることで初等教育の範囲内での証明が比較的容易にできることに気づき証明を行うことができました。できそうだと思った方はぜひ正十二角形を用いて証明してみてください。

それでは。

追記

記事を書き終わった後に参考文献や資料を検索した際、既に初等教育の範囲内で証明を行っていた方を発見したので紹介させていただきます。

引用　 http://www.suguru.jp/semi/pi/pi/pi1.html

細部こそ違いますが同じ正十角形を用いた証明であり、また因数分解を視覚的にわかりやすくするため長方形を用いるという非常によく似た解法となっており、また細かく解説されているので是非ご覧になってください。