距離化不可能な位相で入門（？）する距離空間
どうも
こんにちは ごててんです 喉が渇きました
位相、みなさまのご家庭にも1,2個あると思いますが 今回はその位相を扱っていきます
この記事の目標は「距離化可能でない位相空間の例」を1つ紹介することです
...だったのですが ちゃんと距離空間の部分を書いてみたら 位相の登場が相当後になってしまいました 距離空間を3秒でも勉強したことがある人は本編から読んでください（） 多分距離空間の部分より短いですが
具体的な予備知識 → 集合, 写像, 直積, 集合族, ユークリッド空間, 三角不等式, (開集合)
この記事では$0$を自然数に含めません（含める派ですが）
記事の流れ
はい それなりにわかりにくい構成になると思うので ここで記事の流れをまとめておきます
距離空間を定義 → 開集合を定義 → 位相空間を定義 → 距離化可能を定義 → 本題 → 距離空間の性質を調べる → 距離化できない例を証明
といった構成になっています
ちなみに連続写像,コンパクトは扱いません この記事では使わないので...
距離空間を定義する
位相空間は幾何チックな空間のことだと 私は認識していますが その中でも身近だと思いやすい幾何の対象である距離空間を定義していきます
数学で距離とよばれるものはふつう ユークリッド空間の中の2点に対して与えられる数値であったわけです
例えば 平面上の2点 $(0,0)$,$(1,2)$の間の距離は$ \sqrt{5}$ であるといったように 「2つの点」に対して「実数」が対応しています これはユークリッド平面の直積$\mathbb{R}^2 \times \mathbb{R}^2$から実数$\mathbb{R}$への写像 $d: \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R} $だとおもうことができ $d((0,0),(1,2))=\sqrt5$ などと書くことができます このようにして定めた$d$の代表的な性質を下にまとめておきます（証明はしません）
$\mathbb{R}^2$で定義された通常の距離$d: \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R} $と任意の$\mathbb{R}^2$上の点$x,y,z$について次が成立する.
$(1)$ $d(x,y) \geq 0 $であり, $d(x,y)=0 $であることと$x=y$であることは同値.
$(2)$ $d(x,y)=d(y,x)$
$(3)$ $d(x,y)+d(y,z) \geq d(x,z)$ （三角不等式）
さて 真面目な雰囲気を漂わせ続けてしまったので 少しずつ壊していきたいのですが（数学の記事とは）
上の主張をみると ユークリッド空間の要素は$\mathbb{R}^2$の部分のみだと思えてくる気がしてきます 気がしてきます 気がしてきます また 上の条件さえ満たせばいわゆる「距離」だと思えるんじゃないか？とも思えてきます 思えてきます 思えてきます この直感を定義に落とし込みましょう
$X$を空でない集合, $d: X \times X \rightarrow \mathbb{R} $を写像とする. このとき以下を満たすなら組$(X,d)$は距離空間であるといい, $d$は距離関数であるという.
任意の$X$の元$x,y,z$について次が成立する.
$(1)$ $d(x,y) \geq 0 $であり, $d(x,y)=0 $であることと$x=y$であることは同値.
$(2)$ $d(x,y)=d(y,x)$
$(3)$ $d(x,y)+d(y,z) \geq d(x,z)$ （三角不等式）
具体例を見てみます
$X$を任意の空でない集合とするとき 関数$d$を以下のように定めます
$x,y\in X$に対して $$d(x,y)= \begin{eqnarray} \left\{ \begin{array}{l} 1 \hspace{5pt} (x\ne y)\\ 0 \hspace{5pt} (x = y). \end{array} \right. \end{eqnarray}$$
すると これは距離になります（証明はしません）
この例から距離っぽさを感じてみましょう 違う点なら$1$遠いという感覚は極端な距離といった感じです また（これは後天的な感覚ですが）点からの距離が$0.1$未満のものがなにもない！という様相は離散的な印象を受けます 離散的な印象を受けるので いやー離散的ですね 実に離散的です
さらにこの例でどんな（空でない）集合にも距離の構造を入れようと思えば入れられるということがわかりました 距離空間は豊富に存在します
実数全体$\mathbb{R}$は, 差の絶対値をとる写像（以後$f$と書きます）を考えると距離空間となります. $-3$と$8$の距離は $f(-3,8)=|-3-8|=11$ となります. （まぁ1次元のユークリッド距離なのですが...）
いや～～～～～ 距離にしか思えませんね 距離にしか思えない
ユークリッド空間と一緒に出されたら間違えちゃうかもしれないですね 映す価値なしになってしまいそうです
上の例1 は空でない集合なら入れられる構造でした この集合は実数全体でもいいので 離散的な実数全体の距離空間$(\mathbb{R},d)$を考えてよいわけです この空間は何者であるのかは上のイメージと同じで すべての点が離れている空間であると考えられます 例2の空間$(\mathbb{R},f)$では $1$と$7$のペアと比べれば $3$と$4$のペアのほうが「近い」という 自然な感覚が距離関数によって入れられていますが 例1の空間では異なる数同士の距離がすべて同じであるので この感覚を持ち出すことができません ここから距離空間は距離関数の選び方次第で同じ集合であっても全く違う構造となりうるということがわかります
近傍・開集合
こうして距離空間の導入が終わりました 距離といえばコレ！ といった感じの概念を調べていきたいと思います
$(X,d)$を距離空間, $\epsilon$>0 とするとき, $X$の点$x$（距離空間における元のことを点とよぶ.）に対して $ N_{\epsilon}(x) = \{\hspace{3pt} y \in X \hspace{3pt}|\hspace{3pt} d(x,y) < \epsilon \hspace{3pt} \}$と定め, これを点$x$の$\epsilon$-近傍とよぶ.
距離が～未満の点を集めてきたものを定義しました 近傍という感じがしますね します
一般的な球とも思えそうです（？）
例2の距離空間$(\mathbb{R},f)$で考えると, 例えば$N_{\epsilon}(1)=(1-\epsilon,1+\epsilon)$(開区間)となります
ユークリッド空間$\mathbb{R}^3$での通常の距離で考えると, $x=(0,0,0)$とすれば$ N_{1}(x)$は中身が詰まっていて境界がない単位球のことです. 確かに原点の近傍といった感じがします
例1の$(X,d)$で考えると, 例えば$X$の点$x$に対して $N_{0.1}(x)=\{x\},$ $N_{2兆}\hspace{2pt} (x)=X$ が成立します. わかりやすいですね. $1$が境目になっています.
準備が整いました 開集合を定義していきます 開集合がこの記事の主役です 開集合は世界を救います（？）
$(X,d)$を距離空間, $A \subset X$, $a \in X$とするとき, $\epsilon >0$があり$N_{\epsilon}(a) \subset A$ となるなら$a$は$A$の内点であるという. また, $A$の内点全体を$A^i$ と書く.
$(X,d)$を距離空間, $A \subset X$とするとき, $A=A^i$が成立するなら$A$は開集合であるという.
内点と開集合は2変数以上の解析学や複素解析の本を開けばよく見られるワードで 実数がもとになっている集合の通常の距離において 内点は「しっかり中に入っている点」, 開集合は「境界が含まれていないもの」というイメージがあると思います ぼくが持っているだけの可能性もありますが...
そのイメージでいけば上も納得できると思います 内点の定義に関しては全く同じですし
開集合の定義も$A \subset A^i$ が成立していると考えれば「$A$のすべての点が$A$内の近傍で囲める」と読めます 一般的な開集合の雰囲気がありますね（本当か？）
＜補足＞
$A$の内点は明らかに$A$に含まれるため $A^i \subset A$は常に成立しています よって開集合であることは$A \subset A^i$であることと同値になります！
直感的には明らかな次の命題が成立します ちゃんと証明してみましょう（と思いましたが、初見なら証明をちゃんと読まなくていいかもしれません 文字で読むのはしんどいので）
$(X,d)$を距離空間, $\epsilon>0$, $x \in X$とするとき, $N_\epsilon(x)$は開集合である.
証明のイメージ図を載せておきます 証明と照らし合わせてみるといいかもしれません
ε近傍が開集合になることのイメージ
$y \in N_\epsilon(x)$を任意にとるとき, これが$N_\epsilon(x)$の内点であればよい. $d(x,y)<\epsilon $であるので, $D=\epsilon -d(x,y)$ とすればこれは正の数となる. このとき, $N_D(y) \subset N_\epsilon(x)$ であることを示せば, 内点であることがわかる. $z \in N_D(y)$とするとき,$d(y,z)< D=\epsilon -d(x,y)$であり, 三角不等式から$d(x,z) \leq d(x,y)+d(y,z)< \epsilon$がわかり, $z\in N_\epsilon(x)$がわかった. したがって, $N_D(y) \subset N_\epsilon(x)$であり,$N_\epsilon(x)$は開集合となる.
距離空間における開集合のイメージが少しずつ湧いてきましたでしょうか？ 距離空間の話題は次の命題を示し注意をある程度述べたら一旦終わりにしたいと思います
この命題は 開集合の性質で最も見る機会が多いと思います... なぜでしょうかね
$(X,d)$を距離空間, $\mathcal{O}$を$(X,d)$の開集合全体（これを開集合系とよぶ）とするとき, 次の$(1)$-$(3)$が成立する.
$(1)$ $X,\emptyset \in \mathcal{O}.$
$(2)$ $O_1 , O_2 \in \mathcal{O}$ とするとき, $O_1 \cap O_2 \in \mathcal{O}.$
$(3)$ $\{ O_{\lambda} \}_{\lambda \in \Lambda}$ を$\Lambda$を添え字とする$X$の開集合族とするとき,
$$
\hspace{15pt} \bigcup_{\lambda \in \Lambda} O_{\lambda} \in \mathcal{O}.
$$
$(1)$ $x\in X $とするとき, 例えば$N_1(x)$は$X$に含まれる. よって, $X$は開集合. $\emptyset$が開集合であることを示す. $\emptyset$の任意の元が$\emptyset^i$の元であればよいが, 空集合から元をとる全称命題は真であるので, 成立する. よって, $\emptyset$ は開集合.
$(2)$ $O_1 , O_2 \in \mathcal{O}$ とする. $x \in O_1 \cap O_2$なら $x \in O_1$であるので $D_1>0$がとれ, $N_{D_1}(x)\subset O_1$. $x \in O_1 \cap O_2$なら $x \in O_2$であるので $D_2>0$がとれ, $N_{D_2}(x)\subset O_2$. このとき $D=\min\{D_1 , D_2\}$ と定めると$N_{D}(x)\subset N_{D_1}(x)\subset O_1$, $N_{D}(x)\subset N_{D_2}(x)\subset O_2$であり, $N_{D}(x)\subset O_1 \cap O_2$ がわかった.
$(3)$ $\{ O_{\lambda} \}_{\lambda \in \Lambda}$ を$\Lambda$を添え字とする$X$の開集合族とする. $\displaystyle x \in \bigcup_{\lambda \in \Lambda} O_{\lambda}$ なら $\lambda \in \Lambda$をとり $x \in O_{\lambda}$とできる. このとき$D>0$ がとれ $N_D(x) \subset O_{\lambda}$ であるので, $\displaystyle N_D(x) \subset O_{\lambda} \subset \bigcup_{\lambda \in \Lambda} O_{\lambda}$がわかった.
帰納的に$O_1 ,\cdots, O_k \in \mathcal{O}$ とするとき, $O_1 \cap \cdots \cap O_k \in \mathcal{O}$ となることもわかります.
$\{ O_{\lambda} \}_{\lambda \in \Lambda}$ を$\Lambda$を添え字とする$X$の開集合族とするとき,
$$
\hspace{15pt} \bigcap_{\lambda \in \Lambda} O_{\lambda}
$$
を考えると, 一般にこれは開集合となりません.
例2の状況（実数の差の絶対値で入れた距離）で考えると,
$$
\hspace{15pt} \bigcap^{\infty}_{n=1} (-\frac{1}{n} , 1+\frac{1}{n}) = [0,1]
$$
となり, これは開集合ではありません.（$0$と$1$が$[0,1]$の内点でない）
位相空間
我々は様々な空間を彷徨い旅を続けてきた 初めに見たものは「ユークリッド平面」
3つの性質（命題1）が私達を迎え入れてくれた その中に我々は「距離空間」を見出し さらなる旅を続けた
距離空間の中で一般化された「開集合」が飛び交う中 ついに新たな3つの性質（命題3）にたどり着く
そこで我々が見たものとは...？
...
↑深夜に書きました さて ついに位相空間です 命題1からユークリッド平面の要素を削ったように 命題3から距離空間の要素を削っていこうと思います †そしてたどり着いたのが†... なんでもないです
命題3をよく見てみると, 3つの性質はある集合の 部分集合族 について言っていると考えられます
$X$に距離が入ってなくても いいんじゃないですかね～～～～ ということで 位相空間の定義を次で与えます
$X$を空でない集合, $\mathcal{O}$を$X$の部分集合を元とする集合（$X$の冪集合$2^X,P(X)$の部分集合のこと）について, 次の$(1)$-$(3)$が成立するとき, $X$,また組$(X,\mathcal{O})$を位相空間とよび, $\mathcal{O}$の元を開集合, $X$の元を点とよぶ.
$(1)$ $X,\emptyset \in \mathcal{O}.$
$(2)$ $O_1 , O_2 \in \mathcal{O}$ とするとき, $O_1 \cap O_2 \in \mathcal{O}.$
$(3)$ $\{ O_{\lambda} \}_{\lambda \in \Lambda}$ を$\Lambda$を添え字とする$\mathcal{O}$の元の族とするとき,
$$
\hspace{15pt} \bigcup_{\lambda \in \Lambda} O_{\lambda} \in \mathcal{O}.
$$
いや～～～ 命題3を少し改変するだけでいいので定義がラクでした というのはどうでもよくて こうして位相空間を定義できたわけです 距離空間の開集合系は上の性質を満たしていたので 距離空間は位相空間に包含されることがすぐわかります 位相空間の世界は広い！（適当）
距離空間から開集合の性質を抜き出して考えたのが位相空間ですよ～～～ といったように書いてしまいましたが なぜ開集合を考えるといいのか, という部分をごまかしにごまかしています 開集合を考える理由の1つは連続写像にあります 基礎的な解析学における連続性を位相空間論では開集合を用いて書き直します すると開集合を考えることで空間における連続性を考えることができます
$(X,d)$を距離空間, $\mathcal{O}_d$をその開集合系とするなら $(X,\mathcal{O}_d)$は位相空間である.
みなさまお気づきの通り 抽象度がかなり増してきました 「想像する」ことが難しくなってきています 開集合の定義に「境界が含まれていないもの」というニュアンスを感じることは もう難しいです
イメージしにくい具体例を見て さらに距離のニュアンスを破壊していきましょう
$X$を空でない集合, $2^X$をその冪集合とするとき $(X,2^X)$は位相空間である.
明らかに位相空間になります 真剣に証明しようと位相空間の定義を確認すると笑ってしまう程度には明らかです さて イメージしてみましょう 開集合は近傍のニュアンスを持っています（位相空間における近傍の定義は異なりますが, この言葉をちゃんと定義せずに使います（おい）） 点$x \in X$を含む開集合として$\{ x \}$があります この開集合の存在にイメージを膨らませてみましょう 点$x$を$x$以外の点が入らないように囲むことができていると考えられそうです さらにこれはどんな点でも可能でした するとどうでしょう $(X,2^X)$が急にスカスカな空間を表していると思えてこないでしょうか 実に離散的です 離散的です 離散的です というわけでこの位相は離散位相と呼ばれています
$X$を空でない集合とするとき $(X,\{\emptyset ,X\})$は位相空間である.
こちらも明らかに位相空間になります イメージしてみましょう 点$x \in X$を含む開集合は$X$しかありません！ 1つを囲もうとすると全部入ってきてしまいます 点$x$のすぐ近くにすべての点が密集していると考えられそうです というわけでこの位相は密着位相と呼ばれています
なんかそれっぽい図
距離化可能とは
やっと距離化可能の定義ができるぞ～～～～～！ うれしい～～～ うれしい では早速距離化可能の定義をします！！！
$(X,\mathcal{O})$を位相空間とするとき, 距離空間$(X,d)$があり, その開集合系$\mathcal{O}_d$が$\mathcal{O}=\mathcal{O}_d$ となるなら $(X,\mathcal{O})$は距離化可能であるという.
距離化可能でないとき, 距離化不可能であるといいます（一応）
なかなかイメージしにくい定義です 具体的な位相空間をみたとき 距離化可能っぽいな～～ 距離化不可能そうだな～～ などと考えることは簡単にできなさそうです 考えやすい例を出してみます
離散位相$(X,2^X)$は例1の距離空間$(X,d)$で距離化可能である.
$(X,d)$の開集合系が$2^X$と一致することを示せばよい. $x\in X$とすると$N_{\frac{1}{2}}(x) \subset \{x\}$ であるから, $\{x\}$は開集合. $A \subset X$ とすれば $\displaystyle A = \bigcup_{x \in A} \{x\}$であるから, $A$は開集合. したがって, 任意の$X$の部分集合は開集合であることがわかった.
密着位相$(X,\{\emptyset ,X\})$は距離化不可能である.
$(X,d)$を開集合系が密着位相と一致する距離空間であるとすると, $\epsilon>0$に対して点$x \in X$の近傍$N_{\epsilon}(x)$は開集合であるが, $x$を含むため空集合ではない. よって, $N_{\epsilon}(x)=X$. $y \in X$ $(x\ne y)$とすると $0< d(x,y)<\epsilon$ が成立しているが, $\epsilon>0$の任意性より $d(x,y)=0$となり矛盾.
距離化可能であるのはたいへんにうれしいものです なぜなら距離空間で成り立つ性質がすべて使えるからです
本題
はい 本題です ここから読んでください！（え）
早速ですが目的の位相空間を定義します
$n>0$を整数とするとき, $O_n=\{1, \cdots , n\}$ と定め,
$\mathcal{O}_{\mathbb{N}} = \{ \emptyset , \mathbb{N} \} \cup \{ \hspace{3pt} O_n \hspace{3pt} | \hspace{3pt} n>0 $は整数$\}$ と定める. (このとき, $(\mathbb{N},\mathcal{O}_{\mathbb{N}})$は位相空間となる.)
位相空間となることを示します
共通部分がまた開集合となることを示す. 少なくとも一方が$\emptyset , \mathbb{N}$であるときはすぐわかる. $O_n , O_m$の共通部分を考える. $n \geq m$を仮定してよい. このとき$O_n \cap O_m = O_m$ からこれは開集合. 集合族の和集合がまた開集合となることを示す. $\mathbb{N}$が含まれていれば開集合になるとわかる. よって, 空集合と$\mathbb{N}$はないと考えてよい. $\Lambda$を任意の集合とするとき, 写像$f: \Lambda \rightarrow \mathbb{N}$を定めて集合族を$\{ O_{f(\lambda)} \}_{\lambda \in \Lambda}$ と書くことができる. $N=\sup\{ \hspace{3pt} f(\lambda) \hspace{3pt} | \hspace{3pt} \lambda \in \Lambda \hspace{3pt}\}$ と定めるとき（無限大も許す）, $N=\infty$なら $\displaystyle \bigcup_{\lambda \in \Lambda} O_{f(\lambda)} = \mathbb{N}$である. $N<\infty$ のとき $\displaystyle \bigcup_{\lambda \in \Lambda} O_{f(\lambda)} = O_N$となることを示す. まず$N=\max\{ \hspace{3pt} f(\lambda) \hspace{3pt} | \hspace{3pt} \lambda \in \Lambda \hspace{3pt}\}$ であることを確かめる. $A=\{ \hspace{3pt} f(\lambda) \hspace{3pt} | \hspace{3pt} \lambda \in \Lambda \hspace{3pt}\}$としたとき, $a \in A$があり$0 \leq N-a< \frac{1}{2}$が成立する. $N-a$は整数であるから, $N-a=0$で$N=a$.したがって, $N \in A$がわかり$N = \max A$がわかった. これを用いると, $\lambda _N \in \Lambda$がとれて $N=f(\lambda_N)$ とできる. すると, $\displaystyle \bigcup_{\lambda \in \Lambda} O_{f(\lambda)} \subset O_{f(\lambda_N)} $ であるので $\displaystyle \bigcup_{\lambda \in \Lambda} O_{f(\lambda)} = O_{f(\lambda_N)} = O_N$ となることがわかる.
さて 位相空間であることが証明できました この空間についてイメージしてみましょう 自然数$1,2$からみた$3$を考えると 「$1$と$3$が入っている開集合の全体」と「$2$と$3$が入っている開集合の全体」が一致することから $1$と$3$ との距離と$2$と$3$ との距離がほぼ一致していそうな気がしてきます さらに自然数$1,2,3$からみた$4$を考えると これもそれぞれ距離がほぼ一致していそうな気がしてきます 別のアプローチで考えます 「$1$と$2$が入っている開集合の全体」の方が「$1$と$3$が入っている開集合の全体」より多いことから $1$に近いのはどちらかといえば$2$ とイメージできます また$3,4,5,6,\cdots$ はどんどん$1$から離れていく列だとイメージできます もしこういうイメージ通りの距離空間があったら素敵ですね！ ありませんけど！
距離空間はハウスドルフ空間である
距離化不可能であることを示すにあたって 距離化可能であることの必要条件を考えます どう考えればいいかというと 距離空間で成り立つ性質の中でも開集合で記述されるものを考えることで必要条件を考えます つまり性質がいい位相空間を調べるということです ここでは位相空間においても考えやすいハウスドルフ空間の定義をしていきます
$(X,\mathcal{O})$を位相空間とする. $x,y\in X$が異なる2点であれば, 2つの$X$の開集合$U,V \in \mathcal{O}$で $(U \cap V = \emptyset)$であるものがあり$x\in U , y\in V$ とできる（異なる2点が開集合で分離できる, などと説明される）という性質をもつとき, $(X,\mathcal{O})$はハウスドルフ空間であるという.
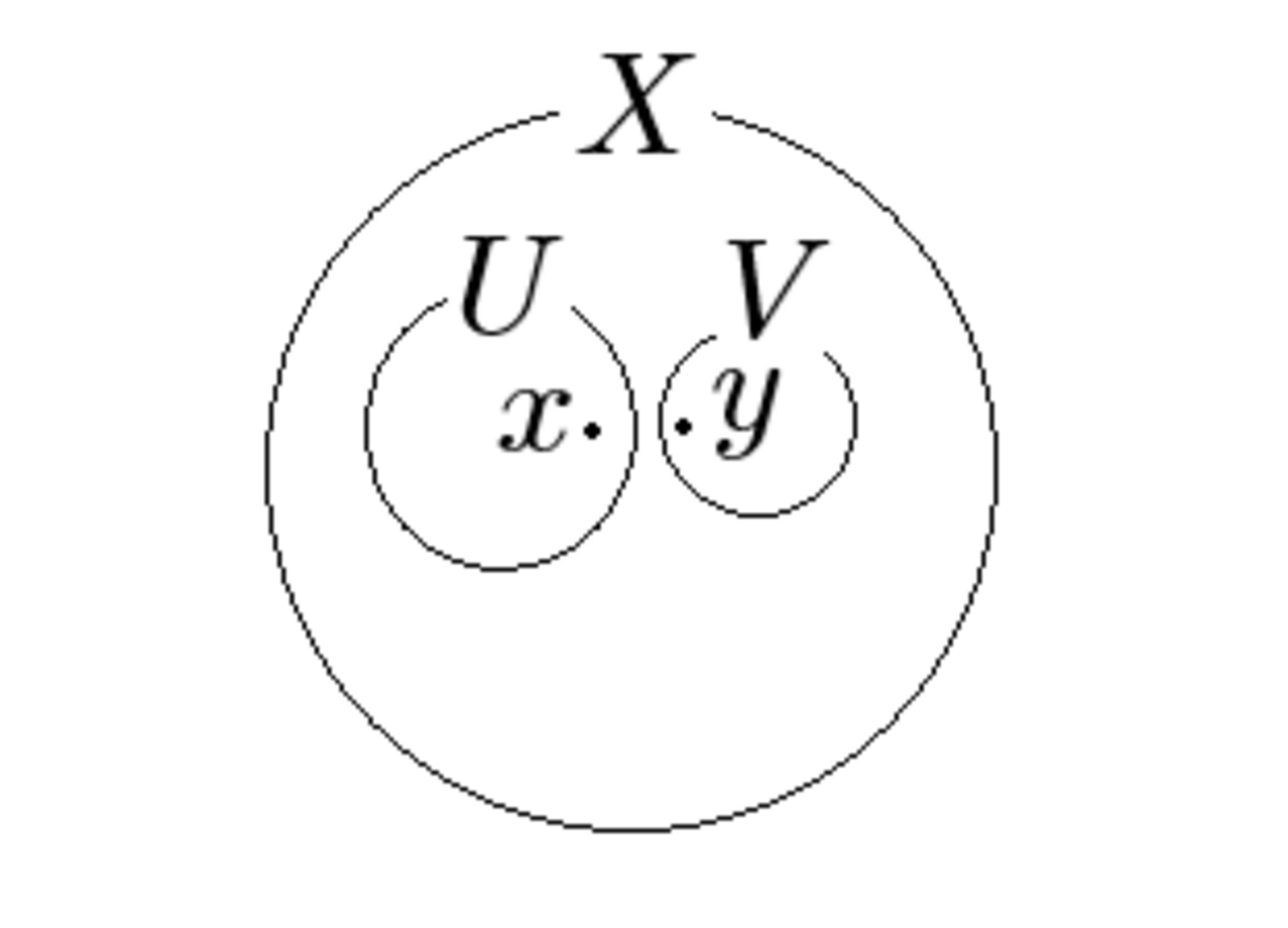世界一わかりやすいハウスドルフ空間の図
人間がすぐ想像できる空間はだいたい持っていそうな性質です そしてこれはすべての距離空間で成り立ちます
距離空間の開集合系はハウスドルフ空間となる.
$(X,d)$を距離空間とする. $x,y\in X$を異なる2点とするなら$d(x,y)>0$であり, $\epsilon = \frac{1}{2} d(x,y)$とすれば, $N_{\epsilon}(x) $と$N_{\epsilon}(y)$は2点を分離する開集合となる. この2つの開集合が共通部分をもたないことを示す. $z \in N_{\epsilon}(x) \cap N_{\epsilon}(y)$ であれば $d(x,z),d(y,z) < \epsilon$ が成立するが, $d(x,z)+d(y,z) < 2\epsilon = d(x,y)$ よりこれは三角不等式に反する.
この定理を使える形にすると下のようになります
距離化可能な位相空間はハウスドルフ空間となる
もうお気づきですね この系の対偶を用いて距離化不可能を示すことができます！
感動のラスト
さて すべての準備が整いました
$(\mathbb{N},\mathcal{O}_{\mathbb{N}})$がハウスドルフ空間でないことを示します！！！！！
$2$が入っていて$1$が入っていない開集合は存在しません！！！！！！！！！！！！！
おわりです！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
ここまで読んでいただきありがとうございました！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！