青雪江1.4節の例題（アイツ）を直感的に理解する

どうも

こんにちは　ごててんです　うまい棒が美味しい季節になりました
代数学2　環と体とガロア理論　という本がありまして　いわゆる青雪江ですが　この本の「1.4 剰余環」にはある例題が存在します　その例題とは...？

ぼく「？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？」

記事の目的

はい　あまりのイメージのできなさに取り乱しました　左辺の集合を見て　これが　${\mathbb{F}}_{17}$ だと思えるなんて...　やっぱり環論は基本的な部分でもう天才専用みたいなところがあるんだな～～～～～　などと思っていました

しかし！　そんなことはありません！！！！！　この記事では　この式が納得感にあふれたものであることを　青雪江に載っているものとは別の証明を与えることで証明してみせます！！！！！！！！！！！！

遅れましたが　この記事の前提知識は青雪江1章程度の基礎的な環論です　有限に長い記事ができてしまうので　この記事では以下の事項を前提知識として　記号は青雪江と同じものを使用します

具体的な前提知識・・・　多項式環　イデアルの生成　環の同型　剰余環

$\mathbb{Z}[\sqrt{-1}]$における$(4+\sqrt{-1})$をかんがえてみるぞ

格子点であそびましょう　$(4+\sqrt{-1})$を視覚的に捉えます　$I=(4+\sqrt{-1})$とするとき　この元を複素平面にプロットします　$a\in I$とするなら $z=x+y\sqrt{-1}\in \mathbb{Z}[\sqrt{-1}]$があり

$a=z(4+\sqrt{-1})=(x+y\sqrt{-1})(4+\sqrt{-1})=x(4+\sqrt{-1})+y(-1+4\sqrt{-1})$

ここから　$I$の元が $4+\sqrt{-1}$と$-1+4\sqrt{-1}$の整数係数の1次結合で書けることがわかりました
逆にこの1次結合で書ければ$I$の元となります　この2つの元は次のような感じです

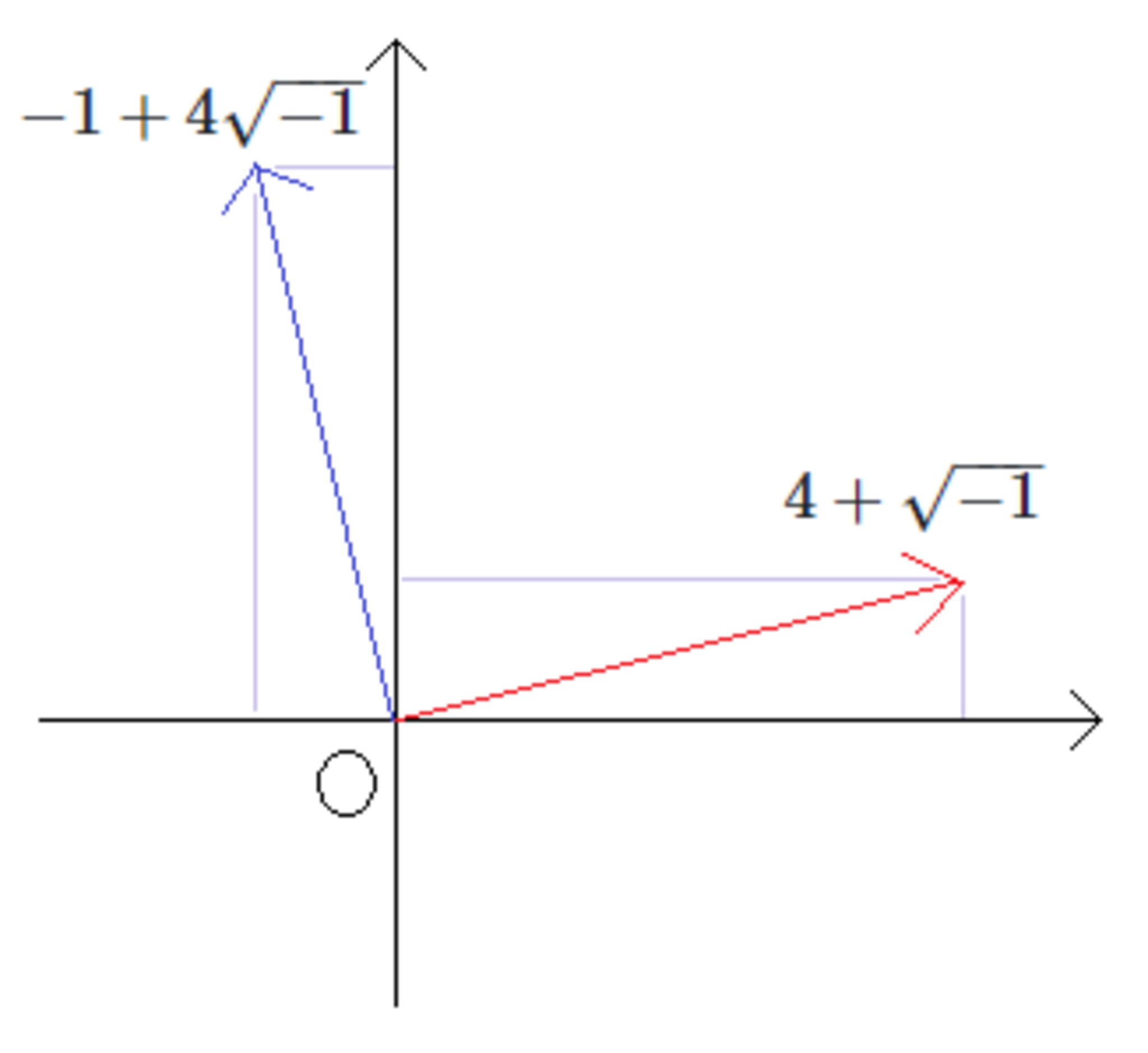この令和の時代にペイントで書いた図

そして　この元を整数回足したものは　下のような感じに広がっていきます

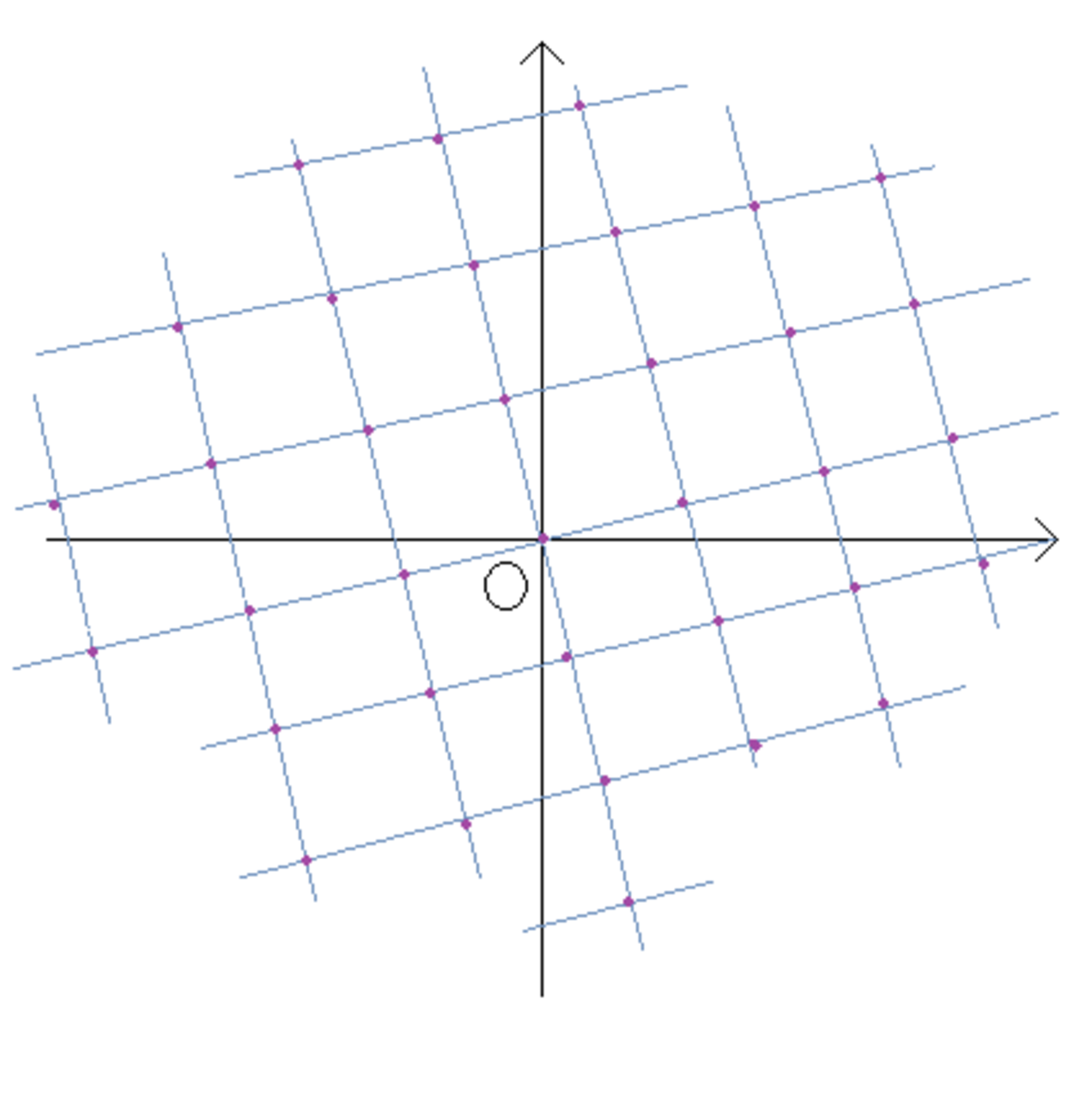結構歪んでるって　ちゃんと描きなさいよ

というわけで　$(4+\sqrt{-1})$がなんとなくイメージできました

$\mathbb{Z}[\sqrt{-1}]/(4+\sqrt{-1})$の元を視覚的に捉える

剰余類はイデアルの元にある共通の元を加えたものの集合です　つまり　上の図の紫色の点を一括で平行移動させたものが剰余類だと考えられそうです

はい　↑は結構無理してアイデアを説明しようとした文なのでわかりにくいですが　続けます（

$a+(4+\sqrt{-1})\in \mathbb{Z}[\sqrt{-1}]/(4+\sqrt{-1})$ がどういう点の集まりなのかを考えます

例えば $a=1$ の場合　つまり$1+(4+\sqrt{-1})$を考えてみます
これは図2の紫の点を右に$1$ずらした（つまり$1$を足した）ものの集合で　下の図の青い点だと思えます

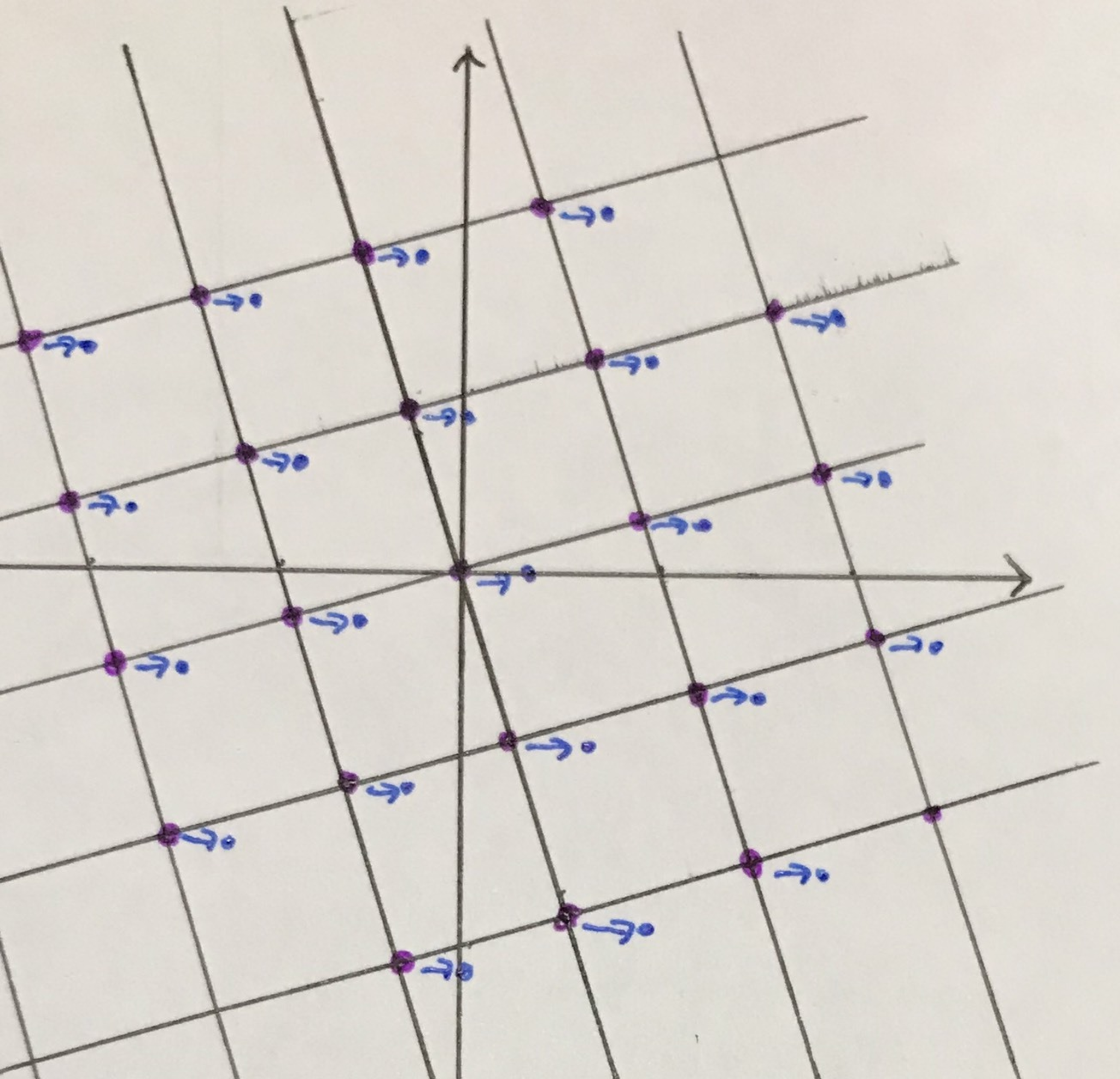急に手書き

点の動きをもっと考えやすく

図3を見ると　ある気持ちが湧いてきます　「正方形1個だけをみればよくない！？」
そうです　この点の平行移動は　正方形を格子の単位として　どこでも同じ様子がみられます

図1のベクトルがこの正方形の辺に対応していることを考えれば　下の図のように　どこにある点も図1のベクトルだけで　1つの正方形の中に押し込めることができます　これより完全代表系が下図の紫の正方形の中だけで構成できるとわかります　安心して正方形の中で議論しましょう

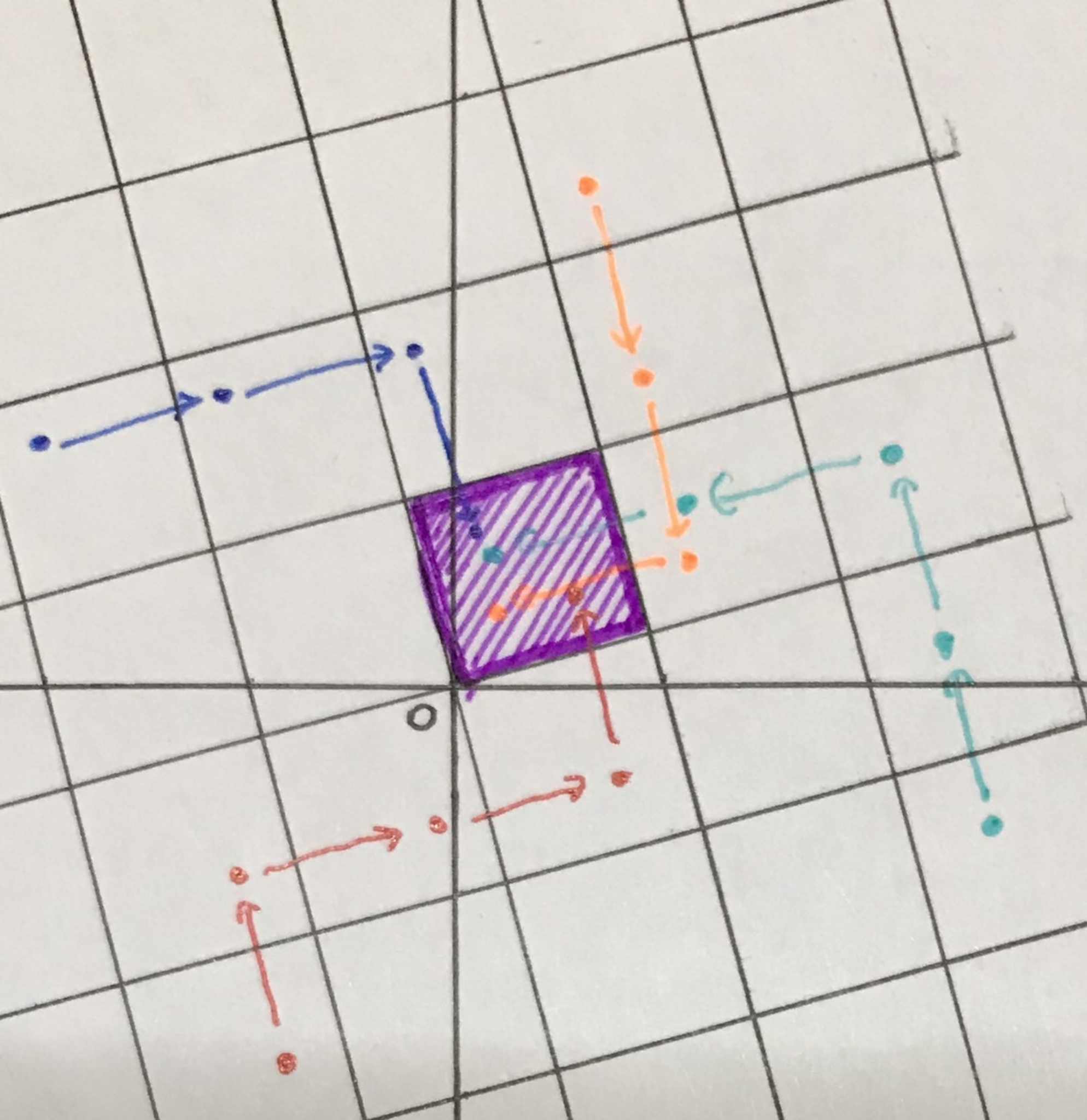三角定規を使って描きました

さて　正方形の中の点を数えてみましょう　16個です
そしてこの正方形の頂点は　同じ剰余類を表しますから　プラスで1個点があります

そう、全部で17個です！！！！！！

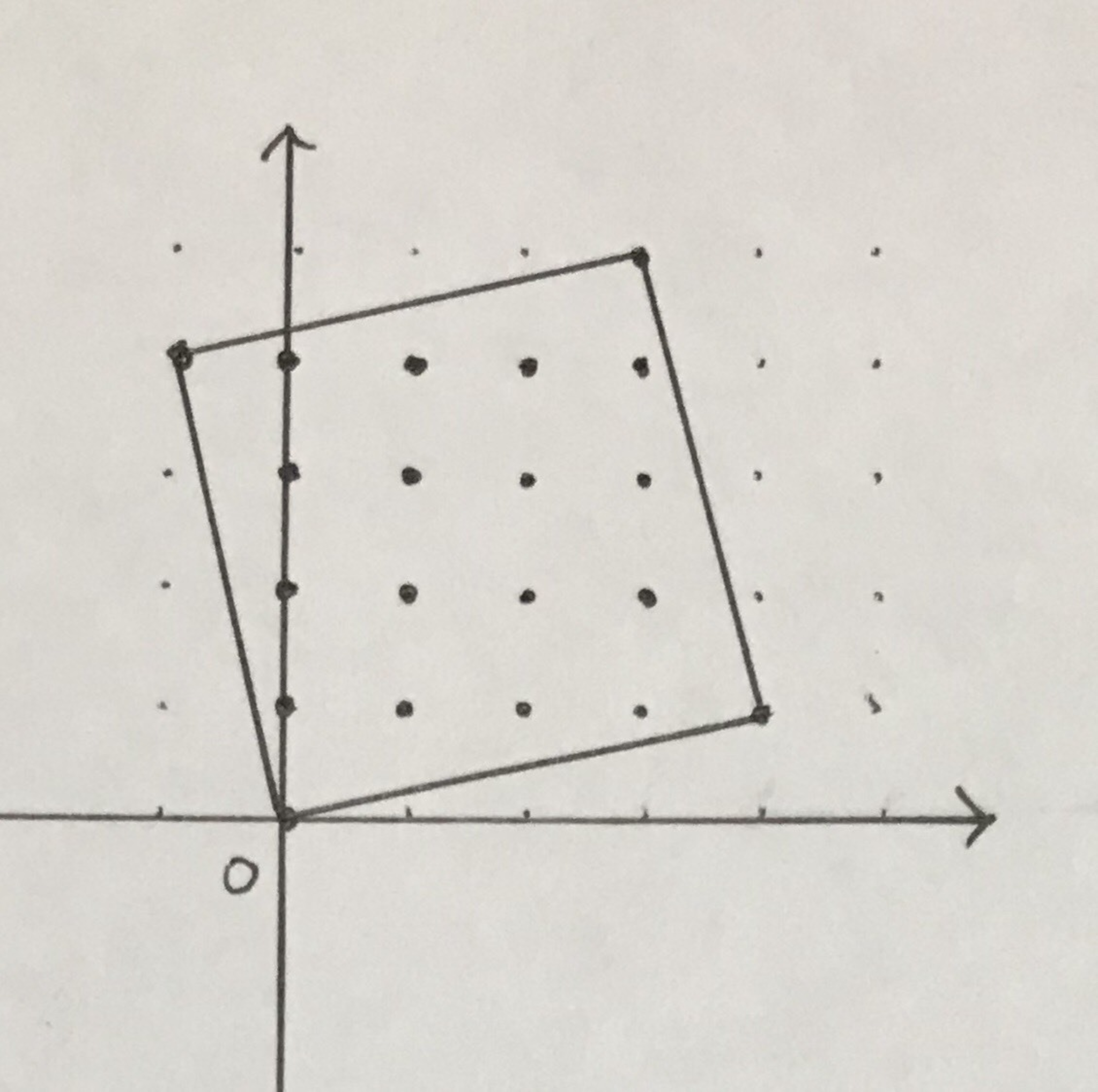正方形の中の点たち

ここで　$1$ずつ足してみる様子を図示すると下のようになります

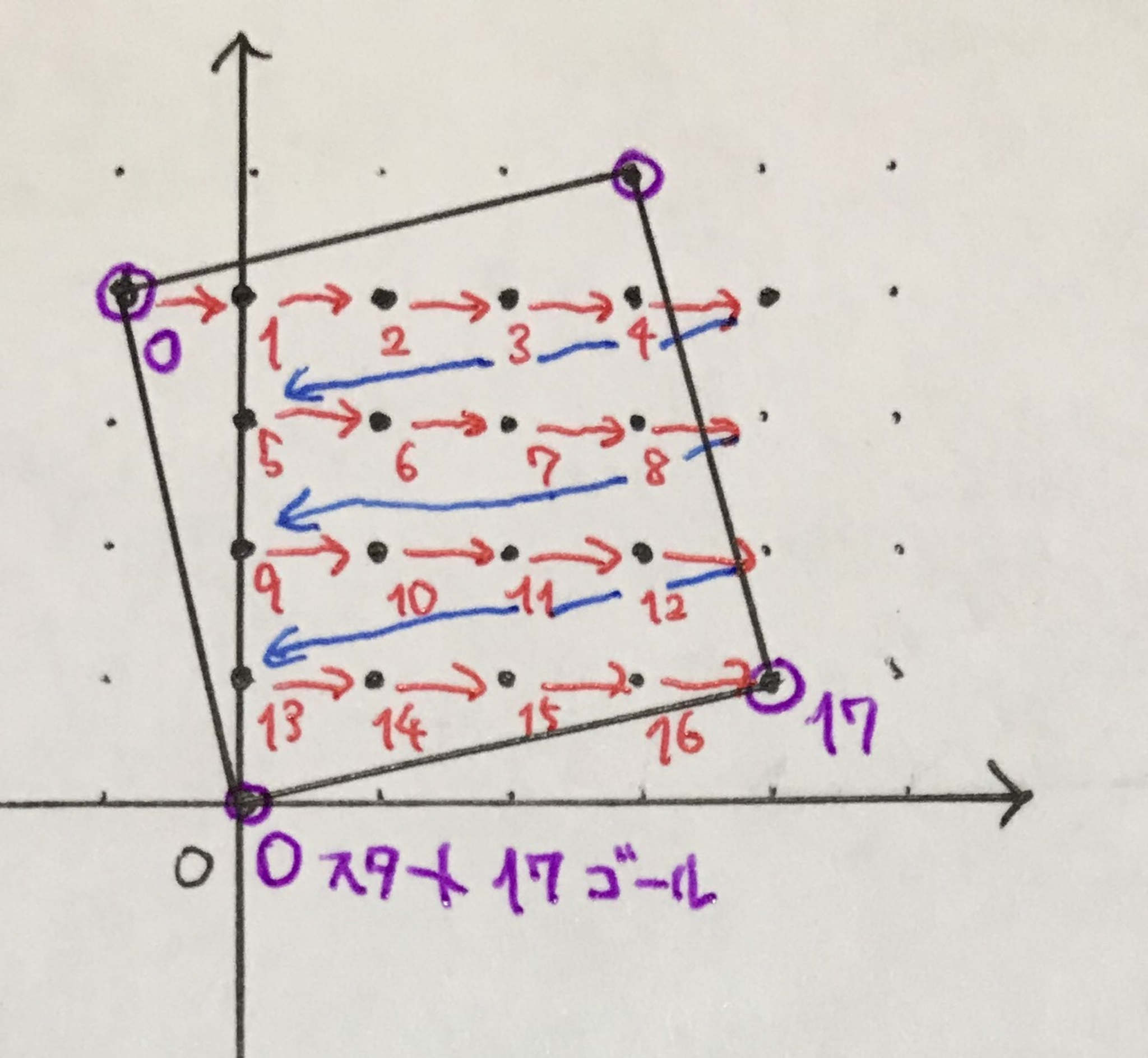がんばって描きました

はい　もう${\mathbb{F}}_{17}$にしか見えません！

まとめ

同型であることの細かい証明は書きませんが　あの難しそうな同型を図の力で理解することができたと思います　人類の勝利を感じますね！！！（言い過ぎ）（感じません）

いや～～～　$\mathbb{Z}[\sqrt{-1}]$のイデアル　美しかったですね　ここまで読んでいただきありがとうございました～～～～