相互情報量による確率変数の独立性判定

離散確率変数$X,Y$が独立であるとき，以下の式が成り立つ。

$ P(x,y)=P(x)P(y) $

この性質を応用しているのが，以下の式で定義される相互情報量$I(X;Y)$である。

$ I(X;Y)=\sum_{y \in Y}\sum_{x \in X}P(x,y)\log{\frac{P(x,y)}{P(x)P(y)}} $

※$\log{0}=0$とする

相互情報量$I(X;Y)$が$0$であるとき，$X,Y$は互いに独立である。

$I(X;Y)=0$　$\Longleftrightarrow$　$X,Y$が互いに独立

同様の使われ方をする概念に，相関係数$r_{XY}$というものがある。

$ r_{XY}=\frac{\sum_{i=1}^{|X|}(X_i-\overline{X})(Y_i-\overline{Y})}{ \sqrt{\sum_{i=1}^{|X|}(X_i-\overline{X})^2\sum_{i=1}^{|X|}(Y_i-\overline{Y})^2}} $

しかし，こちらは以下のみが成り立つため，一般に独立性を調べる用途においては，相互情報量の方が都合の良い場合が多い。

$X,Y$が互いに独立　$\Longrightarrow$　$r_{XY}=0$

例えば，以下のような曲線的な依存関係が$X,Y$間にあった場合，相関係数は$0$に近しい値を示すのに対し，相互情報量は十分大きい値を示す。
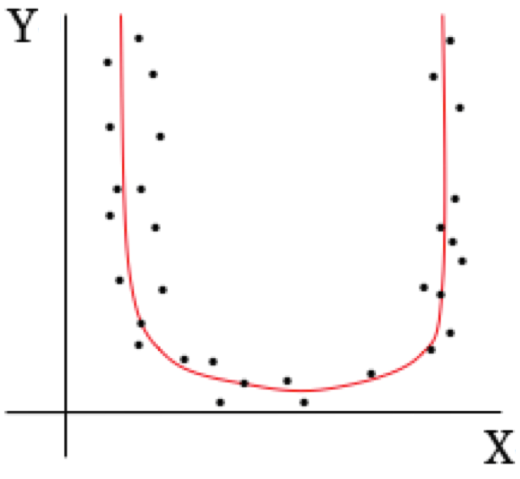XーY間の曲線的な依存関係