RPGの世界は球ではなく………
あなたはRPGをプレイしたことはありますか？
その中で地図はありませんでしたか？
RPGの世界ではしばしば見られるのですが、
$$右端から右に行こうとすると左端から出てくる。$$
$$左端から左に行こうとすると右端から出てくる。$$
$$上端から上に行こうとすると下端から出てくる。$$
$$下端から下に行こうとすると上端から出てくる。$$
というような世界があります。
僕たちは地球に住んでいるので「このRPGの世界は球」だと思うじゃないですか？
違うんですよ。
結論から言うと、このRPGの世界は球ではなくドーナツ型なんです。
それを説明していきます。
目次
- RPGの世界を数式で表す
- 紙は丸めると円柱になる
- 丸めた紙の両端をくっつけるとドーナツ型になる
RPGの世界を数式で表す
RPGの世界を座標で表すとこうです。
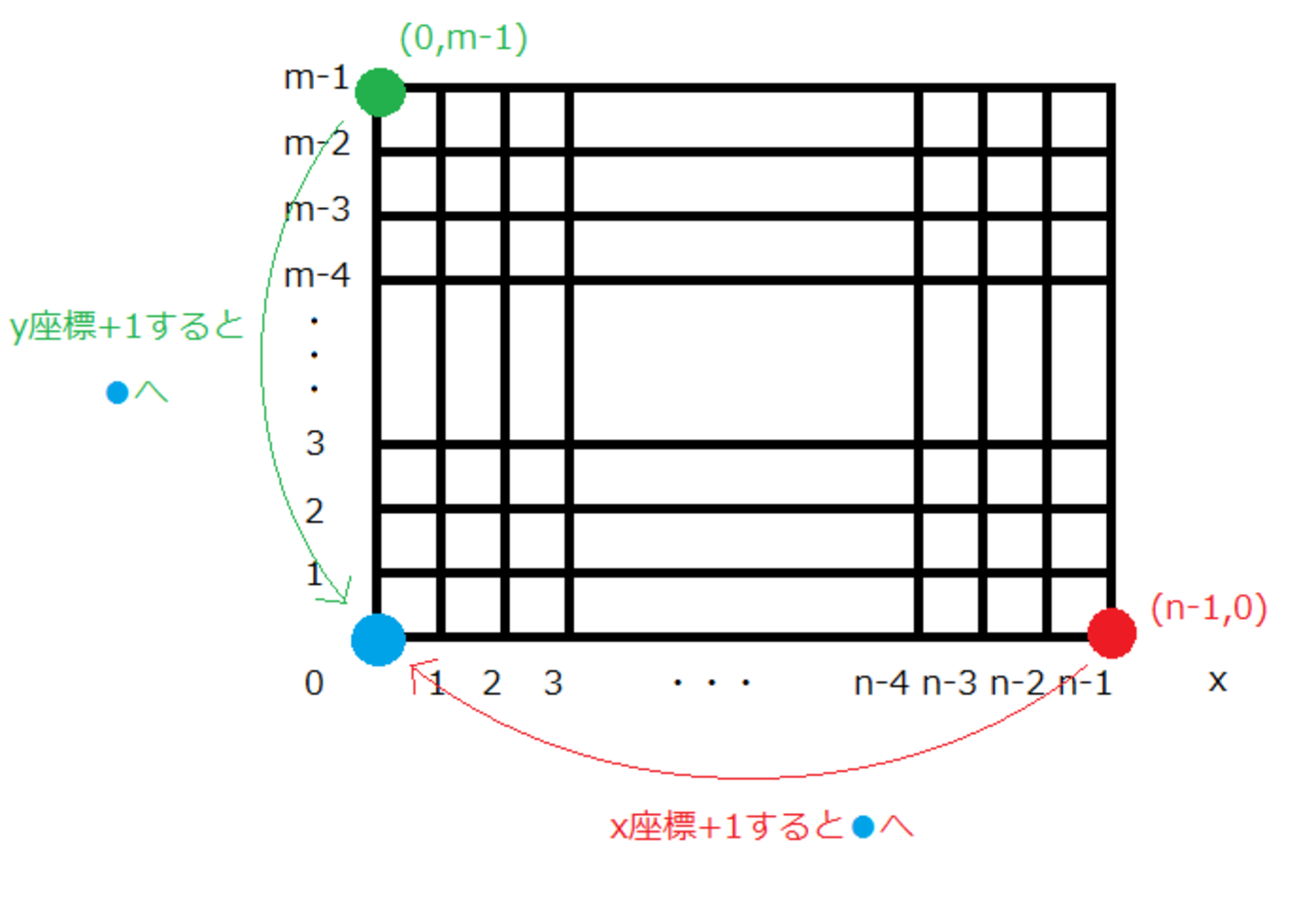RPGの地図
これを数式で表すと、以下のようになります。
$\lbrace (x,y)|x \in Z_{n},y \in Z_{m}, n,m \in \mathbb{N} \rbrace$
$Z_{n}$というのは、$n$で割った余りの集合を表します。
($\mathbb{Z}/n\mathbb{Z}$と表記することもあります。)
例えば、$Z_{5} = \lbrace 0,1,2,3,4 \rbrace$、$Z_{2} = \lbrace 0,1 \rbrace$です。
$Z_{2}$は日常では、スイッチのON/OFFに該当します。
時計は$Z_{12} = \lbrace 0,1,2,3,4,5,6,7,8,9,10,11 \rbrace$ですね。
RPGの地図では、上下左右のループを$Z_{n},Z_{m}$で表現しています。
$x$座標の$Z_{n} = \lbrace 0,1,2,...,n-1 \rbrace$は、$n-1$(右端)で$+1$(右に$1$移動)すると$0$(左端)になります。
また、$0$に$-1$すると$n-1$になります。
$y$座標は$Z_{m} = \lbrace 0,1,2,...,m-1 \rbrace$で$m-1$(上端)に$+1$(上に$1$移動)すると$0$(下端)になります。
紙は丸めると円柱になる
まずは、この地図を丸めて円柱にしたいと思います。
イメージは以下の通りです。
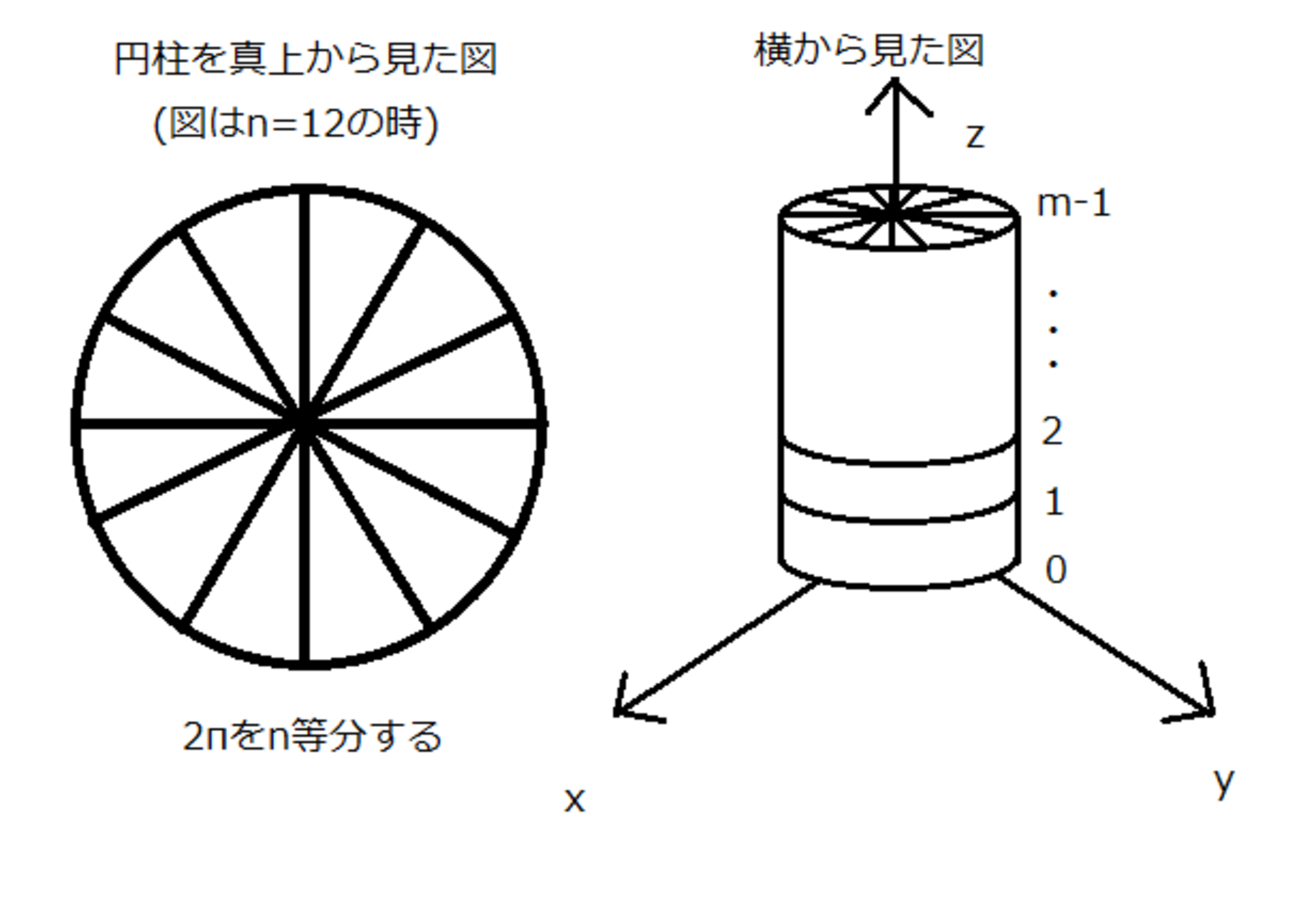RPGの地図を円柱にする
そして、図のように円柱にする操作は以下の通りです。
$$写像f：\lbrace (x,y)|x \in Z_{n},y \in Z_{m}, n,m \in \mathbb{N} \rbrace → \lbrace (cos \frac{2πx}{n},sin \frac{2πx}{n},y) \rbrace
(\subset 円柱の表面： \lbrace {(cosθ, sinθ, z)|θ \in [0,2π], z \in Z_{m}}\rbrace)$$
写像$f$は全単射となり「RPGの地図は円柱と同じ」とみなすことができます。
$2$つの集合に対し、片方の集合からもう片方への集合への全単射な写像が存在することを同型といいます。
この場合、「RPGの地図と円柱の表面の集合は同型」といいます。
全単射については別記事があるので、そちらを見ていただければと思います。
全単射と日常生活での利用
丸めた紙の両端をくっつけるとドーナツ型になる
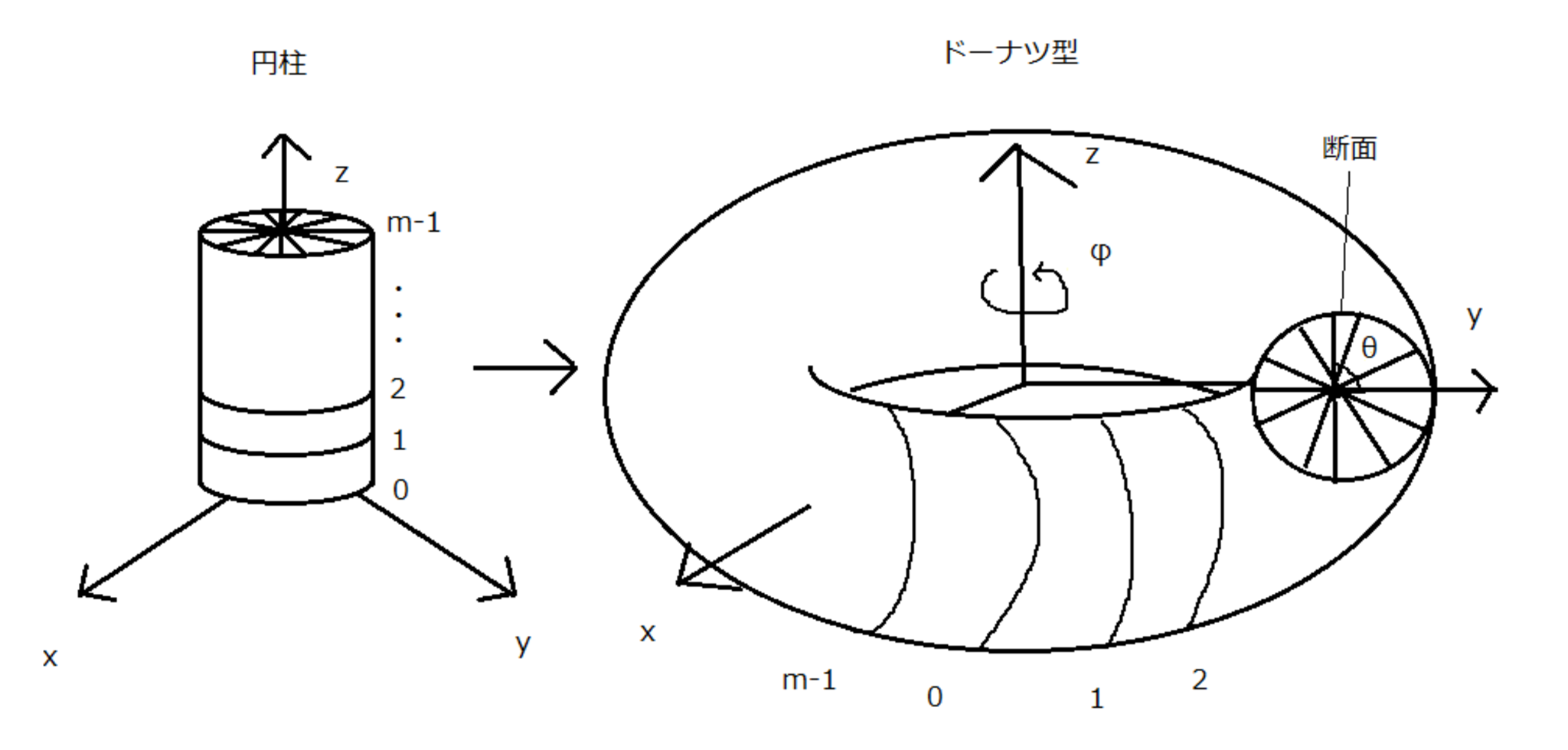円柱をドーナツ型にする
$$
写像g：\lbrace (cos \frac{2πx}{n},sin \frac{2πx}{n},y) \rbrace → \lbrace ((1+cos\frac{2πx}{n})cos \frac{2πy}{m}, (1+cos\frac{2πx}{n})sin \frac{2πy}{m}, sin\frac{2πy}{m}) \rbrace (\subset トーラスの表面：\lbrace ((R+rcosθ)cosφ, (R+rcosθ)sinφ, rsinθ)|R,r\in \mathbb{R^{+}},θ,φ \in [0,2π] \rbrace)$$
写像$g$は全単射となり「RPGの地図を丸めた円柱はドーナツ型と同じ」とみなすことができます。
よって、RPGの地図はドーナツ型ということが言えます。
ちなみに、ドーナツ型ことトーラスは球と同型でないことがわかっているので、RPGの地図は球ではないということも言えます。
補足
ドーナツ型のことを数学ではトーラスといいます。
トーラスの表面の集合は以下のように表せます。
$$\lbrace ((R+rcosθ)cosφ, (R+rcosθ)sinφ, rsinθ)|R,r\in \mathbb{R^{+}},θ,φ \in [0,2π] \rbrace$$
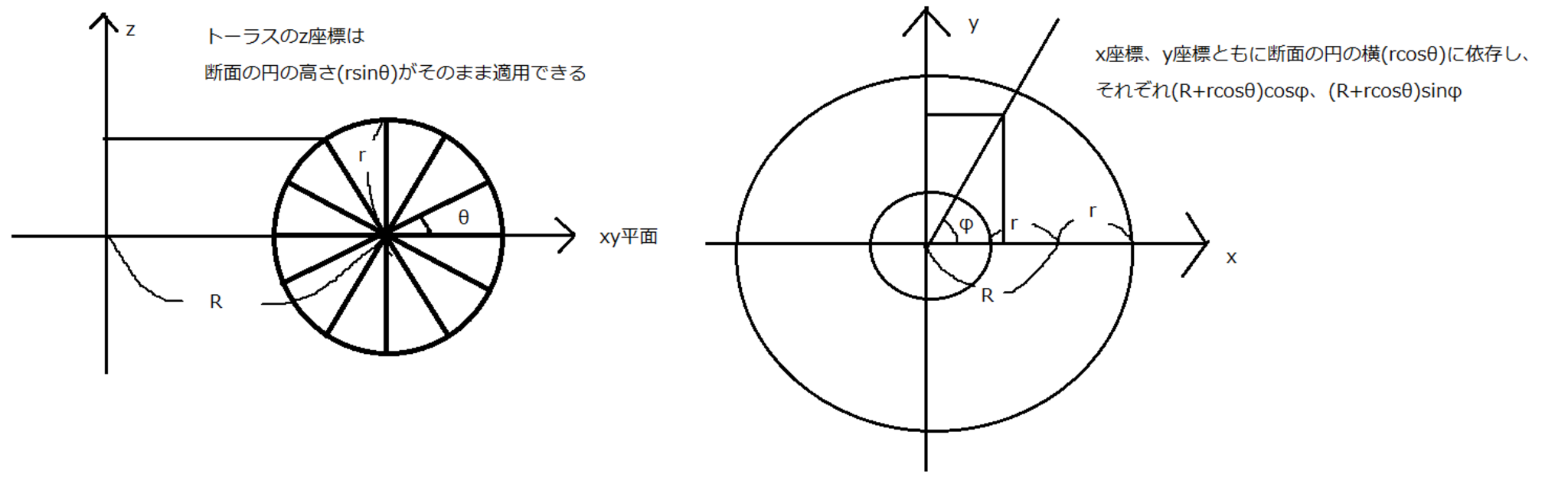考え方
$f,g$では、$R,r=1,θ=\frac{2πx}{n}, φ=\frac{2πy}{m}$を代入しています。