0
自作問題の解答: 反比例曲線と正三角形列
58
0
$$\newcommand{combi}[2]{{}_{#1}\mathrm{C}_{#2}}
\newcommand{disp}[0]{\displaystyle}
\newcommand{dou}[0]{\Leftrightarrow}
\newcommand{mr}[1]{\mathrm{#1}}
\newcommand{permu}[2]{{}_{#1}\mathrm{P}_{#2}}
\newcommand{vec}[1]{\overrightarrow{#1}}
$$
問題: 020
曲線$C$: $y=\dfrac{1}{x}$ ($x>0$) とする。原点、曲線$C$上、$x$軸上に3点があるように正三角形$T_1$をとる。$n=1,2,\dots$ について図のように、$x$軸上に一辺があり、曲線$C$上に一点をもち、正三角形$T_n$に右から一点を共有するように正三角形$T_{n+1}$を定める。$T_n$の曲線$C$上にある点の$x$座標を$t_n$とする。
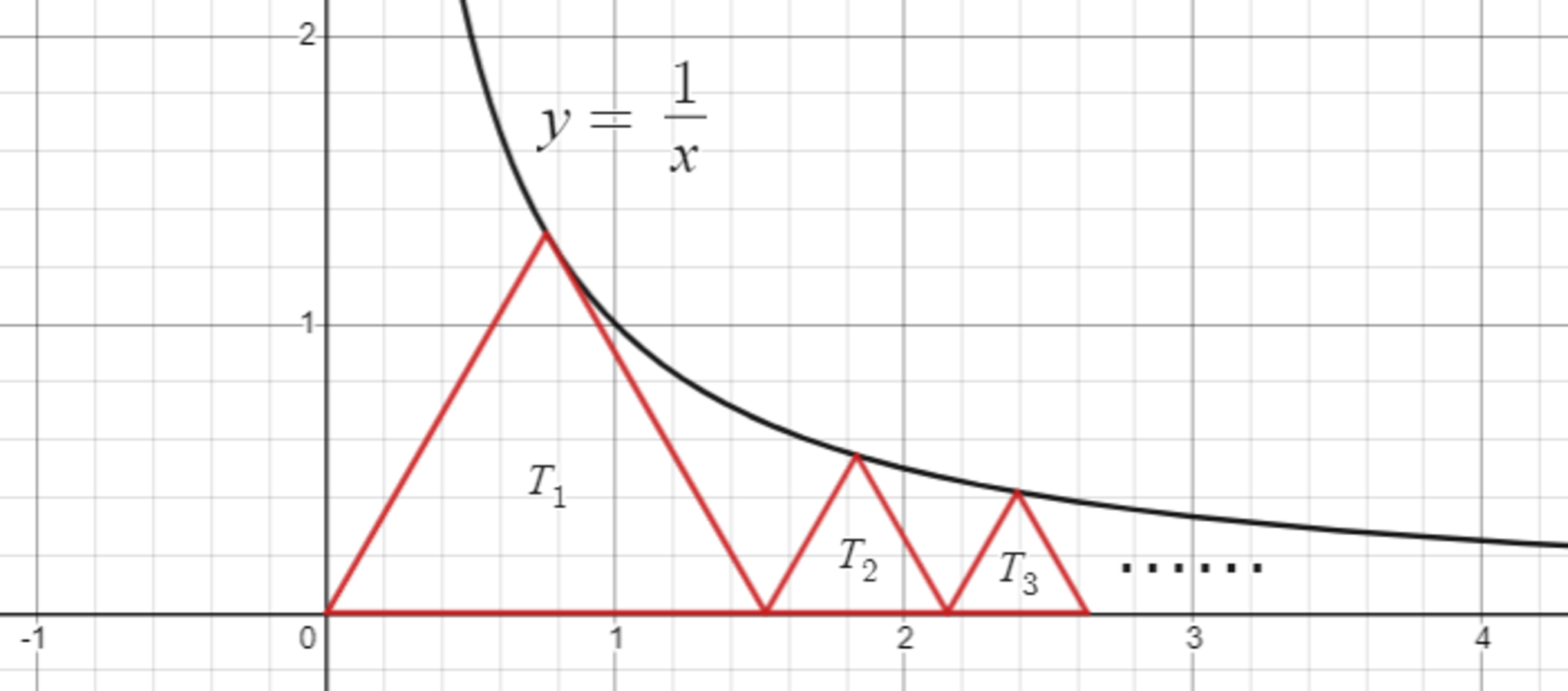
(1) $t_1$を求めよ。
(2) $a_n=t_n+\dfrac{1}{\sqrt{3}t_n}$とするとき、$a_n$を$n$で表せ。
(3) $t_n$を求めよ。
(4) 正三角形$T_n$の面積を$S_n$とするとき、$\disp \lim_{N\to\infty}\sum_{n=1}^N S_n$ は収束するか発散するか。収束するならその値を求め、発散するならそれを示せ。
Twitterに投稿した自作問題です。
解説
(1): 正三角形$T_1$について、$\sqrt{3}t_1=\dfrac{1}{t_1}$ が成り立つから、$t_1=3^{-\frac{1}{4}}$。
(2): $t_n$と$t_{n+1}$について、
$$ t_{n+1}-t_n=\frac{1}{\sqrt{3}t_n}+\frac{1}{\sqrt{3}t_{n+1}} \quad\dou\quad t_{n+1}-\frac{1}{\sqrt{3}t_{n+1}}=t_n+\frac{1}{\sqrt{3}t_n} $$
が成り立つ。この右辺は$a_n$であり、$b_n=t_n-\frac{1}{\sqrt{3}t_n}$とすると左辺は$b_{n+1}$である。すなわち、$b_{n+1}=a_n$。一方、$a_n^2=b_n^2+\frac{4}{\sqrt{3}}$であるから、
$$ a_{n+1}^2=b_{n+1}^2+\frac{4}{\sqrt{3}} \quad\dou\quad a_{n+1}^2=a_n^2+\frac{4}{\sqrt{3}} $$
を得る。$t_1=3^{-\frac{1}{4}}$より$a_1^2=\frac{4}{\sqrt{3}}$だから、$a_n^2=\frac{4}{\sqrt{3}}n$が従う。正三角形列$\{T_n\}$の取り方から$t_n$は常に正で、したがって$a_n$も常に正だから、$a_n=2\cdot3^{-\frac{1}{4}}\sqrt{n}$。
(3): $t_n+\frac{1}{\sqrt{3}t_n}=a_n=2\cdot3^{-\frac{1}{4}}\sqrt{n}$を、$t_n$について解くと、$t_n=3^{-\frac{1}{4}}(\sqrt{n}\pm\sqrt{n-1})$を得る。正三角形列$\{T_n\}$の取り方から$t_{n+1}>t_n$であるから、複合は正が適する。したがって、$t_n=3^{-\frac{1}{4}}(\sqrt{n}+\sqrt{n-1})$。
(4): $T_n$の一辺の長さは$\frac{2}{\sqrt{3}}t_n$だから、
\begin{aligned} S_n&=\frac{\sqrt{3}}{4}\left(\frac{2}{\sqrt{3}}t_n\right)^2=\frac{1}{3}(\sqrt{n}+\sqrt{n-1})^2=\frac{1}{3}(2n-1+2\sqrt{n(n-1)}) \\ &\ge\frac{1}{3}(2n-1+2(n-1))=\frac{1}{3}(4n-3) \end{aligned}
ここで、
$$ \sum_{n=1}^N \frac{1}{3}(4n-3)=N(2N-1) \to \infty $$
だから、題意の無限和は発散する。
ネタバレ含むコメント
$x$軸とグラフの間に図形を埋めたい、というところから始まり、$\disp \int_1^\infty\!\frac{1}{x} \,dx$や調和級数は発散するけれど図形の面積和はどうなるか、という疑問から生まれました。
正方形や円を埋めてみようとしましたが、$t_n$に相当するものを解くことに難儀しました。およその議論では円や正方形の面積無限和も発散するようです。正三角形より"密に"埋めることができるので直観とも反しません。
参考文献
投稿日:2021年4月15日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中
