【東京大学2021年度入試数学(理系)第1問】基本的な、だけど意外に手こずる領域問題

note.com に書いていた解答解説記事をこちらに移植しようと思います．この問題はその第一弾です．

問題

解答解説

どちらも簡単ではあります．東大でなくても出していいレベル．しかし，(2) で困る受験生が多いかもしれません．

一方の (1) は単純です．多くの受験生が解けるでしょう．

(1) の解答

$y = x^2 + ax + b$ と $y = - x^2$ の共有点の $x$ 座標は方程式 $x^2 + ax + b = -x^2$ すなわち $2x^2 + ax + b = 0$ の解である．

$f(x) = 2x^2 + ax + b$ とおくと、$\displaystyle f(x) = x^2\left(2 + \frac{a}{x} + \frac{b}{x^2}\right)\to +\infty$ ($x\to \pm\infty$ のとき) であるので，$x$ の方程式 $f(x) = 0$ の解の一方が $-1 < x < 0$ を満たし，他方が $0 < x < 1$ を満たすための必要十分条件は，$f(-1) > 0$, $f(0) < 0$, $f(1) > 0$ を満たすことである．

• $f(-1) = 2 - a + b > 0$ すなわち $b > a - 2$
• $f(0) = b < 0$
• $f(1) = 2 + a + b > 0$ すなわち $b > - a - 2$
  であるので，求める領域は図1 の斜線部分である．ただし，周囲の太線部分はすべて含まない．

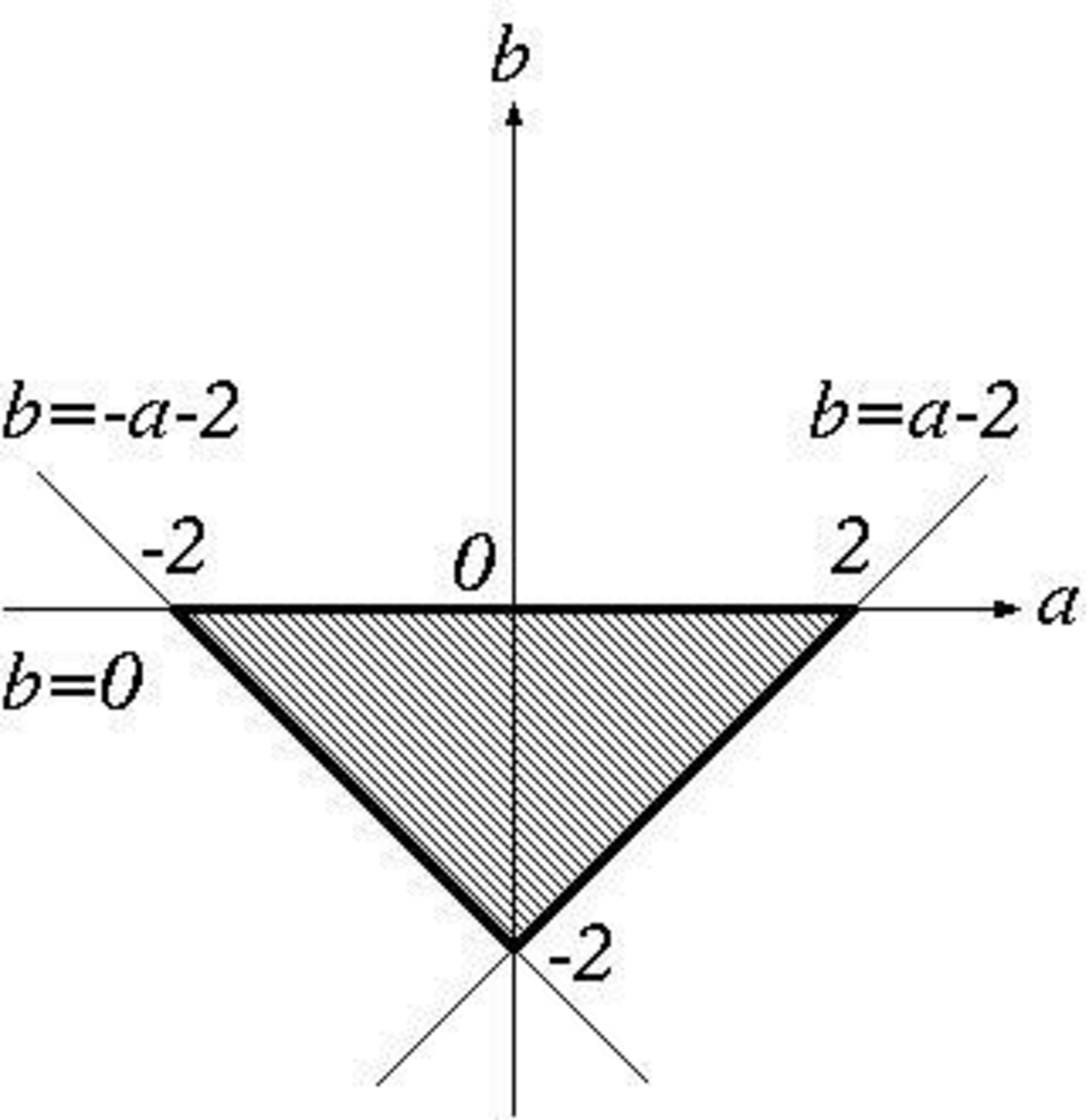(1) の答え

(2) の解答

いよいよ問題の (2) です．

何故 (1) があるかを考えると，この問題の解き方が見えてきます．実はこれがないと解くのに少々手間取った可能性があります．

そうでなくても (2) は扱いにくく感じるかもしれません．というのは，放物線 $C$ を $x$ と $y$ の方程式ではなく，$a$ と $b$ の方程式とみなします．すなわち，$b = (-x) a + y - x^2$ とみなしま．すると，この方程式は傾き $-x$，$b$ 切片 $y - x^2$ の直線となります．この直線を $l$ と呼んでおきます．

直線 $l$ が (1) の領域を通る条件を求めることで $C$ が通る領域を出していきます．それがこの問題のポイントです．

それさえ分かれば，あとは直線 $l$ の傾きで場合に分けていきます．

• $x < -1$ のとき
• $-1 \leqq x < 0$ のとき
• $0\leqq x < 1$ のとき
• $1\leqq x$ のとき

$x < -1$ のとき，直線 $l$ の傾きは $-x > 1$ であるので，直線 $l$ が (1) の領域を通るための必要十分条件は，直線 $l$ が直線 $b = 0$ と区間 $-2 < a < 2$ で交わることである．

$x < -1$ のとき

直線 $l$ に $b = 0$ を代入すると、$(-x) a + y - x^2 = 0$ となり，$x \ne 0$ から $-2 < a = \displaystyle \frac{y - x^2}{x} < 2$ が得られます．よって，$x < -1$ より $x^2 + 2x < y < x^2 - 2x$ が得られます．

$-1 \leqq x < 0$ のとき，直線 $l$ の傾きは $0 < -x \leqq 1$ であるので，直線 $l$ が (1) の領域を通るための必要十分条件は，直線 $l$ が直線 $b = -a -2$ と区間 $-2 < a < 0$ で交わることである．

$-1\leqq x < 1$ のとき

直線 $l$ に $b = -a -2$ を代入すると，$-a -2 = (-x) a + y - x^2$ すなわち $(x - 1) a = y - x^2 + 2$ となり，$x \ne 1$ から $-2 < \displaystyle\frac{y - x^2 + 2}{x-1} < 0$ が得られます．よって，$x - 1 < 0$ より $x^2 - 2 < y < x^2 - 2x$ が得られます．

$0 \leqq x < 1$ のとき，直線 $l$ の傾きは $-1 < -x \leqq 0$ であるので，直線 $l$ が (1) の領域を通るための必要十分条件は，直線 $l$ が直線 $b = a -2$ と区間 $0 < a < 2$ で交わることである．

$0\leqq x < 1$ のとき

直線 $l$ に $b = a -2$ を代入すると，$a -2 = (-x) a + y - x^2$ すなわち $(x + 1) a = y - x^2 + 2$ となり，$x \ne -1$ から $0 < \displaystyle\frac{y - x^2 + 2}{x+1} < 2$ が得られます．よって，$x + 1 > 0$ より $x^2 - 2 < y < x^2 + 2x$ が得られます．

$1 \leqq x$ のとき，直線 $l$ の傾きは $-x < -1$ であるので，直線 $l$ が (1) の領域を通るための必要十分条件は，直線 $l$ が直線 $b = 0$ と区間 $-2 < a < 2$ で交わることである．

$1\leqq x$ のとき

直線 $l$ に $b = 0$ を代入すると，$(-x) a + y - x^2 = 0$ となり，$x \ne 0$ から $-2 < a = \displaystyle\frac{y - x^2}{x} < 2$ が得られます．よって，$x \geqq 1$ より $x^2 - 2x < y < x^2 + 2x$ が得られます．

以上を合わせると次の領域となります：図6 において，各区間で3つの放物線のうちの一番下の放物線から一番上の放物線に挟まれる領域で，境界線(放物線上)を含みません．

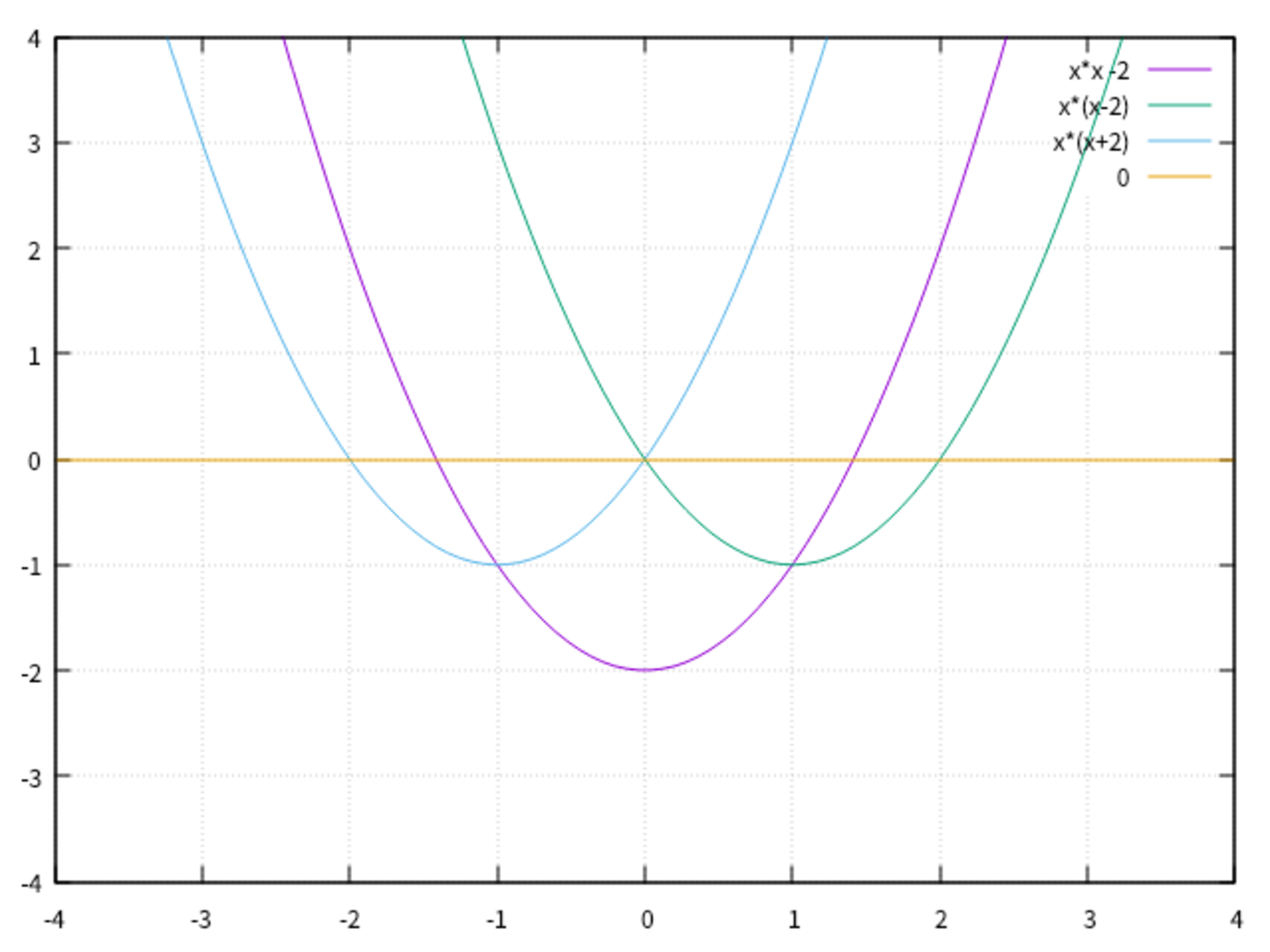(2) の答え

感想

問題そのものはそれほど難しくないのですが，(2) で放物線 $C$ を $a$ と $b$ の直線の方程式としてみなすことが出来るかどうかがカギです．

学生時代に同級生に数学を教えたことは何度もあるのですが，その経験から言うと，こういう変数と定数の切り替えが案外できないもので，最初に $x$, $y$ は変数, $a$, $b$ は定数と考えてしまうと，そこから抜け出せなくなります．

しかしながら，この問題のように場面場面で変数と定数の役割を入れ替えることはよくあります．そこを意識することが重要．そういう意味で，最初から地味にいやらしい点を突いてきたなという印象です．(決して悪い意味ではありません．)