大学数学基礎解説

【東京大学2021年度入試数学(理系)第2問】複素数＝ベクトル、ってだけの問題

大学入試,複素数平面

218

今年の東大(理科)の第2問は複素数平面の問題ですが，易しい問題です．というより，しょーもない問題です．

問題

複素数 $a$, $b$, $c$ に対して整式 $f(z) = az^2 + bz + c$ を考える．$i$ を虚数単位とする．

$\alpha$, $\beta$, $\gamma$ を複素数とする．$f(0) = \alpha$, $f(1) = \beta$, $f(i) = \gamma$ が成り立つとき，$a$, $b$, $c$ をそれぞれ $\alpha$, $\beta$, $\gamma$ で表せ．
$f(0)$, $f(1)$, $f(i)$ がいずれも $1$ 以上 $2$ 以下の実数であるとき，$f(2)$ のとりうる範囲を複素数平面上に図示せよ．

解答解説

そもそも複素関数って範囲なのか？という疑問はあるのですが，微分しているわけではないので，このくらいはいいでしょう．

複素関数

高校の学習指導要領では実数係数＋実数定義域からなる関数(実数関数)までしか認められていなかったと記憶しています．複素数係数＋複素数定義域からなる関数(複素関数)は許されていないはずなので，厳密なことを言えばこの問題は学習指導要領の範囲から外れています．

個人的には，この程度のことであれば問題ないと思いますが．

(1) の解答

実際に $f(0)$, $f(1)$, $f(i)$ を求めてみましょう．

$f(0) = c = \alpha$
$f(1) = a + b + c = \beta$
$f(i) = -a + bi + c = \gamma$

$c$ はすでに出ているので，あとは $a$ と $b$ のみです．$f(1)+f(i)=(1 + i) b + 2c = \beta + \gamma$ より
\begin{equation} b = \displaystyle\frac{\beta + \gamma - 2\alpha}{1 + i} = \frac{(1 - i)(\beta + \gamma - 2\alpha)}{2} \end{equation}
$f(1) + if(i) = (1 - i) a + (1 + i) c = \beta + \gamma i$ より
\begin{equation} a = \displaystyle\frac{β + γi - (1 + i)α}{1 - i} = \frac{(1 + i)\{β + γi - (1 + i)α\}}{2} \end{equation}

$a$ と $b$ のまとめ方はどうでもいいでしょう．答えにいろんな書き方があって，地味に採点が大変そうだと思うのは私だけでしょうか？

(2) の解答

$f(2)$ を $\alpha$, $\beta$, $\gamma$ の式で表せばほぼ終わりです．
\begin{align} f(2) &= 4a + 2b + c\\ &= 2(1 + i)\{\beta + \gamma i -(1 + i)\alpha\} + (1 - i)(\beta + \gamma - 2\alpha) + \alpha\\ &= (3 + i)\beta + (-1 + i)\gamma + (-1 -2i)\alpha\\ &= 1 + (3 + i)(\beta - 1) + (-1 + i)(\gamma - 1) + (-1 -2i)(\alpha - 1) \end{align}
ここで、$1 \leqq \alpha, \beta, \gamma \leqq 2$ すなわち $0 \leqq \alpha -1, \beta -1, \gamma -1 \leqq 1$ であることから，次の斜線部分が答えとなります．

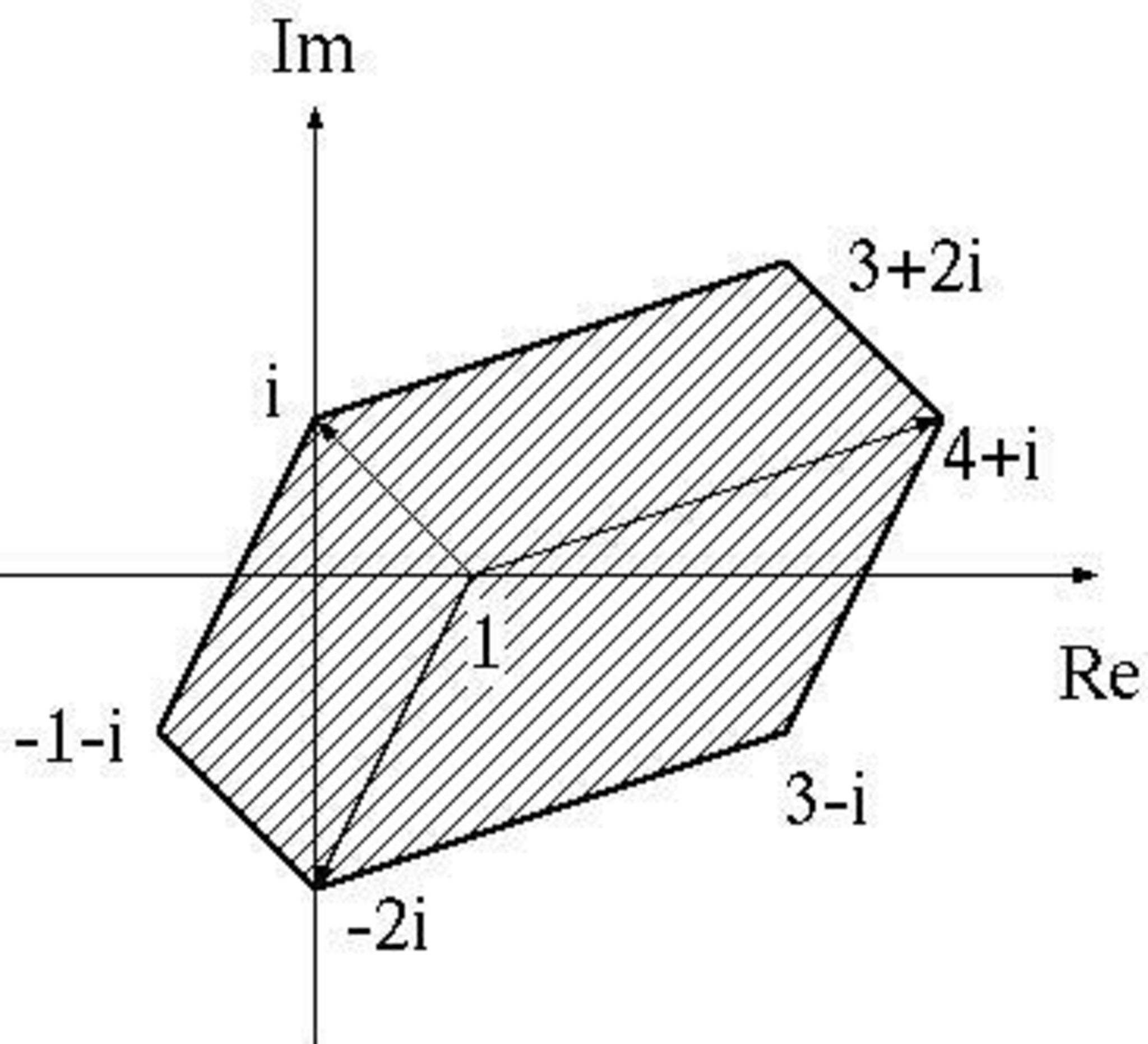(2) の答え

要するに、$3 + i$, $-1 + i$, $-1 -2i$ の3つの複素数から 2つを取り出して，原点，2つの複素数，2つの複素数の和を頂点とする平行四辺形を $+1$ 方向に平行移動します．この図形を $D$ とします．

このとき，残る 1つの複素数の方向に $D$ を平行移動したときの $D$ が通過する領域が求める領域となります．

例えば、$3 + i$ と $-1 + i$ を取り出したとすると，$0$, $3 + i$, $2 + 2i$, $-1 + i$ を頂点とする平行四辺形を $+1$ 方向に平行移動すると，$1$, $4 + i$, $3 + 2i$, $i$ を頂点とする平行四辺形ができます．これが $D$ です．