【京都大学2021年度前期入試数学(理系)第6問】全く趣の異なる2問組

東大の入試を取り上げている最中ですが，京大の第6問が面白かったのでアップしました．問題が2つありますが，全く関連がありません．何故このような組み合わせになったのか不思議です．

(上記は note.com にアップしていたときの状況です．)

問題

解答解説

問1 の解答

この問題は背理法で簡単に導けます．

$n$ が素数でないと仮定すると $2$ 以上の整数 $p$, $q$ を用いて $n = pq$ と表すことが出来る．このとき，
\begin{equation} 　　　3^n - 2^n = (3^p - 2^p)(3^{p(q-1)} + 3^{p(q-2)}2^p + 3^{p(q-3)}2^{2p} + … + 2^{p(q-1)}) \end{equation}
と因数分解できる．$p$, $q$ が $2$ 以上の整数であることから，$3^p-2^p$ は整数で，$3^p - 2^p=2^p\displaystyle\left\{\left(\frac{3}{2}\right)^{p}-1\right\}\geqq 4\times\displaystyle\frac{5}{4}=5$ であり，$3^{p(q-1)} + 3^{p(q-2)}2^p + 3^{p(q-3)}2^{2p} + … + 2^{p(q-1)}$ も整数で，$3^{p(q-1)} + 3^{p(q-2)}2^p + 3^{p(q-3)}2^{2p} + … + 2^{p(q-1)}\ge 3^{p(q-1)}+2^{p(q-1)}\ge 3^2+2^2=13$であるので，$3^n - 2^n$ は合成数であり，素数ではない．

よって，$3^n - 2^n$ が素数ならば $n$ も素数である．

問2 の解答

この問題は，解く前にいろいろと図を描いて情報を集めるとわかりやすいと思います．

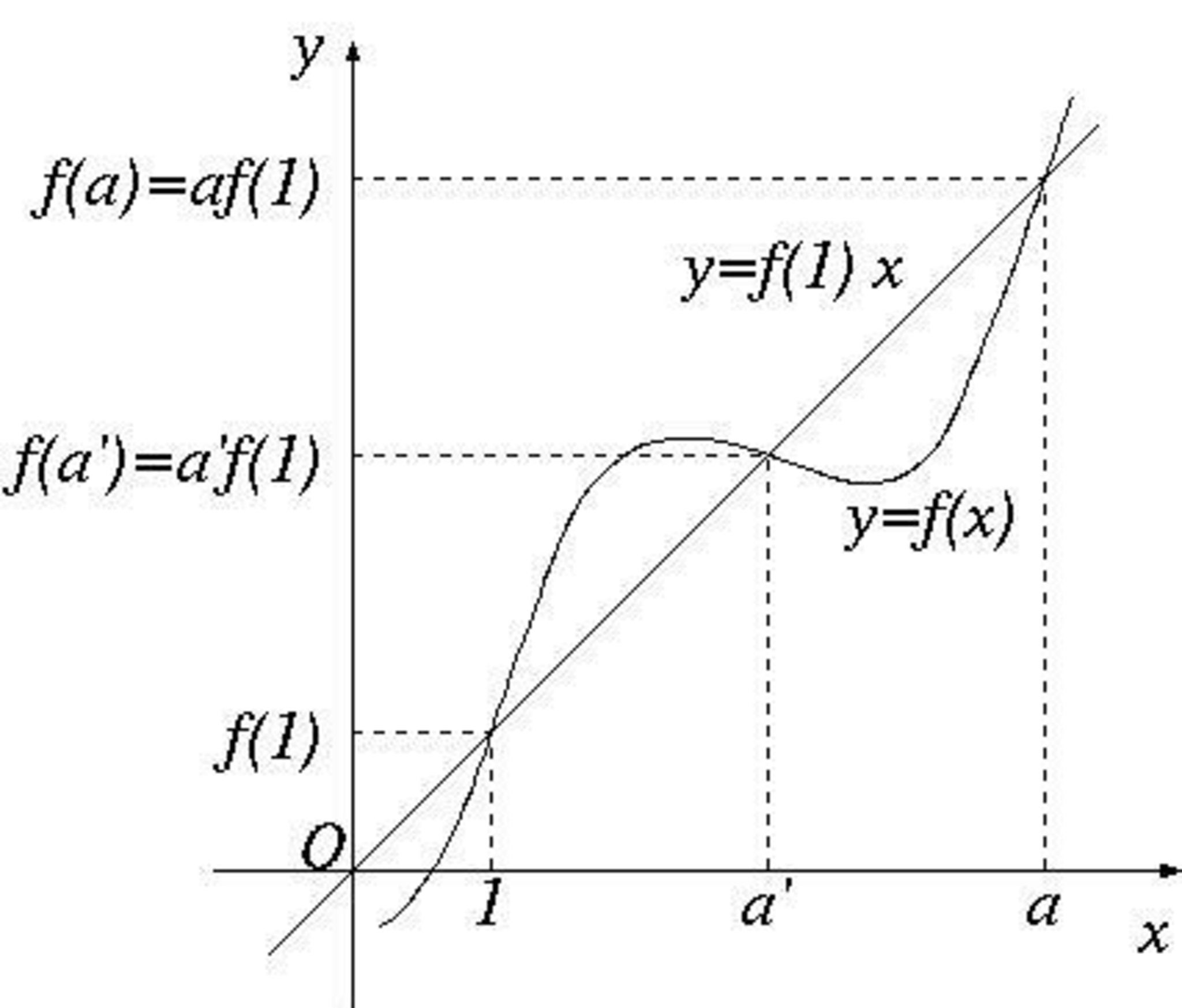第6問　問2の状況

条件から 2点$(1, f(1))$ と $(a, f(a))=(a,af(1))$ を通る直線の方程式は $y = f(1) x$ となるため原点を通ります．したがって，$f'(1) = f(1)$ もしくは $f'(a) = f(1)$ となる場合には条件を満たします．

ということで，議論となるのは$f'(1) \ne f(1)$ かつ $f'(a) \ne f(1)$ のときにどうなるかです．

仮に $x = c$ における $y = f(x)$ の接線が原点を通るとすると，$(x, y) = (0, 0)$ が接線の方程式 $y = f'(c)(x - c) + f(c)$ を満たすので，$f(c) = c f'(c)$ が成立することになります．逆に，$f(c) = c f'(c)$ を満たす $c$ が存在すれば，$x = c$ における $y = f(x)$ の接線が原点を通ります．

このことを踏まえて，$g(x) = f(x) - x f'(x)$ とおきます．上記の通り，$g(c) = 0$ である $c$ が存在すれば証明終了です．

さらに，$h(x) = f(x) - x f(1)$ とおきます．このとき，$f(1)=f(a)=0$ となります．これがなぜ出てきたかはのちほど分かると思います．

一般性を失うことなく $f'(1) > f(1)$ と仮定します．このとき，非常に小さい $\varepsilon > 0$ に対して $\displaystyle\frac{ f(1+\varepsilon) - f(1) }{\varepsilon} > f(1)$ となり，$f(1+\varepsilon) > f(1) + \varepsilon f(1) = (1+\varepsilon)f(1)$ であるので，$h(1+\varepsilon) > 0$ となります．

$f'(a) > f(1)$ と仮定します．このとき，非常に小さい $\varepsilon > 0$ に対して $\displaystyle\frac{ f(a-\varepsilon) - f(a) }{-\varepsilon} > f(1)$ となり，$f(a-\varepsilon) < f(a) - \varepsilon f(1) = a f(1) - \varepsilon f(1) = (a-\varepsilon) f(1)$ であるので，$h(a-\varepsilon) < 0$ となります．

よって，中間値の定理より $h(a') = f(a') - a' f(1) = 0$ すなわち $f(a') = a' f(1)$ となる $1 < a' < a$ が存在するので，$a'$ を新たな $a$ とします．(ちょうど図1 のグラフの状況です．)

これを繰り返すことにより，$f'(a) < f(1)$ と仮定して一般性を失いません．このとき，$g(1) = f(1) - f'(1) < 0$ かつ $g(a) = f(a) - a f'(a) > a f(1) - a f(1) = 0$ であるので，中間値の定理より $g(c) = 0$ である $1 \leqq c \leqq a$ が存在します．

$f'(1) < f(1)$ のときも同様に $g(c) = 0$ である $1 \leqq c \leqq a$ が存在します．

よって，$x = c$ における $y = f(x)$ の接線が原点を通ります．

感想

問1 はしょうもないですが，問2 は面白いです．おそらく，どのように手を出していいかが悩ましかったのではないでしょうか？

いきなり関数 $g$ を導入すると訳が分からないと思い，$g$ の意図を述べてから証明を書きましたが，実際に答案を書くときには必要ないでしょう．

まず $g(x)$ を導入して，$g(c) = 0$ を満たす $c$ に対して $x = c$ における $y = f(x)$ の接線が原点を通ることを示し，実際に $g(c) = 0$ を満たす $c$ が存在することを証明して終わります．

ここで巧妙なのは $a$ のとり方です．関数 $h$ のとり方，と言ってもいいです．この部分は実際にグラフを描いてみないとわかりにくいと思います．

$f'(1) > f(1)$ のとき，$f'(a) < f(1)$ であれば $x = 1$ での接線の $y$ 切片は負，$x = a$ での接線の $y$ 切片は正になるので，途中に原点を通る接線があることが分かるのですが，$f'(a) > f(1)$ の場合に $x = a$ での接線の $y$ 切片も負になるため，困ったことが起こってしまいます．

このとき，$x = 1$ の直後に $y = f(x)$ が $y = f(1) x$ より上にあり，$x = a$ の直前では $y = f(x)$ が $y = f(1) x$ より下にあるので，$x = 1$ と $x = a$ の間で $y = f(x)$ と $y = f(1) x$ が交わることを意味します．

この，$y = f(1) x$ より上か下かを表しているのが $h$ という関数です．

もう少し突っ込んだ話をすると，$f(a) = a f(1)$ となる最小の $a > 1$ が存在すればよかったのですが，最小の $a$ が存在する保証がないため，代わりに関数 $h$ を導入しています．

もし最小の $a$ が存在したとすると次のどちらかが成立します：

• 任意の $x$, $1 < x < a$, に対して $f(x) > x f(1)$
• 任意の $x$, $1 < x < a$, に対して $f(x) < x f(1)$

したがって，次のどちらかが成立します：

• $f'(1) > f(1)$ かつ $f'(a) < f(1)$
• $f'(1) < f(1)$ かつ $f'(a) > f(1)$

例えば，任意の $x$, $1 < x < a$, に対して $f(x) > x f(1)$ であるならば，非常に小さい $\varepsilon > 0$ に対して $\displaystyle\frac{ f(1+\varepsilon) - f(1) }{\varepsilon} > \frac{ (1+ε) f(1) - f(1) }{\varepsilon} = f(1)$ かつ $f'(1) \ne f(1)$ であることから $f'(1) > f(1)$ が成立し，$\displaystyle\frac{ f(a-ε) - f(a) }{-\varepsilon} < \frac{ (a-ε)f(1) - a f(1) }{\varepsilon} = f(1)$ かつ $f'(a) \ne f(1)$ であることから $f'(a) < f(1)$ が成り立ちます．

しかし，この証明方法では減点は免れないかもしれません．減点覚悟で書く分には悪くないと思いますが．

某予備校や某雑誌の解答では，$F(x)=\displaystyle\frac{f(x)}{x}$ とおいて，
\begin{equation} 　　　F(a)=\frac{f(a)}{a}=\frac{af(1)}{a}=f(1)=F(1) \end{equation}
かつ
\begin{equation} 　　　F'(x)=\frac{f(x)-xf'(x)}{x^2} \end{equation}
から
\begin{equation} 　　　\frac{F(a)-F(1)}{a-1}=F'(c)\ すなわち\ \frac{f(c)-cf'(c)}{c^2}=0\ すなわち\ f(c)=cf'(c) \end{equation}
をみたす $1< c< a$ が存在することを示しています．この証明は非常にきれいでいうことはないのですが，実戦で $F(x)$ を思いつくかは疑問です．一般の受験生には難しい気がします．

今回提示させていただいているのは初見での解答で，実戦的だと思っています．そのため，その場で何を考えているかが分かるように関数 $g$ と $h$ の意図も書いたつもりです．

この問題は間違いなく難問の部類ですが，決して解くのが不可能な問題でもありません．条件を整理する能力が問われていますので，普段からこういう問題に慣れておくといいでしょう．