京大2006文系第５問を帰納法で解く
今回のテーマは、京大2006文系第５問を帰納法で解く、です。
$n,k$は自然数で$k\leq n$とする。穴のあいた$2k$個の白玉と$2n-2k$個の黒玉に紐を通して輪を作る。このとき適当な二箇所で紐を切って$n$個ずつの2組にわけ、どちらの組も白玉$k$個、黒玉$n-k$個からなるようにできることを示せ。
受験生の中では割と有名問題なので、ご存知の方も多いと思います。先に答えを言ってしまうと、輪を半分にする境界をカチカチ回転させて、その片側の白玉、黒玉の個数の推移を追うことで、中間値の定理もどきが使えて解決します。しかし、今回は別の方法を考えたいと思います。というのも、多くの参考書や解説記事では、「帰納法を使ってみようと思うのも悪くはないが、残念なことにこの問題ではうまく行かない」などと、帰納法によるアプローチが断念されていました。だったら帰納法でやってやろうじゃないかと(笑)。なかなか味わいのある解法になったと思いますのでぜひ読んでみてください！
$n=k$のとき題意は自明だから$n>k$で考える。したがって$n\geq2$とする。
$n$に対して、$n$未満の任意の自然数$k$について題意が成り立つことを$P(n)$とする。$n$についての帰納法で示す。
(i)$n=2$のとき
$k=1$より、白玉2個と黒玉2個なので、時計回りに「白黒白黒」か「白白黒黒」のどちらかで、前者はどこで切っても題意をみたし、後者は白と白の間で切ればよいから、$P(2)$は成り立つ。
(ii)$P(2),\cdots ,P(n-1)$が成り立つと仮定する。$P(n)$を考える。
下図のように、連続した$n$個を考える。
連続n個
この中の白玉の個数は$0$以上$2k$以下の$2k+1$通りで、一方このような$n$個の選び方は$2n$通りである。いま、$n>k$より$2n>2k+1$であるから、鳩の巣原理より含む白玉の個数が等しい$2$つの連続$n$個の選び方が存在する。それらの位置関係で場合わけする。
(a)それらが重ならないとき
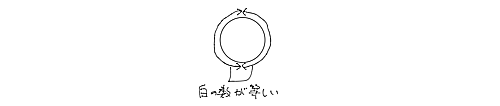2つの連続n個が重ならない
これはすでに題意を満たしている。(白玉と黒玉を同数ずつに分けられている。)
(b)それらが重なるとき
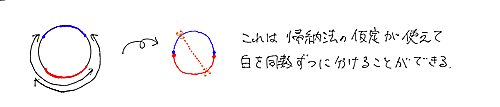2つの連続n個が重なる
上図のように重なり(赤)と円の中心に関してそれと対称な部分(青)をくっつけて新たな円とすると、これは白玉と黒玉が偶数個ずつで総数が$2n$個未満であるから、帰納法の仮定が使えて白玉を(したがって黒玉も)同数ずつに切り分けることができる。そしてその切り方は、元の円においても題意を満たすものであり、$P(n)$が成り立つ。
以上より$P(n)$は任意の自然数$n$で成り立つ。[証明終]
いかがだったでしょうか。鳩の巣原理がうまく効いていて、お気に入りの解法です。
読んでいただきありがとうございました。
この記事を高評価した人
この記事に送られたバッジ
投稿者
