好きな極限の公式

　黒狐です。初めて投稿させていただきます。何をやったらいいのかいまいちピンとこないので、とりあえず自分が個人的に好きな極限の公式を証明するのとかやってみようかなと思います。
　次の公式になります。センタリングどうやるんだろ・・$$ \lim_{x\to 0}\frac{\tan(\sin(x)) - \sin(\tan(x))}{x^7} = \frac{1}{30}. $$なるほど、普通にドルマーク2つで囲うとセンタリングになるんですね・・
　証明は綺麗なものがあるわけではなく、展開して比べるだけです（地味です）。
　最初は馬鹿正直にそれぞれ$\sin$と$\tan$のテーラー展開に従ってそれらの累乗を作って差を取って比較、という風にやろうとしたのですが計算ミスしやすいので別の手段に頼ることにしたのは何となく覚えています（かなり昔に取り組んだのでうろ覚え）。$$ \tan(x) = \frac{\sin(x)}{\sqrt{1 - {\sin}^2 x}} $$ですから、$z=\sin x$と変数変換して、$$ \mbox{求める極限}~ = ~ \lim_{z \to 0}\frac{1}{(\arcsin z)^7}\cdot \left( \tan z - \sin \frac{z}{\sqrt{1 - z^2}} \right) $$ とすると多少楽になります。
　$z^7$を使って逆三角関数の部分を消すと、
$$ \mbox{求める極限} ~=~ \lim_{z \to 0}\frac{z^7}{(\arcsin z)^7} \cdot \frac{1}{z^7} \left( \tan z - \sin \frac{z}{\sqrt{1 - z^2}} \right)$$
となりますが、
$$ \lim_{z \to 0}\frac{z}{\arcsin z} = \lim_{x \to 0}\frac{\sin x}{x} = 1 $$
なのでドットの前は1で、ドットの後ろが問題になります。ここは、このままだと分数が問題になるので、
$$ \lim_{z \to 0}\frac{1}{(\sqrt{1 - z^2})^7}\cdot\frac{1}{z^7}\cdot \left( (\sqrt{1 - z^2})^7 \cdot \tan z - (\sqrt{1 - z^2})^7 \sin \frac{z}{\sqrt{1 - z^2}} \right) $$ と変形します。そして括弧の中の2項をそれぞれテーラー展開して比較します。
　まず、一般二項定理より、
$$ (1 - a)^m = 1 - ma + \frac{m(m-1)}{2}a^2 - \frac{m(m-1)(m-2)}{6}a^3 + \cdots $$ ですから、
$$ (\sqrt{1 - z^2})^7 = (1 - z^2)^{7/2} = 1 - \frac{7}{2}z^2 + \frac{35}{8}z^4 - \frac{35}{16}z^6 + o(z^7) $$ となります。ちなみにこれはランダウ記号で、
$$ \lim_{t \to 0}\frac{o(t^7)}{t^7} = 0 $$ というような意味です。項の一部がこれを満たすような場合にまとめてこう書いてしまおうというわけで、この性質しか用いない場合に多用される書き方です（この性質以外の情報は捨てるということ）。
　次に、タンジェントの微分が、
$$ \frac{d^k}{dz^k} \tan z |_{z=0} = 0,~ 1,~ 0,~ 2,~ 0,~ 6,~ 0,~ 272,~\cdots ~~(k=0,~1,~2,~\cdots) $$ ですから、テーラー展開で、
$$ \tan z = z + \frac{2}{6}z^3 + \frac{16}{120}z^5 + \frac{272}{5040}z^7 + o(z^7) $$ で、約分して、
$$ \tan z = z + \frac{1}{3}z^3 + \frac{2}{15}z^5 + \frac{17}{315}z^7 + o(z^7) $$ となります。2つを掛けると、
$$ \frac{1}{16}(16-56z^2+70z^4-35z^6)\cdot \frac{1}{315}(315z+105z^3+42z^5+17z^7) + o(z^7) $$ となります。これを間違えずに計算して、
$$ (\sqrt{1 - z^2})^7 \tan z = \frac{1}{5040}(5040z - 15960z^3 + 16842z^5 - 5755z^7) + o(z^7) $$ を得ます。
　次に、もう一つの方は、$\sin t$のテーラー展開：
$$ \sin t = t - \frac{1}{6}t^3 + \frac{1}{120}t^5 - \frac{1}{5040}t^7 + o(t^7) $$ を使うと、平方根がうまい具合に消えて、
$$ (\sqrt{1 - z^2})^7 \cdot \sin\frac{z}{\sqrt{1 - z^2}} $$ が、
$$ z(1-z^2)^3 - \frac{z^3(1-z^2)^2}{6} + \frac{z^5(1-z^2)}{120} + \frac{z^7}{5040} + o(z^7) $$
となります。これはさっきほどは難しくないかもです・・間違えずに計算すると、
$$ (\sqrt{1 - z^2})^7 \cdot \sin\frac{z}{\sqrt{1 - z^2}} = \frac{1}{5040}(5040z - 15960z^3 + 16842z^5 - 5923z^7) + o(z^7) $$ となります。このようにほぼ同じような感じになります。
　一つ目から二つ目を引くと、
$$ \frac{1}{z^7}(\mbox{ひとつめ} - \mbox{ふたつめ}) = \frac{1}{5040z^7}(-5755z^7 - (-5923)z^7 + o(z^7)) = \frac{168}{5040} + o(1) = \frac{1}{30} + o(1). $$
これで証明できたのですが、本質がつかめなかったので、何かいい証明方法がないかなと未だに疑問に思ってます。
　ピンとこないと思うのでInigo Quilezさんの（これすごく便利なのですが） Graphtoy というサービスでグラフを描いてみたので貼り付けておきます。オレンジが$\tan(\sin(x))$で青が$\sin(\tan(x))$です。0の近くで綺麗に重なっています。
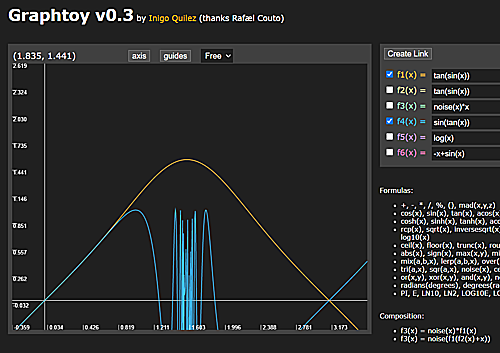tan(sin(x))とsin(tan(x))の比較