特異曲線とその正規化を用いた特異点解消
導入
$k$を体とする．$k[x,y] \to k[t^2, t^3]$の Ker を求めよ．
解説
$k$を(代数閉)体とします．この時，$k[x,y] \to k[t^2, t^3]$はより正確に書くと
$$
\begin{array}{cccc}
\phi: & k[x,y] & \to & k[t] \\
& f(x,y) & \mapsto & f(t^2, t^3)
\end{array}
$$
という意味です．
これはつまり，$k$係数の2変数多項式の$x$に$t^2$を代入し，$y$に$t^3$を代入することによって1変数の多項式に変換する写像です．これは代入写像なので準同型写像になります．よってその核(Ker)は$k[x,y]$のイデアルになります．
準同型写像とは簡単に言うと構造を保つ写像のことで，今の場合環$A,B$に対して$f: A\to B$が環の準同型写像であるとは，
- $f(0_A) = 0_B$
- $f(a + b) = f(a) + f(b)$
- $f(ab) = f(a)f(b)$
が成り立つことをいいます．つまり，足し算掛け算してから写像で写したものと，写してから足し算掛け算したものが同じになる，という意味です．また準同型の核$\Ker$とは
$$
\Ker f = \{a \in A \mid f(a) = 0\}
$$
と定義されます．つまり，$f$で写すと$B$の中で$0$になってしまうもののことです．
線形写像やその核（や像）といった言葉は大学の線形代数などで聞き馴染みのあるかもしれませんが，環の準同型やその核はそれらの類似および拡張された概念です．
さて，どのようなものが核に含まれるでしょうか？一番簡単なものは$f = x^3 - y^2$ですね．実際
\begin{align}
\phi(f) &= (t^2)^3 - (t^3)^2 \\
& = t^6 - t^6 = 0
\end{align}
となるので$f \in \Ker\phi$となります．他にも，$g = x^4 + x^3y - xy^2 - y^3$なども核に含まれます．
\begin{align}
\phi(g) &= (t^2)^4 + (t^2)^3t^3 - t^2(t^3)^2 - (t^3)^3 \\
& = t^8 + t^9 - t^8 - t^9 = 0
\end{align}
$k[x,y]$はネーター環なので(ヒルベルトの基底定理)，そのイデアルは有限個の元で生成されます．つまり，有限個の元をいくつか選んでくれば核になるわけです．
ここで，実は$g = (x^3 - y^2)(x + y)$となっており，$g \in (f)$でした．この発想から$\Ker \phi = (f) = (x^3 - y^2)$なのではないかと予想を立ててこれを証明してみたいと思います．
$$\Ker \phi = (x^3 - y^2)$$
明らかに$\Ker \phi \supseteq (x^3 - y^2)$が成り立つ（上で確認した）．以下では$\Ker \phi \subseteq (x^3 - y^2)$を示す．つまり，任意の$g\ \in \Ker$に対して$g \in (x^3 - y^2)$であることを示す．
$g \in k[x,y]$は一般的に$a_{ij}\in k$を用いて$g = \sum a_{ij}x^i y^j$と表される．この$g$を$f$で剰余すると，
$$
g = g_0(x) + g_1(x)y + (f)
$$
となる．これは$g$の中で$y$に注目し，$y$の指数が0と1の時をまとめ，それぞれ$x$の多項式になっている部分を$g_0, g_1 \in k[x]$と置いたものである．$y$の指数が2以上であるとき，イデアル$(f)$で剰余する，つまり
$$
x^3 - y^2 = 0
$$
という関係式で変数のリダクションを行うので，$x$の式に置き換わる．例えば$xy^3$という単項式は
\begin{align}
xy^3 &= x(y^2)y\\
&= x(x^3)y + (f) \\
&= x^4y + (f)
\end{align}
と計算され，上記の$g$の表現における$g_1(x)y$の部分に入る．このようにして$y$の指数が2以上である単項式は全てイデアル$(f)$で割ったあまりの部分に入る．
さて$g \in \Ker \phi$と仮定すると，
\begin{align}
\phi(g) &= \phi(g_0(x) + g_1(x)y + (f)) \\
&= \phi(g_0(x) + g_1(x)y) \quad (\because f \in \Ker\phi)\\
&= g_0(t^2) + g_1(t^2)t^3 = 0
\end{align}
となる．ここで，$g_0(t^2)$の部分は$t$の指数が全て偶数であり，$g_1(t^2)t^3$の部分は$t$の指数が全て奇数となる．つまり，同じ単項式は$g_0(t^2)$と$g_1(t^2)t^3$の部分で出てこないので，$\phi(g) = 0$ならば$g_0 = g_1 = 0$でなければならない．よって$g \in (f)$となる．$\square$
以上で命題を示すことができました．
特異点
さて，このようにして求めた$\Ker$について，代数幾何学の視点から考えてみたいと思います．
$\psi: \mathbb{A}^1 \to \mathbb{A}^2$を$\psi(t) = (t^2, t^3)$とします．この時$\Im \psi \subset \aa^2$をプロットすると
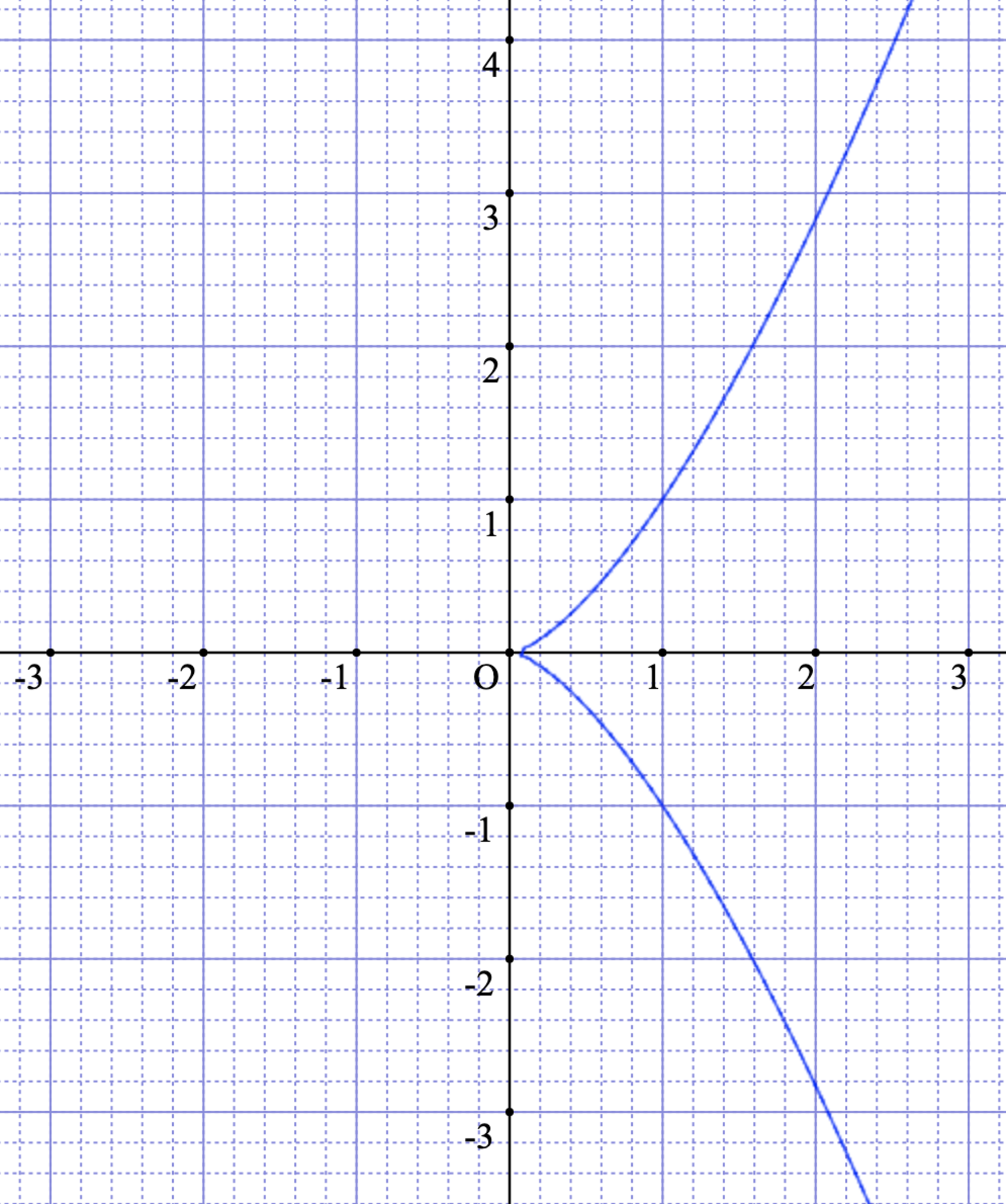cuspidal curve
となります．$k$上のアフィン多様体の間の射は$k$代数の準同型を誘導しますが，ちょうど$\psi$が誘導する$k$代数準同型が$\phi$になっています．このとき
$$
k[\Im\psi] = \Im\phi \simeq k[x,y] / \Ker\phi
$$
という対応関係から$\Im\psi = V(\Ker\phi) = V(x^3 - y^2)$となり，これはつまり$x^3 - y^2 = 0$という曲線を表しています．要するに，今までやってきたことは$\psi$がなす軌跡を定義する方程式を求めていたことになります．
さらに，原点付近を見てもらえれば分かる通り，この曲線は原点において尖った形をしています．このような点を尖点(cusp)と言います(詳細な定義は割愛[2])．
この曲線は尖点以外の点では接線が一つに定まります．例えば$P = (1,1)$では
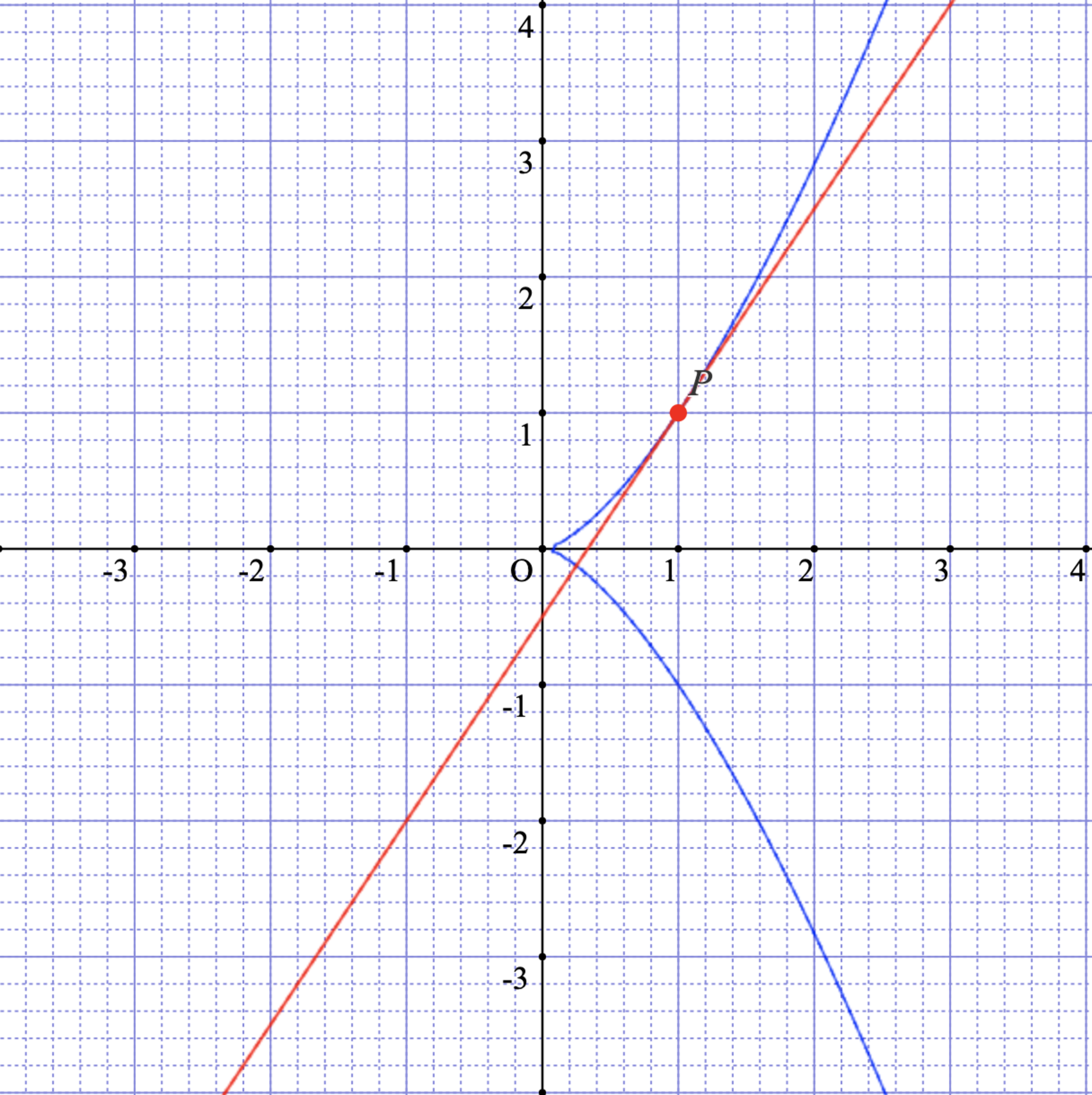(1,1)での接線
赤色の線を接線として1つ得ることができます．しかし，原点では接線が2重になった形で出てきてしまいます．
(0,0)での接線
「おい，基底．どう見ても1本じゃねえかタコすけぇ！」と言われてしまうかもしれませんが，上からくる接線と下からくる接線がだんだんと原点に近づく様子を考えると，ちょうど原点で2本重なっている気持ちを分かってもらえると思います．
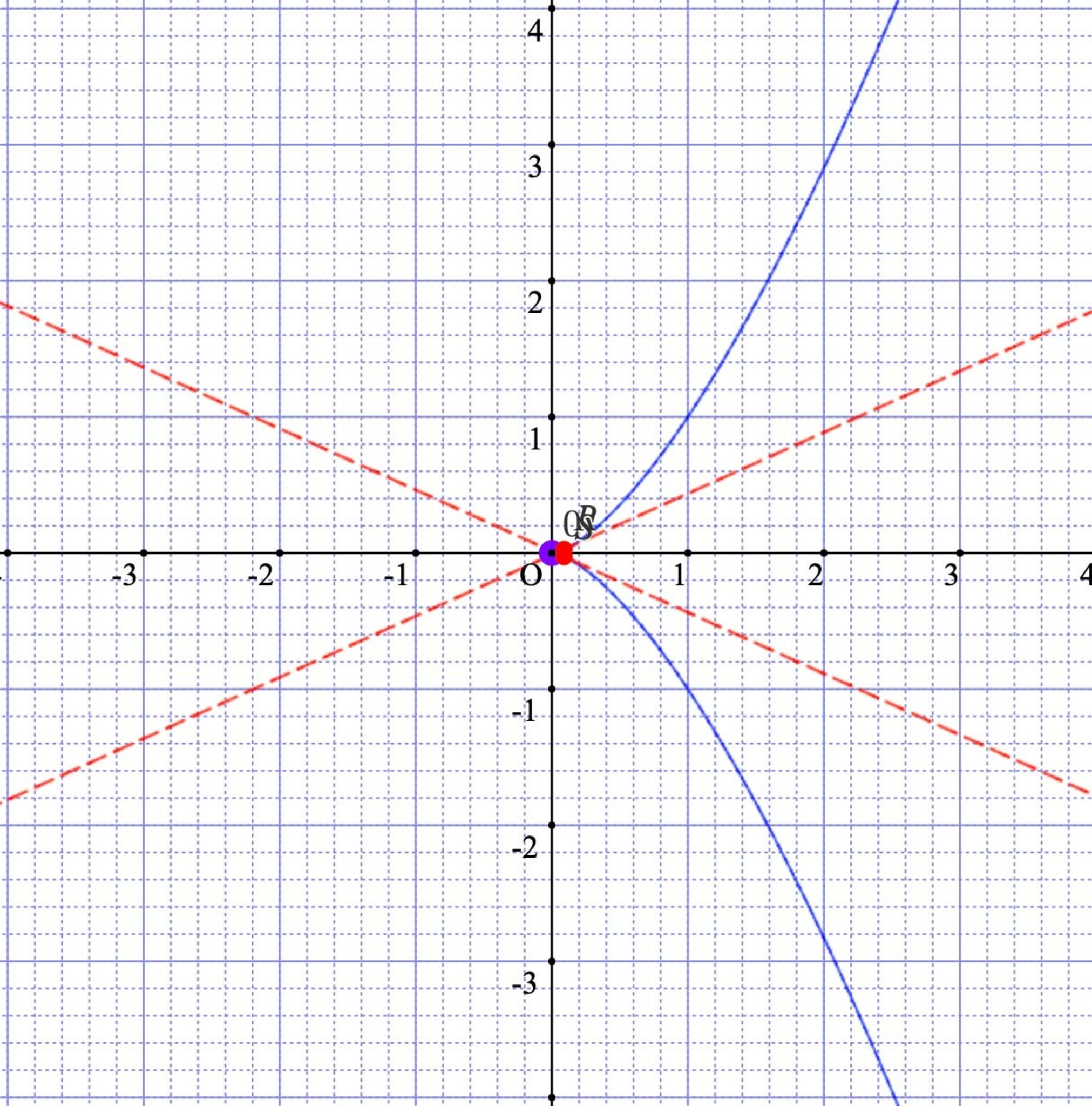
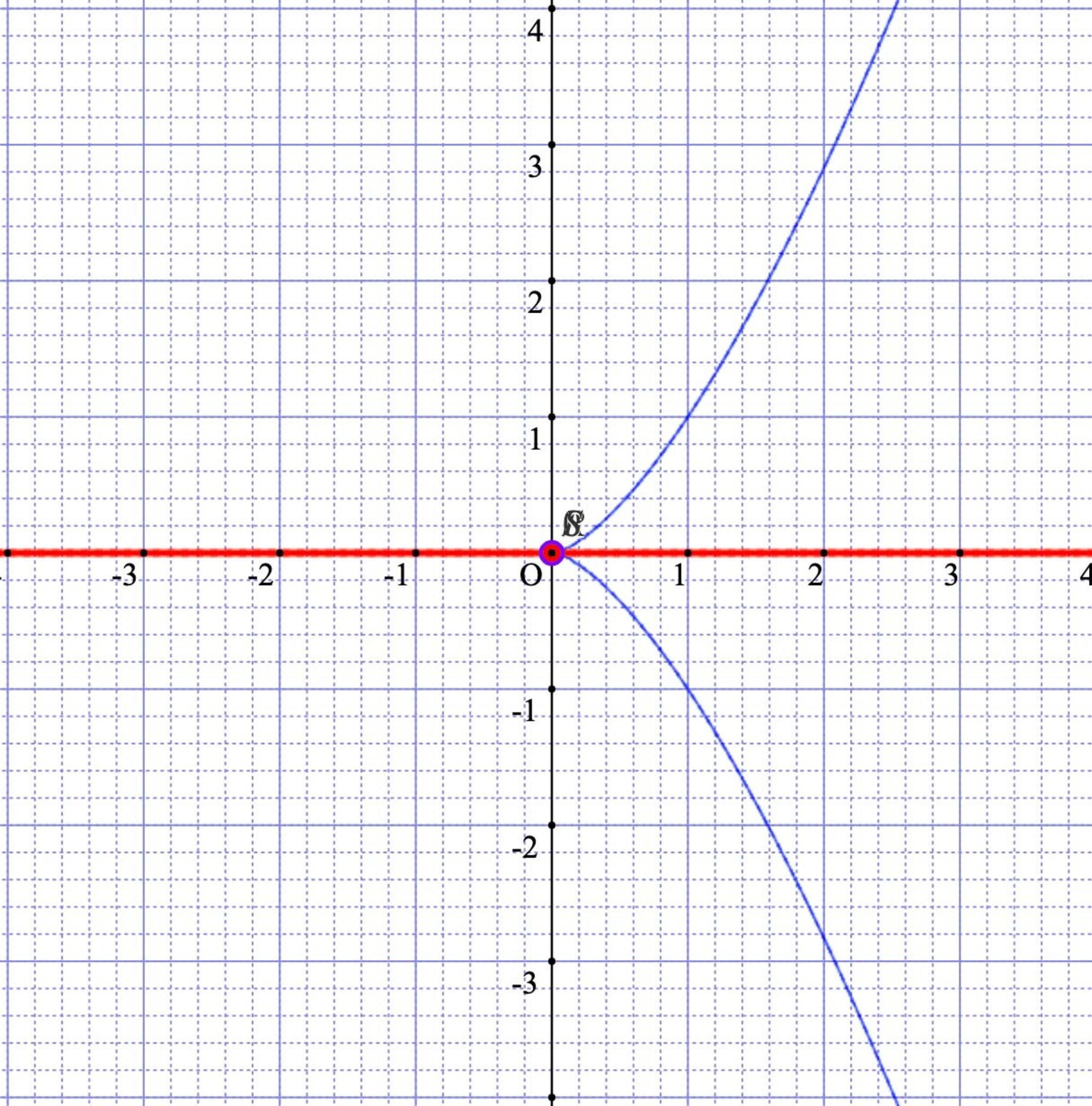
このように，接線が2本以上で重なったり交わったりしてしまうような点を特異点と言います．正しくは，曲線の特異点は$x,y$での偏微分が互いに0となる点と定義します（より一般的にはヤコビ行列を用いる）．実際のところ，$X = V(x^3 - y^2)$について
$$
\frac{\partial f}{\partial x} = 3x^2, \frac{\partial f}{\partial y} = - 2y
$$
となるので
$$
3x^2 = - 2y = 0 \Rightarrow (x,y) = (0,0)
$$
となり，$(0,0) \in X$なので原点$(0,0)$は実際に$X$の特異点となっています．
曲線や曲面といった，方程式で表すことができる図形を一般化した概念を代数多様体と言いますが，それが特異点をもたないとき，その代数多様体は非特異(nonsingular)である，あるいは滑らか(smooth)であるといいます．
特異点解消
以下は発展的な内容を含みますので，特に興味のない方は読み飛ばしてください．
広中の定理から，標数0の体上の任意の代数多様体は非特異多様体と双有理同値になります．つまり，特異点を持つ曲線や曲面などは，(双)有理写像という特殊な写像で非特異なものに写すことができるということです．このような操作を特異点解消といいます．
一般の代数多様体はブローアップという操作を有限回行うことにより特異点を解消することができますが，今回は正規化という操作で特異点を解消してみたいと思います．
$A$を整域とし，$K(A)$をその商体とします．任意の$x \in K(A)$に対してある$a_i \in A$が存在して
$$
x^n + a_1 x^{n-1} + \cdots + a_{n-1} x + a_n = 0
$$
を満たす時，つまり$x$がある$A$係数モニック多項式の根になっている時，$x$は$A$上整であるといいます．このような$K(A)$の元をすべて集めてきた集合を整閉包(integral closure)といい$\overline{A}$と表しますが，これが$\overline{A} = A$となるとき，つまり整な元$x$を取ってくると必ず$A$に含まれるとき，$A$は整閉整域(integrally closed domain)と言います．
$X$のアフィン座標環である$A(X) = k[x,y]/(x^3 - y^2)$は整閉整域ではありません．$t = y/x \in K(A(X))$とすると
$$
t^2 = y^2/x^2 = x^3/x^2 = x
$$
となるので，$t^2 - x = 0$となるので$t$は$A(X)$上整な元となります．しかし，明らかに$t \not\in A(X)$なので，$A(X)$は整閉整域ではないことがわかります．
一般の代数多様体について，それが非特異であればその座標環は整閉整域になりますが，曲線の場合は特に非特異であることと座標環が整閉整域であることは同値になります．
ここで
$$\iota: A(X) \hookrightarrow A(X)[t]/(t^2 - x)$$
を考えます．すると右辺は
$$
\begin{array}{ccc}
A(X)[t]/(t^2 - x) & \rightleftarrows & k[t] \\
(x, y, t) & \mapsto & (t^2, t^3, t) \\
t & \leftarrowtail & t
\end{array}
$$
という同型射により$A(X)[t]/(t^2 - x) \simeq k[t]$であることがわかります．また，明らかに$k[t]$は整閉整域となっています．このような操作を（環の）正規化(normalization)といいます．
$k[t]$はアフィン直線$\aa^1$の座標環なので，$\aa^1$から$X$に逆向きに代数多様体の間の有理写像ができます:
$$
\begin{array}{cccc}
\phi: & \aa^1 & \dashrightarrow & X \\
& t & \mapsto & (t^2, t^3) \\
& y^2 / x & \leftarrowtail& (x, y)
\end{array}
$$
$\phi$の右向きは射となりますが，左向きは$x = 0$で定義されないので有理写像となりますが，これはちょうど双有理写像となっています．もちろん$\aa^1$は直線であり，特異点を持っていません．
以上の操作により，$X$と双有理同値で非特異な代数多様体(いまは直線)を構成することができました．このような操作を特異点解消といいます．
特異点解消は代数幾何学の主要なテーマであるだけでなく，超関数論や統計学と結びつくことにより，情報幾何や機械学習などさまざまな応用が研究されている[3]対象です．詳しい話は全然わかりませんが一説によると人間の脳の中には特異点があり，人間はその特異点をうまく解消しているんだとか．ワクワクしますね．
まとめ
今回は簡単な問題を通じて代数幾何学の一つの側面をざっと通して見てみました．代数幾何学とはこのように，「方程式や環・体」といった代数的構造と，「曲線や曲面あるいは空間」といった幾何的構造の対応関係を以て互いの性質を研究するという分野です．
これからも継続して記事を書いていきますので，もし興味があればMathlogおよびTwitterのフォローをよろしくお願い致します．